7. Мода и медиана. Средние величины
 Скачать 155 Kb.
|
|
Наряду с абсолютными и относительными величинами в статистике большое применение находят средние величины. В повседневной жизни употребляются термины "в среднем", "средняя". Например, средняя цена, средний расход продуктов, средняя заработная плата, средняя мощность оборудования, средняя выработка, средний размер сбережений и т. д. В экономическом анализе часто приходится оперировать средними величинами в целях лучшего понимания общей картины, когда нужно из многих признаков получить величину, в которой отражались бы свойства всех признаков, входящих в состав совокупности. Средняя величина в С - обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности. Средняя величина есть обобщающая количественная характеристика однородных явлений по какому-либо варьирующему признаку. Применение средних величин позволяет охарактеризовать определенный признак совокупности одним числом, несмотря на количественные различия единиц по данному признаку внутри совокупности. Следовательно, средняя величина есть обобщающая характеристика совокупности; средняя величина выражает типичное свойство совокупности; средняя величина — величина абстрактная, а не конкретная, так как в ней сглаживаются отдельные значения единиц совокупности, имеющие отклонения в ту и другую сторону; реальность средней величины достигается, если она вычисляется из одной совокупности. Пользуясь средними величинами при анализе массовых явлений, необходимо всегда помнить, что часто в средней величине скрываются отстающие хозяйствующие субъекты, которые имеют низкие показатели своей деятельности и, наоборот, не выявляются фирмы, компании, предприятия и т. д., которые работают весьма эффективно. Это возможно, как уже говорилось выше, в связи со свойством средней, в которой отклонения отдельных значений признака от ее величины взаимно погашаются. (Так, например, при условии выполнения плана розничного товарооборота в целом по холдингу, занимающемуся продажей товаров, часть фирм, входящих в него, не выполнила план и, наоборот, другая часть перевыполнила план товарооборота.) Поэтому, кроме средней, следует использовать и отдельные индивидуальные показатели работы фирм, входящих в холдинг. В эк. практике исп.-ся широкий круг показателей, вычисленных в виде средних величин. Напр, обобщающим показателем доходов рабочих АО служит средний доход одного рабочего, определяемый отношением фонда з/п и выплат социального характера за рассматриваемый период (год, квартал, месяц) к численности рабочих АО. Вычисление среднего – один из распространенных приемов обобщения; средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от колич. значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей. Там, где возникает потребность обобщения, расчет таких характеристик приводит к замене множества различных инд. значений признака средним показателем, характеризующим всю совокупность явлений, что позволяет выявить закономерности, присущие массовым общ. явлениям, незаметные в единичных явлениях. Средняя отражает характерный, типичный, реальный уровень изучаемых явлений, характеризует эти уровни и их изменения во времени и в пространстве; это сводная характеристика закономерностей процесса в тех условиях, в к-рых он протекает. Выбор вида средней определяется эк. содержанием определенного показателя и исходных данных. 1)- Класс степенных средних - арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д. Помимо степенных средних в с/практике используются 2) Структурные средние - применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.. Мода и медиана, расчет и применение в с/анализе. Квартили и децили Термин "мода" находит употребление в тех случаях, когда определяется наиболее часто встречающееся значение признака, иначе говоря, мода — это есть варианта, у которой частота (вес) наибольшая. Модальная величина в дискретном ряду находится просто — по наибольшей частоте. Пр:. Крупной обувной фабрикой "Буревестник" проведено выборочное обследование потребляемой женщинами обуви (табл. 7). Таблица .7 Данные выборочного обследования потребляемой женщинами обуви
Как видно из приведенного вариационного ряда, наиболее часто встречающейся величиной, т. е. модой этого ряда, является размер обуви 37, который носит 2696 женщин из опрошенных 9493 человек. Несколько сложнее определение моды в интервальном вариационном ряду (табл. .8). В этих случаях необходимо моду находить расчетным путем по формуле:  где хто— нижняя граница модального интервала (в приведенном примере она составляет 140 кв. м); i— разность между верхней и нижней границей модального интервала (в примере — 20 кв. м);  - частота интервала, предшествующая модальному (в примере 15 магазинов); - частота модального интервала (в примере 20 магазинов); - частота интервала, следующего за модальным (в примере— 8 магазинов).Пример. На основании группировочных данных о торговой площади магазинов произведем расчет моды из интервального ряда (табл.8). Таблица .8 Группированные данные по торговой площади магазинов
Как видно из сгруппированных данных, модальный интервал будет лежать в границах интервала от 140 до 160 кв. м, так как этому интервалу соответствует большая частота (20 магазинов). Теперь подставим числовые значения из приведенного примера в формулу 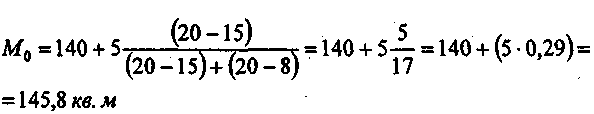 Следовательно, из этой группы больше всего магазинов имеют торговую площадь 145,8 кв. м. Как и мода, медиана относится к структурным средним, она так же является конкретной величиной. Размеры отклонений значений других вариант на моду и медиану не оказывают влияния. Медианой называется серединная варианта упорядоченного вариационного ряда, расположенного в возрастающем и убывающем порядке. Она является центральным членом и делит вариационный ряд пополам в тех случаях, если этот ряд нечетный. В ряду, состоящем из 15 чисел, медианой будет 8-е число, от которого как вниз, так и вверх будет расположено по 7 чисел. Например, в торговле эти две величины применяются при определении покупательского спроса на отдельные продовольственные и непродовольственные товары, при определении качества товаров и т. д. Пример. А. Дан нечетный вариационный ряд роста студенток: 156 158 160 [161] 166 168 172 Из приведенного нечетного ряда видно, что центральным членом (медианой) данного ряда является рост студентки — 161 см. В случае четного вариационного ряда медиана определяется следующим образом: серединные два члена вариационного ряда складываются и делятся пополам. Б. Дан четный вариационный ряд роста студенток: 155 156 158 160 161 166 168 172  Расчет медианы интервального ряда. Если варианты в ряду распределения заданы в виде интервалов, то первоначально находят медианный интервал, который содержит единицу, находящуюся в середине ранжированного ряда. Для определения этого интервала сумму частот делят пополам и на основе последовательного суммирования частот первого, второго, третьего и т. д. интервалов находят интервал, где расположена медиана. Приближенное значение Ме в медианном интервале исчисляется по формуле: 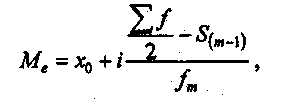 где хо— нижняя граница медианного интервала; i— величина медианного интервала;  — сумма частот интервального ряда;S(m-1)— сумма накопленных частот в интервалах предшествующих медианному; fт— частота медианного интервала. Из этой формулы следует, что к нижней границе медианного интервала (хо) добавляется та часть медианного интервала, которая пропорциональна удельному весу в частоте медианного интервала части ее, расположенной от нижней границы интервала до Ме. Пример. В интервальном ряду (табл. 9) даны группы семей по среднемесячному доходу на 1 человека. Требуется определить для этого ряда серединное значение, т. е. медиану. Таблица .9 Расчет медианы по интервальному ряду
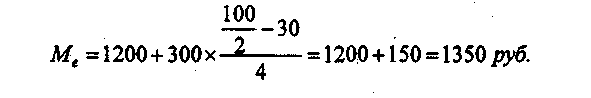 Следовательно, 50% семей имеют доход на одного человека не более 1350 руб., а 50% имеют доход на одного человека более 1350 руб. У медианы есть свойство, которое заключается в том, что сумма абсолютных величин линейных отклонений от Меминимальна.  Это свойство очень важно при практическом применении медианы.Пример. Филиалы торговой фирмы "Элегант" расположены на расстоянии 10,30, 70,90,100 км от нее. Где построить склад фирмы для оптимального снабжения филиалов? Расчет показан в табл. .10. Таблица .10 Расчетная таблица для сравнения отклонений от медианы и от средней арифметической
 ; Ме= 70 км.Таким образом, оптимальным вариантом является медианное расстояние 70 км, так как 150 < 160 км на 10 км. Подводя итог рассмотрению моды и медианы особо следует отметить, что данные два показателя часто используются вместо средней арифметической или вместе с ней. Так, например, фиксируя цены на продукты на мелкооптовых рынках, записывают наиболее часто встречающуюся цену каждого продукта, т. е. моду цены. Однако наилучшей характеристикой величины варианта или уровня ряда служит средняя арифметическая, которая имеет ряд преимуществ, главное из них — точное отражение суммы всех значений признаков, необходимой для решения ряда практических задач. Вместе с тем для тех случаев, когда в совокупности имеется небольшое число единиц с чрезмерно большим или чрезмерно малым значением исследуемого признака, в дополнение к средней арифметической целесообразно исчислять моду и особенно медиану, которые, в отличие от средней, не зависят от этих крайних, не характерных для совокупности значений признаков. Мода (Мо) – значение случайной величины, встречающееся с наибольшей вероятностью, в дискретном вариационном ряду – вариант, имеющий наибольшую частоту. Например, в табл..1 наибольшей частотой является число 5. Этой частоте соответствует модальное значение признака, т.е. выработка деталей за смену. Мода свидетельствует, что в данном примере чаще всего встречаются рабочие, изготавливающие за смену 20 деталей. В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:  ( )где – нижняя граница модального интервала; – модальный интервал; – частоты в модальном, предыдущем и следующем за модальным интервалах (соответственно). Модальный интервал определяется по наибольшей частоте. По данным табл. 4.4 рассчитаем моду, тыс. руб.:  Итак, модальным значением стоимости ОПФ малых предприятий региона является стоимость, равная 18,33 тыс. руб. Мода широко используется в с/практике при изучении покупательского спроса, регистрации цен и т.п. Медиана (Ме) – это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану необходимо отыскать значение признака, которое находится в середине упорядоченного ряда. В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы. Пусть ряд состоит из показателей заработной платы 9 рабочих (руб. в месяц ) в 2000 г.: 630, 650, 680, 690, 700, 710, 720, 730, 750. Номер медианы для нечетного объема вычисляется по формуле  где n – число членов ряда.В нашем примере номер медианы равен 5, медиана равна 700 руб. (т.е. одна половина рабочих получила зарплату менее 700 руб., а другая – более 700 руб. в месяц). В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда. В интервальных рядах распределения медианное значение (поскольку оно делит всю совокупность на две равные по численности части) оказывается в каком-то из интервалов признака х. Этот интервал характерен тем, что его кумулятивная частота (накопленная сумма частот) равна или превышает полусумму всех частот ряда. Значение медианы вычисляется линейной интерполяцией по формуле:  (13)где – нижняя граница медианного интервала; - медианный интервал; – половина от общего числа наблюдений; – сумма наблюдений, накопленная до начала медианного интервала; – число наблюдений в медианном интервале. Формула (13) получена исходя из допущения о равномерности нарастания накоплений частоты внутри интервала и пригодна для любого интервального ряда. Рассчитаем медиану по данным табл. 4.4. Прежде всего найдем медианный интервал. Таким интервалом очевидно будет интервал стоимости ОПФ малых предприятий (18–20 тыс. руб.), поскольку его кумулятивная частота равна 18 (2+6+10), что превышает половину суммы всех частот (25:2 = 12,5). Нижняя граница интервала 18 млн руб., его частота 10; частота, накопленная до него, равна 8. Подставив данные в формулу (4.13), получим, тыс. руб.:  Полученный результат говорит о том, что из 25 малых предприятий региона 12 предприятий имеют стоимость ОПФ менее 18 тыс. руб., а 12 предприятий – более этой величины. Медиана находит практическое применение в маркетинговой деятельности вследствие особого свойства – сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая: . Мода и медиана в отличие от степенных средних являются конкретными характеристиками, их значение имеет какой-либо конкретный вариант в вариационном ряду. Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить асимметрию ряда распределения. Мода и медиана, как правило, являются дополнительными к средней характеристиками совокупности и используются в математической статистике для анализа формы рядов распределения. Квартили и децили Более общая постановка вариант, занимающих определенное порядковое место в ранжированном ряду, называется порядковой статистикой. К порядковым статистикам принадлежат и экстремальные значения признака, т. е. минимальные и максимальные в данном ряду. Различают порядковые статистики, отсекающие четверти совокупности, которые называются квартили; первую или нижнюю (отсекающие четверть совокупности снизу), третью или верхнюю (отсекающие четверть сверху). Второй квартилью можно назвать медиану. Далее можно говорить об отсекающих десятые части — децилях и т. д. Определение этих порядковых статистик в вариационном ряду, так же как и определение медианы, начинается с расчета порядкового номера соответствующего варианта, а затем по накопленным частотам определяется интервал, в котором находится соответствующий вариант. Определение величины накопленного варианта внутри интервала тоже аналогично нахождению медианы. В интервальном вариационном ряду квартили внутри определенного по накопленным частотам интервала рассчитываются по следующим формулам: Нижний квартиль Верхний квартиль 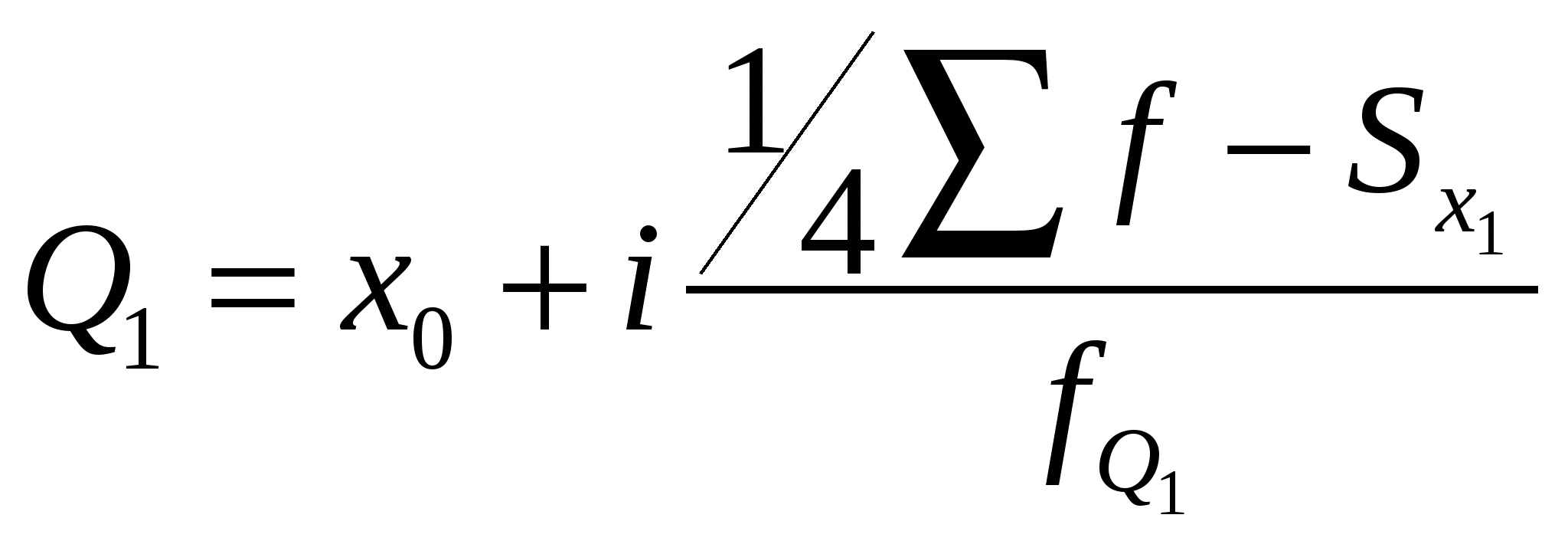 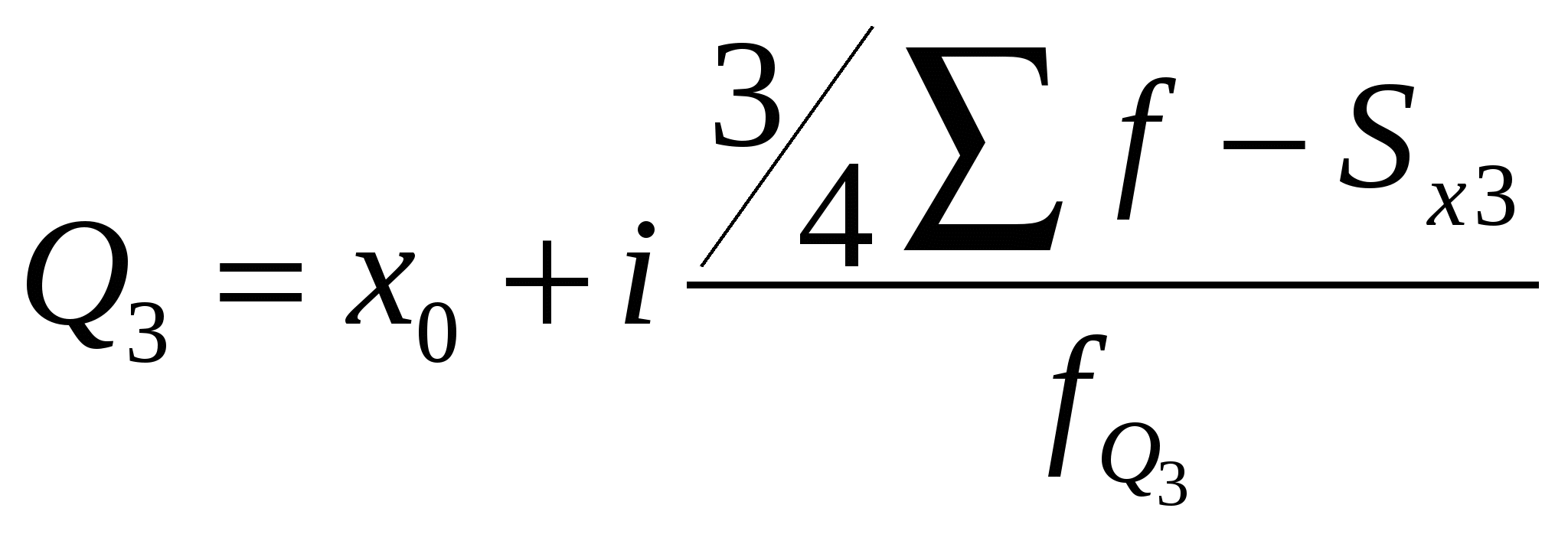 где хо — нижняя граница квартальных интервалов; i— величина интервала; — сумма частот;  — накопленная частота интервала, предшествующего нижнему квартилю; — накопленная частота интервала, предшествующего верхнему квартилю; — частоты квартального интервала.Формулы для децилей в интервальном вариационном ряду записываются следующим образом: 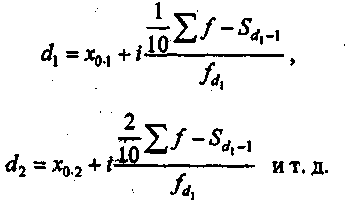 Пример. В табл. 11 дан интервальный ряд распределения 50 учащихся по росту. Определить верхний и нижний квартиль и первые два дециля. Таблица .11 Распределение 50 учащихся по росту в интервальном ряду
 |
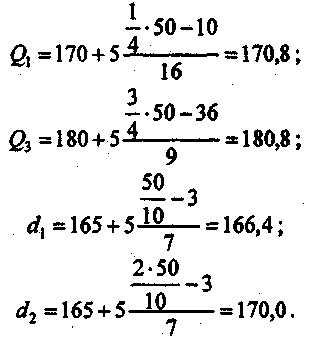