Контрольная работа электродинамика. 6. Возбуждение прямоугольного резонатора. Возбуждение круглого цилиндрического резонатора

• Название: 6. Возбуждение прямоугольного резонатора. Возбуждение круглого цилиндрического резонатора
• Анкор: Контрольная работа электродинамика
• Дата: 24.05.2022
• Размер: 1.31 Mb.
• Имя файла: 06.doc
• Тип: Документы; #546926
• страница: 2 из 3

Задание 2
Комплексные амплитуды векторов электромагнитного поля в некоторой точке пространства задаются выражениями



Частота колебаний равна f.

1). Найти мгновенное значение вектора в момент времени равный t.

2). Вычислить плотность тока смещения в этой точке.

3). Определить комплексный вектор Пойнтинга и его среднее значение.

Таблица выбора исходных данных для выражений и .

Последняя цифра номера зачетной книжки	A	B	C	α	β	γ
0	0,85	1,3	4,2·10-3	0,6	-0,7	-1,2
1	1,5	2,1	0,45	1,1	-1,4	3,5
2	3,7·10-1	0,94	7,9	5,8	9,0	2,5
3	8,9	2·10-3	4,1	4,8	3,9	0,1
4	-7,2	1,2	9,3	2,4	5,9·10-2	1,4
5	4,2	-3,8	6,9	4,1·10-3	8,8	3,5·10-3
6	2,1	3,9	4,6	1,8	9,1	2,7
7	2	8,2	1,8	3,9	0,3	-0,2
8	6,7	12,1	8,9	8,9	-1,7	-0,3
9	8,3	-1,2	8,9	2,3	-0,5	-0,8

Таблица выбора исходных данных для значения времени и частоты

Последняя цифра номера зачетной книжки	0	1	2	3	4	5	6	7	8	9
t, мкс	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
f, MГц	1	2	3	4	5	6	7	8	9	10

Вариант 6: А = 2,1; В = 3,9; С = 4,6;  = 1,8;  = 9,1;  = 2,7; t = 0,7 мкс;
f = 7 МГц.

Тогда комплексные амплитуды векторов электромагнитного поля в некоторой точке пространства будут описываться соотношениями




1). Определим мгновенное значение вектора в момент времени равный t = 0,7 мкс.



















В момент времени равный t = 0,7 мкс мгновенное значение вектора









Таким образом, получено





2). Вычислим плотность тока смещения в этой точке.

Плотность тока смещения в пространстве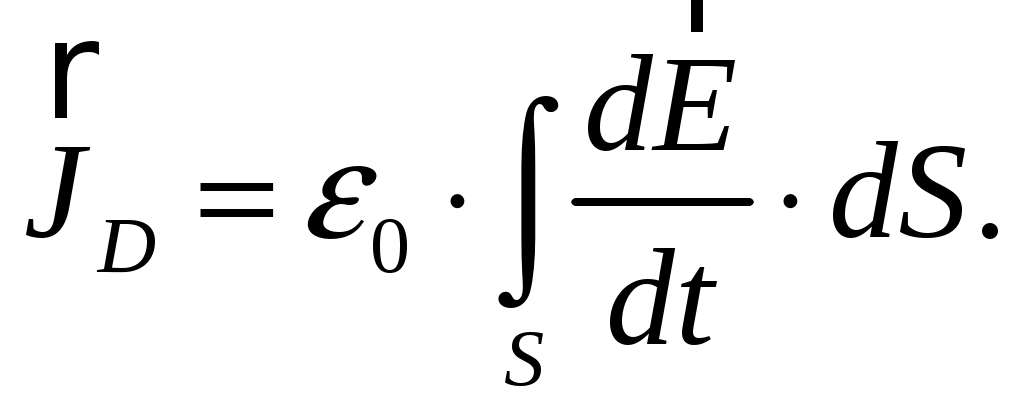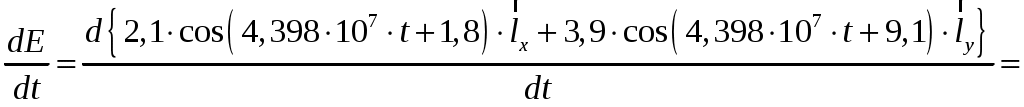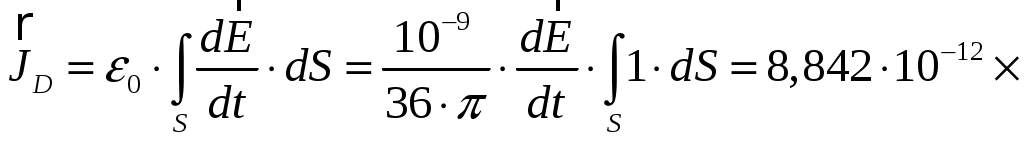

























В момент времени равный t = 0,7 мкс плотность тока смещения в этой точке











Таким образом, получено







3). Определим комплексный вектор Пойнтинга и его среднее значение.

Комплексный вектор Пойнтинга определяется как векторное произведение векторов электрической и магнитной напряженностей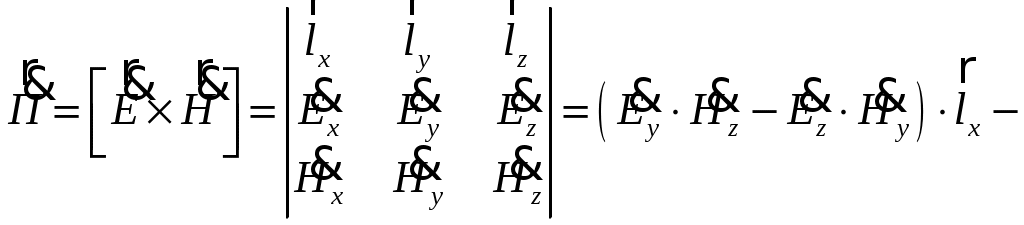





С учетом того, что E_z = 0; H_x = H_y = 0 имеем



По варианту задания было получено









Средняя плотность комплексного вектора Пойнтинга [1, стр. 176]

















Среднее значение комплексного вектора Пойнтинга


Выводы. Если комплексные амплитуды векторов электромагнитного поля в некоторой точке пространства задаются выражениями



при частоте колебаний f = 7 МГц, то

1) мгновенное значение вектора в момент времени равный t = 0,7 мкс





2) плотность тока смещения в этой точке





3) комплексный вектор Пойнтинга



вектор среднего значения



и его среднее значение



Задание 3
По проводникам коаксиального волновода (см) протекает постоянный ток I. Проводники коаксиального волновода выполнены из меди. Пространство между внутренним и внешним проводниками заполнено полиэтиленом. При решении задачи считать, что в каждый момент времени токи во внешнем и внутреннем проводниках в одном поперечном сечении противоположны и равномерно распределены по поперечным сечениям проводников.

1). Вывести закон, выражающий зависимость напряженности магнитного поля от расстояния от центра коаксиального волновода. Построить график зависимости.

2). Найти векторы напряженности магнитного поля и магнитной индукции на расстояниях r₁ = 0,5 R₁; r₂ = (R₁ + R₂)/2; r₃ = (R₂ + R₃)/2; r₄ = 2R₃.

Таблица для выбора исходных данных для задания 3

Последняя цифра номера зачетной книжки	0	1	2	3	4	5	6	7	8	9
R1, мм	2	1	3	4	6	9	2	4	1	2
R2, мм	7	5	8	9	18	25	5	10	4	6
R3, мм	8	7	9	10	19	26	6	11	5	7

Таблица для выбора исходных данных для задания 3

Последняя цифра номера зачетной книжки	0	1	2	3	4	5	6	7	8	9
I, мА	8	5	6	5	9	15	7	8	3	5

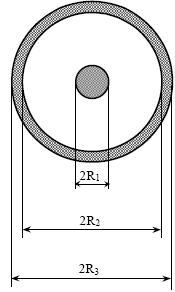Рисунок 3.1

Вариант 6: R₁ = 2 мм;R₂ = 5 мм;R₃ = 6 мм; I = 7 мА.

Ток, протекающий по внутреннему проводу коаксиального кабеля равен I = 7 мА, тогда ток внешнего проводника  минус 7 мА [1, стр. 126 - 127].

Распределение тока по сечениям проводников будем считать равномерным. Для определения магнитного поля внутри провода выберем в качестве контура окружность радиуса r < R₁. Учитывая, что ток, охватываемый контуром в этом случае равен I/(r/R₁)², получаем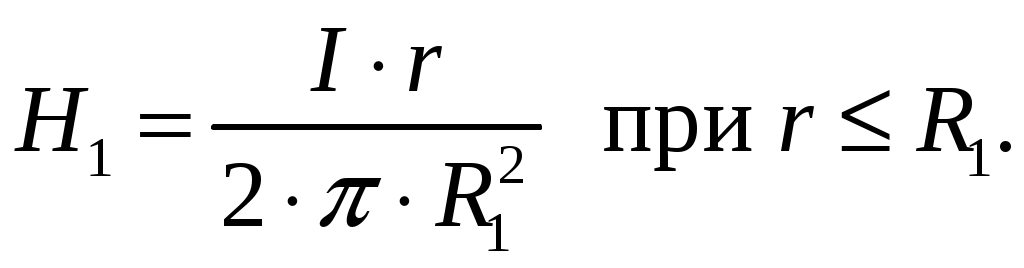



Для значений радиуса r от R₁ до R₂ магнитное поле изменяется по закону [1, стр. 126, формула (4.44)]



Для значений радиуса r от R₂ до R₃ магнитное поле изменяется по закону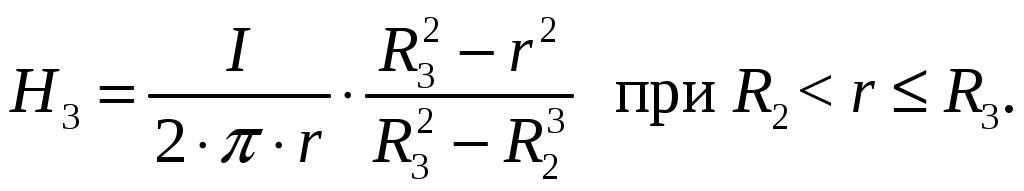



Для значений радиуса r больше R₃ магнитное поле равно нулю.

График изменения амплитуды магнитного поля при изменении радиуса от нуля до 8 мм построим в программе MathCad 15 (рис. 3.2).

На рис. 3.3 построено совмещенное изменение графика амплитуды магнитного поля с конструкцией коаксиального кабеля.



Рисунок 3.2


Н, А/м


r, м


Окончание рисунка 3.2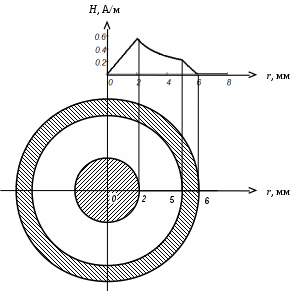



Рисунок 3.3