Контрольная работа электродинамика. 6. Возбуждение прямоугольного резонатора. Возбуждение круглого цилиндрического резонатора
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
Задание 4 В волноводе прямоугольного сечения распространяется волна основного типа. Амплитуда напряженности электрического поля. Амплитуда напряженности электрического поля равна Em. Стенки волновода выполнены из материала, указанного в таблице вариантов. Требуется: 1) определить частотные границы одноволнового режима; 2) определить частоту fmin, соответствующую минимальному коэффициенту ослабления αmin в заданном волноводе; 3) для частоты, соответствующей f = 1,5· 4) изобразить структуру поля в волноводе в продольном и поперечном сечении; 5) какие типы волн могут распространяться в данном прямоугольном волноводе, на частоте f = 1,5·t· Таблица выбора исходных данных для задания 4
Таблица выбора исходных данных для задания 4
Вариант 6: ширина волновода a = 22,86 мм; высота волновода b = 10,16 мм; Em = 60 кВ/м; материал стенок медь; t = 1,55. 1). Определим частотные границы одноволнового режима. Основная волна прямоугольного волновода Н10, ее КР = КР Н10 = 2а [1, стр. 281]. распространение этой волны возможно при < 2а или а > /2. Чтобы другие типы волн не могли распространяться достаточно потребовать, чтобы не могли распространяться волны Н20 и Н01. Для этого должны выполняться неравенства > КР Н20 и > КР Н01 или > а и > 2b. таким образом, одноволновый режим выполняется при /2 < а < и b < /2. Тогда получаем a < < 2а и > 2b. Таким образом, границы длин волн для одноволнового режима min = max{a; 2b}; max = 2a. min = max{a; 2b} = max{22,86 мм; 210,16 мм} = 22,86 мм; max = 2a = 222,86 = 45,72 мм. Частотные границы одноволнового режима будут определяться по формулам fmin = c/max = 3108/(45,7210-3) 6,562109 Гц = 6,562 ГГц; fmax = c/min = 3108/(22,8610-3) 1,3121010 Гц = 13,12 ГГц. 2). Определим частоту fmin, соответствующую минимальному коэффициенту ослабления αmin в заданном волноводе. Для волны основного типа Н10 коэффициент ослабления вычисляется по соотношению [3, стр. 98] 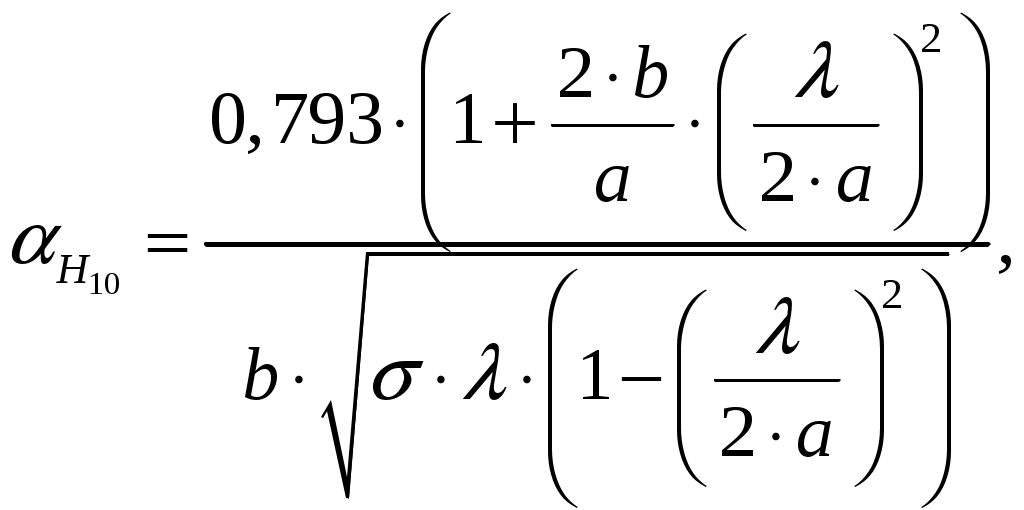 где a b сечение прямоугольного волновода, a b = 22,86 10,16 мм; проводимость металла стенок волновода, для меди [3, стр. 99] = = 4,57107 Сим/м. Для определения частоты, соответствующей минимальному коэффициенту ослабления построим график его зависимости от частоты в границах одноволнового режима (рис. 4.1).   f, Гц  , дБ/м Рисунок 4.1 При увеличении частоты величина затухания уменьшается. На частоте fmin = 15,6 ГГц достигается минимальное значение затухания min = 0,106 дБ. Монотонное возрастание затухания на частотах выше 15,6 ГГц обусловлено увеличением поверхностного сопротивления металла с ростом частоты [1, стр. 283]. 3). Для частоты, соответствующей f = 1,5· Критическая длина волны для волны основного типа Н10 в прямоугольном волноводе сечением a b = 22,86 10,16 мм КР Н10 = 2а = 222,86 = 45,72 мм. fКР Н10 = с/КР Н10 = 3108/(45,7210-3) 6,562109 Гц = 6,562 ГГц. f = 1,5· = с/f = 3108/(9,843109) 0,03048 м = 30,48 мм Фазовая скорость для волны основного типа Н10 в прямоугольном волноводе сечением a b = 22,86 10,16 мм [1, стр. 277] 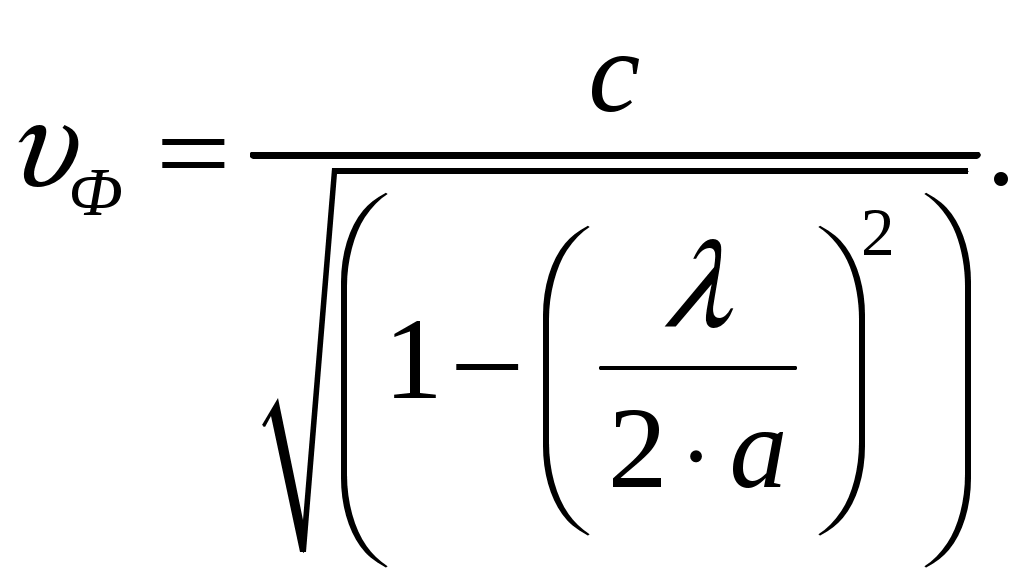 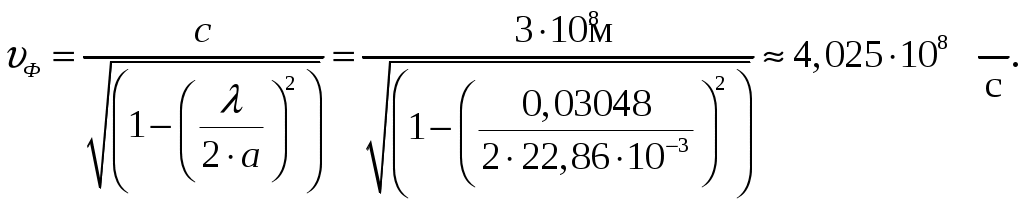 Групповая скорость [1, стр. 277] 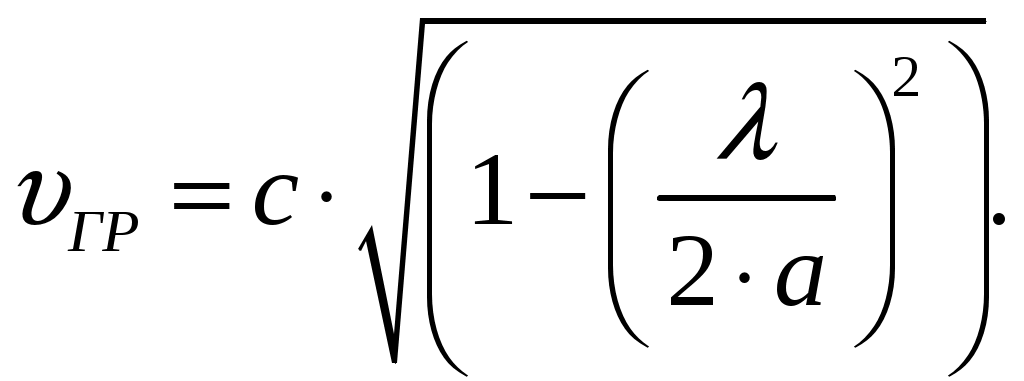 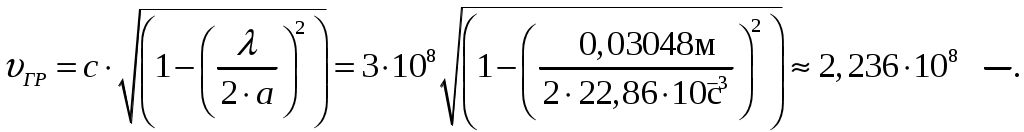 4). Изобразим структуру поля в волноводе в продольном и поперечном сечении. Полагаем f = 9,843 ГГц; 0,03048 м. Для волны Н10 справедливы соотношения [2, стр. 240] 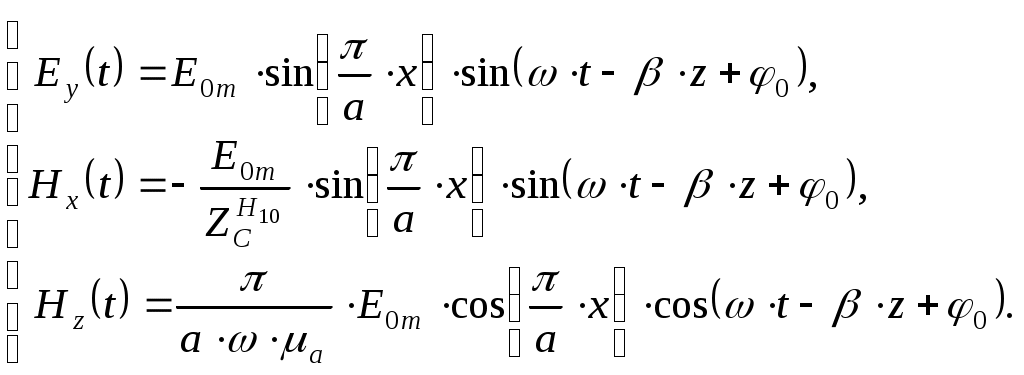 E0m = 60 кВ/м; /a = /0,02286 137,43 м-1; = 2f = 29,843109 6,1851010 Гц; 0 = 0рад. Коэффициент фазы 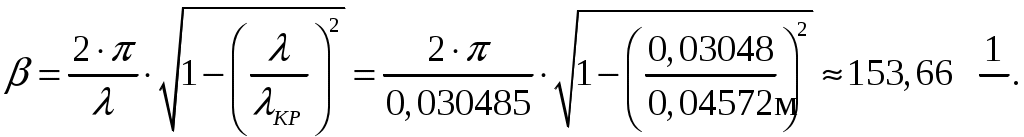 рад/м. рад/м.Волновое сопротивление 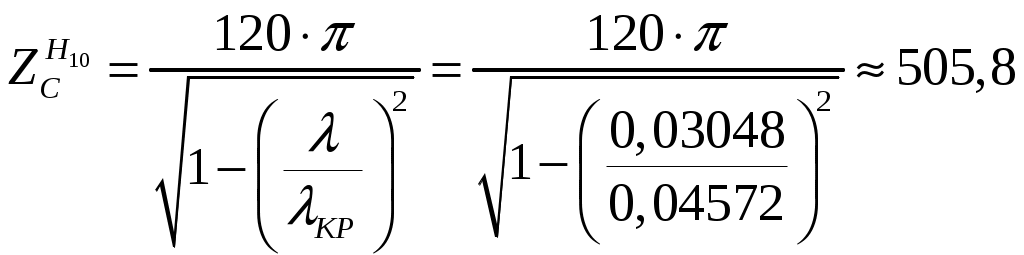 Ом. Ом.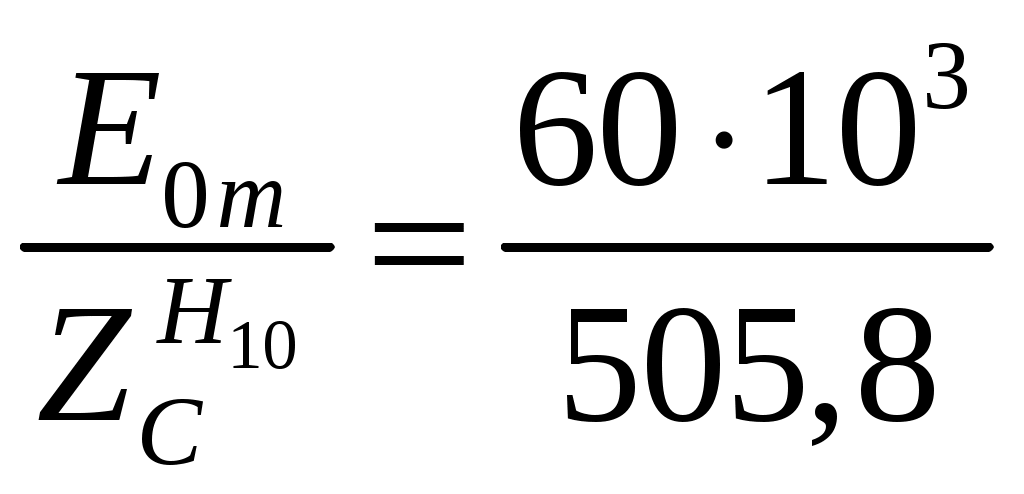 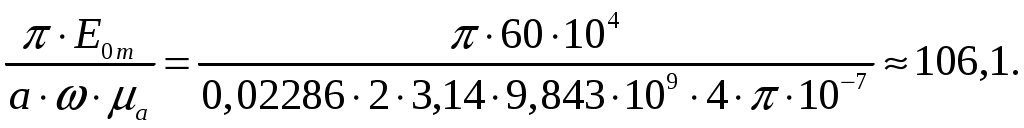 Тогда в численном виде можно записать 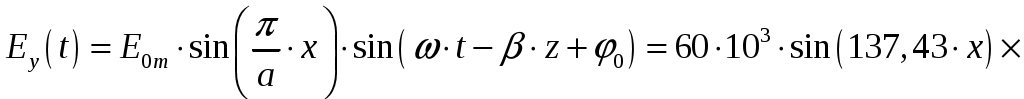 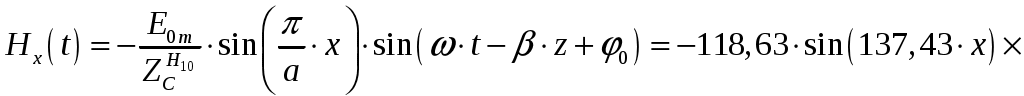 Выражения всех компонент поля волны Н10для фиксированного момента времени t = t1, определяемого условием t1 + 0 = 2принимают вид [1, стр. 240]: 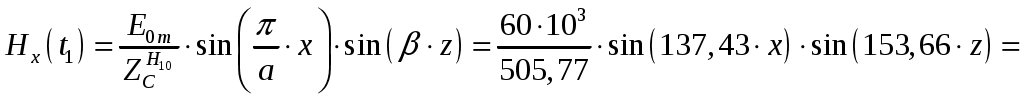 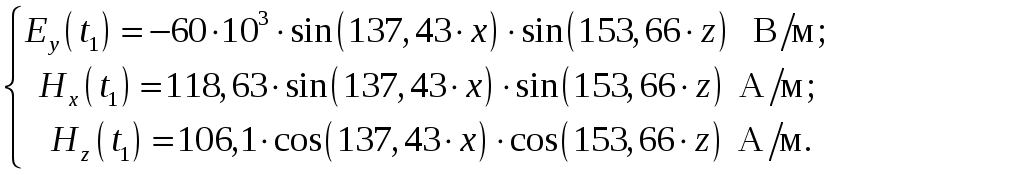 Из составленных выражений видно, что вектор Длина волны в волноводе 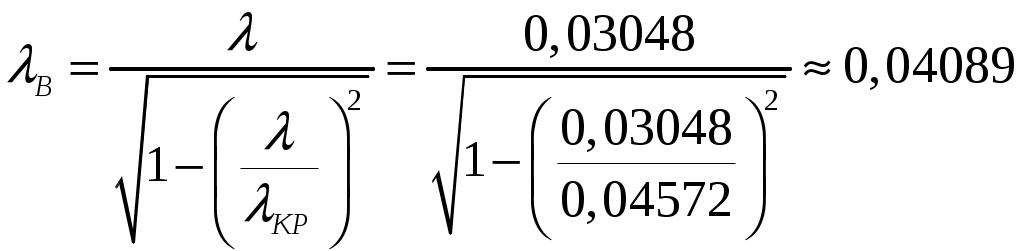 м. м.Рассмотрим структуру поля в момент времени t1 на отрезке волновода - B/4 z B/4, равном B/2. В различных поперечных сечениях (z = const) и продольных (x = const, y = const) сечениях формулы (2.13) принимают вид: при z =  при z = 0 м: 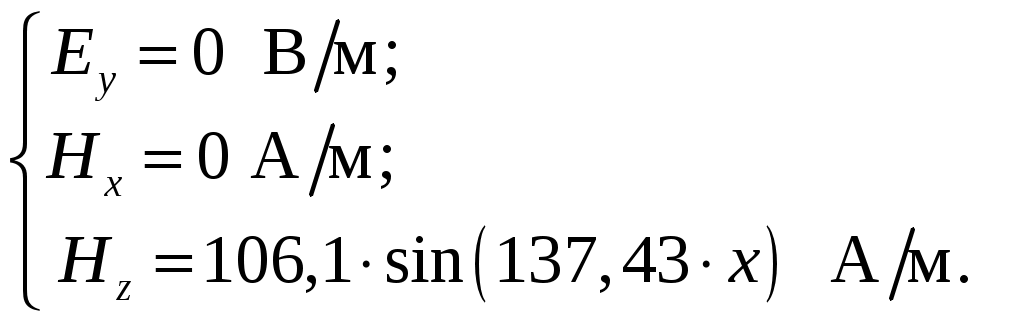 При x = a/2 = 0,02286/2 = 0,01143 м: 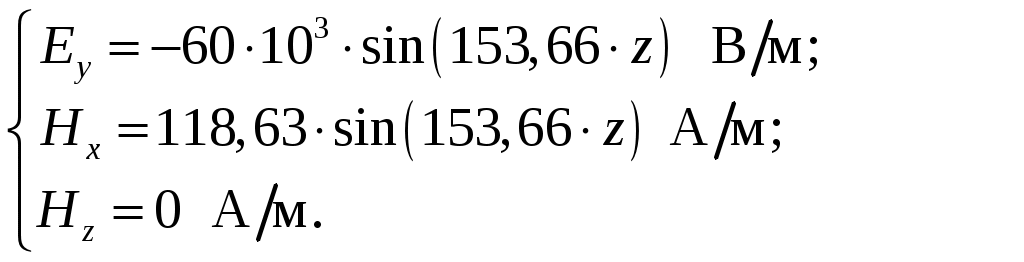 При y = const (0 y b = 0,01016 м): 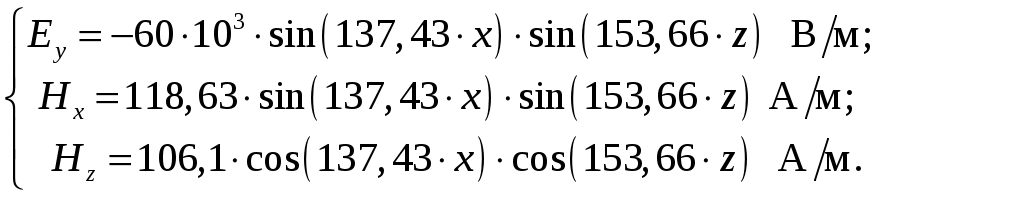 На рис. 4.2 для поля H10 построены распределения векторных линий   а) б) Рисунок 4.2 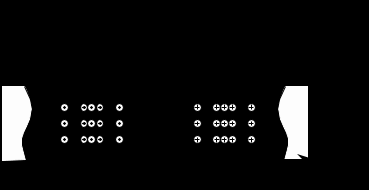 в) 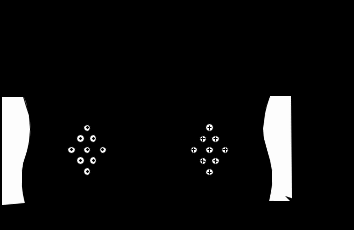 г) Окончание рисунка 4.2 С течением времени картины векторных линий (см. рис. 4.2) перемещаются со скоростью Ф = 5). Определим какие типы волн могут распространяться в данном прямоугольном волноводе, на частоте f = 1,5·t· f = 1,5·t· = с/f = 3108/(15,26109) 0,01967 м = 19,67 мм. Для существования волны заданного колебания необходимо выполнение условия [4, стр. 140] 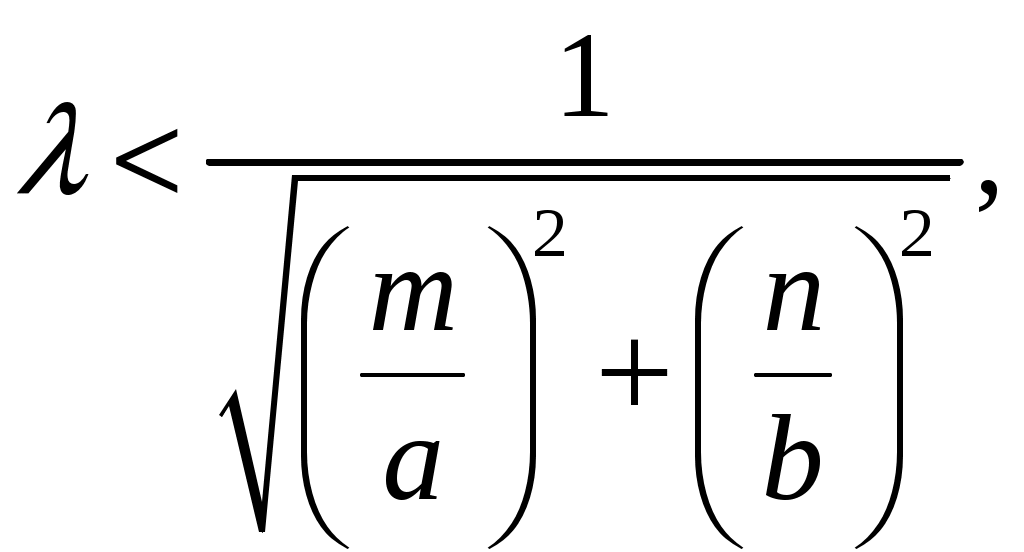 где m и n индексы колебания; a b поперечное сечение прямоугольного волновода, a b = 22,86 10,16 мм. Н10: m = 1, n = 0. 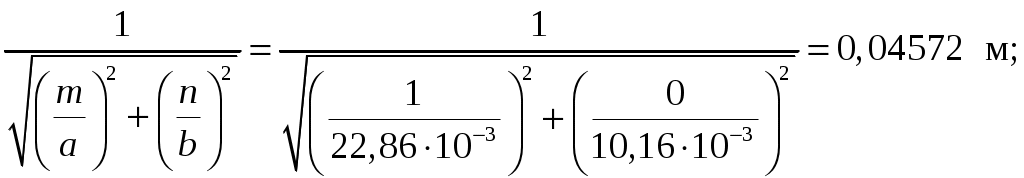 Условие выполняется, колебание Н10 будет существовать. Н01: m = 0, n = 1. 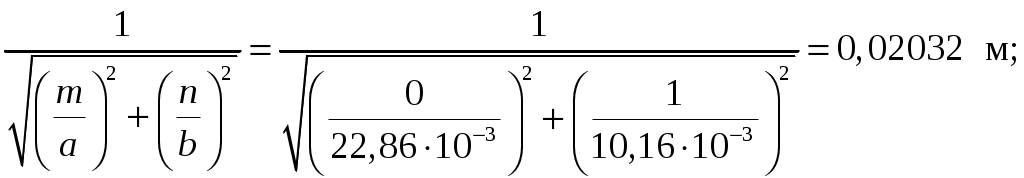 Условие выполняется, колебание Н01 будет существовать. Н20: m = 2, n = 0. 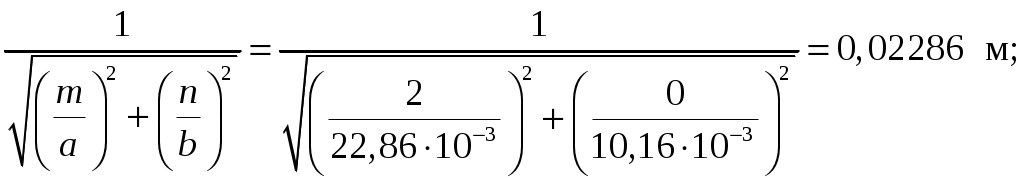 Условие выполняется, колебание Н20 будет существовать. Н02: m = 0, n = 2. 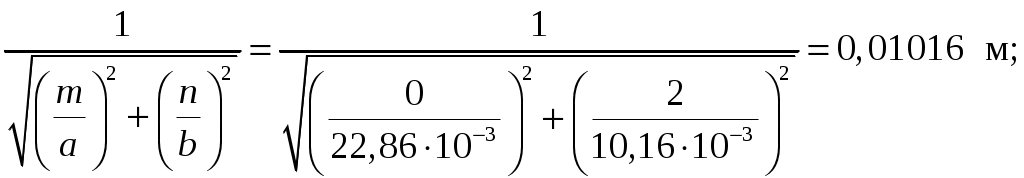 Условие не выполняется, колебание Н02 существовать не будет. Колебания Н03, Н04 и т. д. будут иметь критические длины волн меньше 0,01016 м и существовать не будут. Н30: m = 3, n = 0. 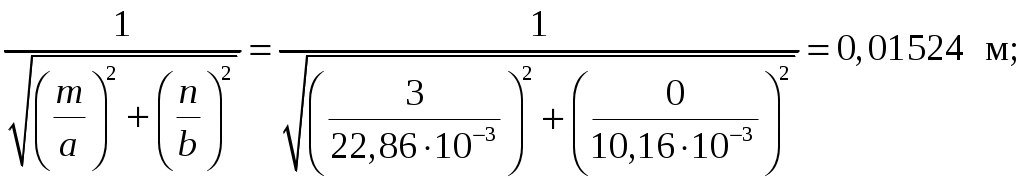 Условие не выполняется, колебание Н30 существовать не будет. Колебания Н40, Н50 и т. д. будут иметь критические длины волн меньше 0,01524 м и существовать не будут. Н11, E11: m = 1, n = 1. 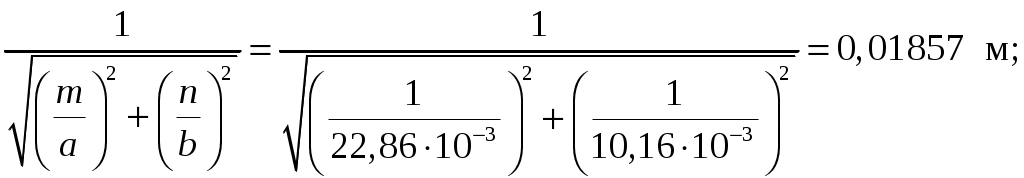 Условие не выполняется, колебания Н11 , Е11 существовать не будут. Колебания Н21, Е21, Н12, Е12, Н22, Е22 и т. д. будут иметь критические длины волн меньше 0,01857 м и существовать не будут. Таким образом, в прямоугольном волноводе сечением 22,86 10,16 мм на частоте f = 15,26 ГГц могут распространяться волны типа: Н10, Н01 и Н20. Список литературы 1. Пименов, Ю. В. Техническая электродинамика / Пименов Ю. В., Вольман В. И., Муравцов А. Д. Под ред. Ю. В. Пименова: Учеб. пособие для вузов. М.: Радио и связь, 2000. – 536 с.: ил. 2. Фальковский, О. И. Техническая электродинамика: Учебник. 2-е изд., стер. СПб.: Издательство «Лань», 2009. 432 с.: ил. 3. Фельдштейн, А. Л. Справочник по элементам волноводной техники. Изд. 2-е, перераб. и доп. / А. Л, Фельдштейн, Л. Р. Явич, В. П. Смирнов. М.: Советское радио, 1967. 652 с.: ил. 4. Федоров, Н. Н. Основы электродинамики: Учебное пособие для вузов / Н. Н. Федоров. М.: Высшая школа, 1980. 399 с.: ил. |
