Алфавит. 8 Радиопередатчики с угловой модуляцией 1 Общие сведения об угловой модуляции
 Скачать 298.52 Kb.
|
|
8 Радиопередатчики с угловой модуляцией 8.1 Общие сведения об угловой модуляции При изучении амплитудной модуляции в разделе 6, передача информации осуществлялась путём изменения амплитуды несущего колебания в соответствии с передаваемым сигналом. Представим теперь несущее колебание в следующем виде u(t)=Ucos(ωt+φ)= UcosФ(t) (8.1) Очевидно, что в соответствии с передаваемой информацией, помимо амплитуды, можно менять частоту ω или фазу φ, осуществляя, таким образом, частотную или фазовую модуляцию (ЧМ, ФМ). Согласно (8.1) в обоих случаях будет меняться угловой аргумент косинуса Ф(t), поэтому частотную и фазовую модуляцию объединяют общим термином «угловая модуляция». Тем не менее, как будет показано ниже, между ЧМ и ФМ есть и существенные различия. Воспользуемся простейшей моделью информационного сигнала в форме (6.1). Тогда колебание с частотной модуляцией можно представить в следующем виде u(t)=Ucos[(ω+ΔωcosΩt)t+φо] (8.2) В этом выражении Δω – амплитуда отклонения частоты при ЧМ, получившая название – девиация частоты; φо – произвольная постоянная, соответствующая фазовому сдвигу при t = 0. Согласно (6.1) и (8.1) Δω=Кчм·UΩ(8.3) Здесь Кчм - крутизна характеристики частотного модулятора. Аналогично для фазовой модуляции получим u(t)=Ucos(ωt+ΨcosΩt+φο) (8.4) В этом выражении Ψ – амплитуда отклонения фазы, названная индексом модуляции. По аналогии с (8.3) Ψ=Кфм·UΩ(8.5) Где Кфм - крутизна характеристики фазового модулятора. Частота и фаза гармонического колебания связаны следующими соотношениями 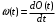 (8.6) (8.7)Используя эти зависимости можно определить связь между ЧМ и ФМ. Подставив значение Ф(t) из (8.4) в (8.6), определим как изменяется частота при ФМ 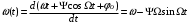 (8.8)Сравнивая частоту в выражениях (8.2) и (8.8), с учётом (8.5), получим Δω(ФМ) = ΨΩ = Ω·Кфм·UΩ(8.9) Таким образом, девиация частоты при ФМ пропорциональна амплитуде информационного сигнала и его частоте, в отличие от (8.3). Поэтому, в информационном сигнале, переданном фазовой модуляцией и принятым частотным детектором, произойдёт подъём верхних частот (исказится амплитудно-частотная характеристика). Подставим теперь частоту из (8.2) в (8.7) и определим как меняется фаза при ЧМ . 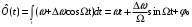 (8.10)Сравнивая фазу в (8.4) с (8.10), с учётом (8.3), получим  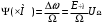 (8.11)В этом случае, индекс модуляции при ЧМ пропорционален амплитуде информационного сигнала и обратно пропорционален его частоте, в отличие от (8.5). Поэтому, в информационном сигнале, переданном частотной модуляцией и принятом фазовым детектором, произойдёт завал верхних частот. Рассмотренные отличия проявляются только в случае реальных информационных сигналов с меняющейся частотой Ω. Для его модели (6.1) с постоянной частотой, различие между ЧМ и ФМ полностью отсутствует. На основании (8.9) и (8.11) возможно взаимное преобразование ЧМ в ФМ и наоборот, обеспечив необходимую зависимость (или независимость) индекса модуляции от частоты модулирующего сигнала. В частности, для преобразования ФМ в ЧМ, необходимо амплитуду модулирующего сигнала изменять обратно пропорционально его частоте. Это может быть выполнено с помощью интегрирующей RC цепи, через которую перед модуляцией должен быть пропущен модулирующий сигнал (см. рисунок 8.1а).  Рисунок 8.1 – Преобразование видов угловой модуляции Действительно, коэффициент передачи такой цепи 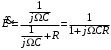 . При условии R>>ΩмаксС (8.12)Аналогично при использовании дифференцирующей цепи на входе частотного модулятора можно получить фазовую модуляцию (см. рис. 9.1б). 8.2 Спектр сигнала с угловой модуляцией Для анализа спектра сигнала с угловой модуляцией, воспользуемся выражением (9.4), положив φο=0. Сигнал такого вида раскладывается в ряд Фурье по функциям Бесселя следующим образом  (8.13)Здесь Jn(Ψ) – функция Бесселя первого рода n – го порядка, аргументом которой является индекс модуляции Ψ. Согласно (8.13), спектр сигнала с угловой модуляцией теоретически бесконечен . Форма огибающей спектра определяется зависимостью функций Бесселя от индекса модуляции. Графики первых четырёх функций Бесселя представлены на рисунке 8.2. Особенностью этих функций является затухающий колебательный характер, поэтому при некоторых значениях Ψ, указанных на рисунке 8.2, несущая частота (Jo) исчезает. В связи с этим, термин «несущая», при рассмотрении угловой модуляции, заменяют термином «средняя частота». Первый максимум функций Бесселя, начиная с n=1 , соответствует Ψ=n+1.  Рисунок 8.1 – Функции Бесселя Затухающий характер функций Бесселя позволяет на практике без последствий ограничивать полосу занимаемых частот на уровне составляющих, амплитуда которых не превышает 1% от немодулированной несущей. Эффективную полосу сигнала с угловой модуляцией в этом случае определяют эмпирической формулой  (8.14)В последнем выражении Fмакс – максимальная частота модулирующего сигнала. На рисунке 8.3 в качестве примера представлены спектры для некоторых значений Ψ[9]. 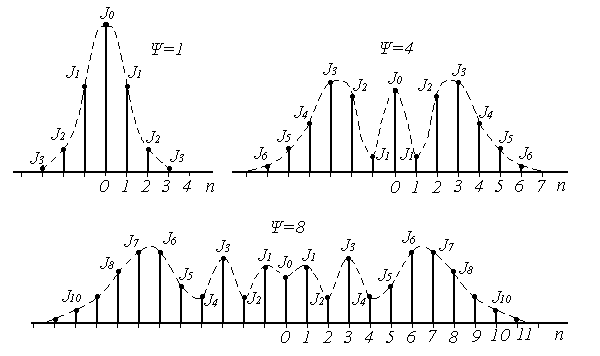 Рисунок 8.3 – Спектры сигналов с угловой модуляцией. Как уже отмечалось выше, при угловой модуляции одним гармоническим тоном, различия между ФМ и ЧМ нет, т.к индекс модуляции в этом случае величина постоянная. Иначе обстоит дело при модуляции сложным многочастотным сигналом. Поясним это на следующем примере. Пусть фазовая модуляция осуществляется двух тоновым сигналом, в котором одна частота (Ω1) очень низкая, а вторая (Ω2) во много раз выше первой. Поскольку при ФМ индекс модуляции не зависит от модулирующей частоты, спектры для обеих модулирующих частот будут подобны (см. рис. 8.4а). Предположим теперь, что при частотной модуляции на нижней частоте Ω1 индекс модуляции такой же, как при ФМ. Тогда на верхней частоте, согласно (8.11), индекс модуляции будет во много раз меньше, и, следовательно, эффективная полоса, при частоте модуляции Ω2,значительно сократится. Спектр сигнала с ЧМ для этого случая представлен на рисунке 8.4б. Таким образом, при частотной модуляции реальным многочастотным сигналом, полоса модулированного сигнала (Пчм) оказывается значительно уже, по сравнению с полосой сигнала при фазовой модуляцией (Пфм). По этой причине, для целей радиосвязи и радиовещания предпочтение отдаётся частотной модуляции. 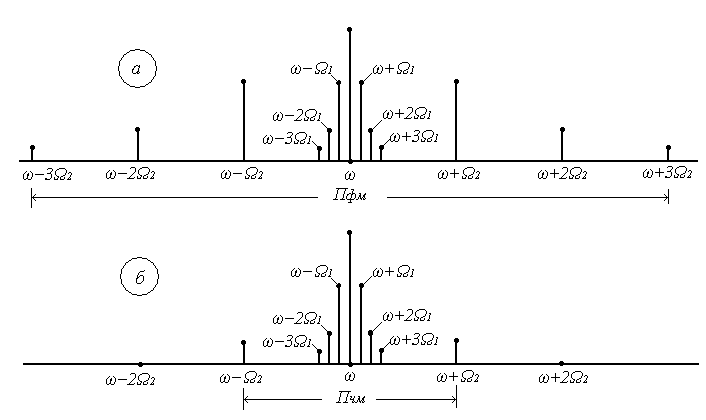 Рисунок 8.4 – Спектры сигналов с ФМ и ЧМ 8.3 Методы получения частотной модуляции Колебания с частотной модуляцией можно получить, либо непосредственно, изменяя частоту колебаний автогенератора, либо путём преобразования фазовой модуляции в частотную. Метод непосредственного изменения частоты получил название «прямого» метода ЧМ, соответственно преобразование ФМ в ЧМ называют «косвенным» методом. Прямые методы ЧМ основаны на изменении реактивности колебательной системы автогенератора под воздействием модулирующего сигнала. При косвенных методах фазовую модуляцию получают при прохождении несущего колебания через цепь, сдвиг фазы в которой зависит от модулирующего сигнала. Преобразование ФМ в ЧМ обеспечивается коррекцией модулирующего сигнала интегрирующей RC– цепью (см. п.п. 8.1). 8.3.1 Прямые методы ЧМ Для изменения частоты автогенератора в его колебательную систему включается управляемая реактивность. В качестве такой реактивности в настоящее время, как правило, используются ёмкость запертого p-n перехода специального полупроводникового диода – варикапа. В первом приближении ёмкость перехода может быть описана следующим выражением  (8.15)Здесь е -запирающее напряжение на варикапе; Со – ёмкость варикапа при е = 0; φк = 0,3 ÷ 0,5 В - контактная разность потенциалов; n- показатель «резкости» перехода, который может принимать значения от 0,3 до 3. Значение n = 0,3 соответствует «плавному» переходу; n = 0,5 – «резкому»; n ≥ 1 – «сверх резкому» переходу. Графики, соответствующие (9.15) приведены на рисунке 8.5б. Схема автогенератора с частотной модуляцией (без цепей питания) представлена на рисунке 8.5а 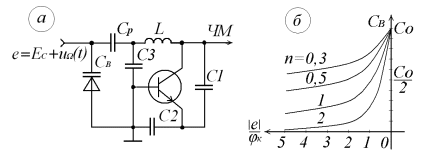 Рисунок 8.5 - Схема ЧМ автогенератора с варикапом Обычно ёмкости схемы автогенератора подбираются так, чтобы С3<<C1,C2 и СВ>C3. При этих условиях ёмкость контура в основном определяется ёмкостью варикапа Ск ≈ СВ . Резонансную частоту контура в этом случае можно определить следующим выражением  (8.16)Совершенно очевидно, что пропорциональная зависимость между резонансной частотой контура ωο и напряжением на переходе е (а значит и частотой генерируемых колебаний ω) возможна только при n = 2. В процессе модуляции е= Ес+иΩ(t)+ u(t)= Ес+UΩcosΩt + Ucosωt (8.17) Здесь Ес – напряжение смещения на варикапе; иΩ(t)- модулирующий сигнал; u(t)- колебания высокой частоты, поступающие на варикап со стороны автогенератора. Поскольку переход должен быть в закрытом состоянии (e<0), необходимо выполнить условие UΩ+ U≤ |Ec| (8.18) Полагая в (8.16) n=2, с учётом (8.17),для частоты генерируемых колебаний получим 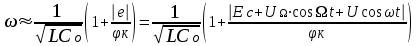 (8.19)Таким образом, для линейной частотной модуляции желательно иметь варикап со сверх резким переходом. На практике промышленные образцы варикапов обычно имеют резкие переходы с n ≈0,5. Поэтому приходится ограничивать величину девиации частоты. Для получения необходимой девиации, первичную модуляцию осуществляют на пониженной частоте, а затем с помощью умножителя переносят ЧМ колебание на рабочую частоту. При этом девиация частоты увеличивается в соответствии с кратностью умножения. Меньшие искажения при большей девиации могут быть получены с помощью «реактивного транзистора» (реактивной лампы) [12]. Реактивный транзистор представляет собой, как и варикап, управляемую реактивность (Хр)ёмкостного или индуктивного характера, подключаемую к контуру автогенератора. Схема реактивного транзистора представлена на рисунке 8.6а.  Рисунок 8.6 – Реактивный транзистор Для того, чтобы выходное сопротивление транзистора было реактивным, необходимо обеспечить фазовый сдвиг 900 между током коллектора  и коллекторным напряжением  . Поскольку коллекторный ток по фазе совпадает с базовым напряжением, соответствующий фазовый сдвиг должен быть между и 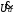 . В схеме реактивного транзистора необходимые фазовые сдвиги обеспечиваются с помощью простейшего фазовращателя (Z1,Z2), варианты которого представлены на рисунке 8.6б. Для того, чтобы такой фазовращатель обеспечивал фазовый сдвиг 900, необходимо выполнить условие |Z1|>>|Z2|. Тогда для напряжения на базе получим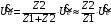 (8.20)При работе транзистора с отсечкой коллекторного тока 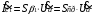 , поэтому с учётом (8.20), получим (8.21)В зависимости от вида использованного фазовращателя (рисунок 8.6б), выходное сопротивление реактивного транзистора можно представить следующим образом 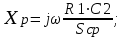 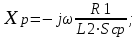  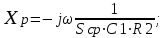 На основании полученных результатов можно сделать вывод, что реактивный транзистор имеет индуктивную реакцию, если Z1- индуктивность, или Z2- ёмкость. Ёмкостная реакция реактивного транзистора имеет место, если Z2- индуктивность, или Z1- ёмкость. Частотная модуляция в автогенераторе может быть получена путём изменения средней крутизны реактивного транзистора при работе с отсечкой коллекторного тока, т.к. в этом случае угол отсечки зависит от смещения на базе, т.е. от модулирующего напряжения е=Ес+uΩ(t). Основное достоинство прямых методов ЧМ заключается в возможности непосредственного получения больших отклонений частоты. Однако такая возможность приводит к существенной нестабильности средней частоты, которая будет меняться из-за нелинейности характеристики управляющего реактивного элемента (УЭ), а также вследствие нестабильности, или пульсаций, напряжения источников питания и влияния других внешних дестабилизирующих факторов (см. раздел 5.4). Использование ЧМ в кварцевых автогенераторах позволяет отчасти решить эту проблему [12]. Тем не менее, из-за высокой фиксирующей способности кварцевого автогенератора, получить требуемые значения девиации частоты удается далеко не всегда. Проблема стабильности средней частоты решается в схеме, представленной на рисунке 8.7. В этой схеме средняя частота автогенератора (ГПД), с помощью фазовой автоподстройки частоты, приводится к высокостабильной частоте опорного генератора (ОГ). 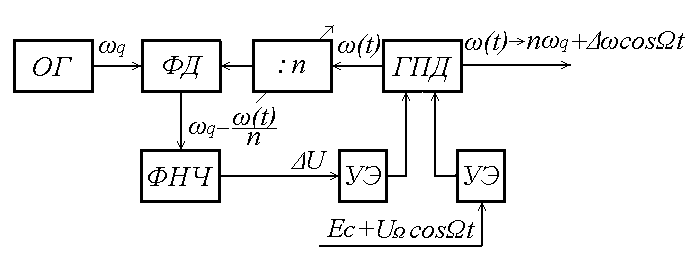 Рисунок 8.7 – Схема автоматической подстройки частоты. Делитель частоты в n раз необходим для уменьшения индекса модуляции. Выше было отмечено, что при некоторых значениях индекса модуляции (Ψ) несущая в спектре ЧМ исчезает, В этом случае велика вероятность сбоя в работе автоподстройки и соответственно вероятность скачкообразного изменения частоты ГПД. Чтобы исключить подобную ситуацию, индекс модуляции на входе фазового детектора (ФД) необходимо уменьшить до значения менее первого нуля функции Бесселя Jo (Ψ=2,4). Для надёжной работы системы фазовой автоподстройки (ФАП), уровень несущей должен быть достаточно большим, поэтому n подбирается так, чтобы индекс модуляции на входе ФД не превышал 1. Чтобы система ФАП не подавляла частотную модуляцию, она не должна действовать на частотах модулирующего сигнала. С этой целью, полоса пропускания фильтра нижних частот (ФНЧ) ограничивается частотой 5 ÷ 10 Гц. Поскольку частота звуковых сигналов обычно лежит выше 30 Гц, цепь обратной связи на этих частотах обрывается. Таким образом, ФАП реагирует только на медленные изменения частоты ГПД, обусловленные нестабильностью его средней частоты. Средняя частота на выходе ГПД составит nωq , и её стабильность будет соответствовать стабильности частоты опорного генератора. В качестве управляющих элементов (УЭ) в схеме обычно используются варикапы. Т.к. управляющее напряжение ФАП (ΔU) смещает рабочую точку на характеристике УЭ, во избежание нелинейных искажений, для ЧМ рекомендуется использовать отдельный УЭ. 8.3.2 Косвенные методы частотной модуляции В отличие от прямых методов ЧМ, преобразование фазовой модуляции в частотную исключает воздействие УЭ на несущую (среднюю) частоту модулированных колебаний. Поэтому необходимая стабильность средней частоты при косвенных видах ЧМ обеспечивается достаточно просто. Для осуществления ЧМ косвенным методом необходим фазовый модулятор. Простейший способ получения фазовой модуляции с преобразованием в ЧМ представлен на рисунке 8.8а 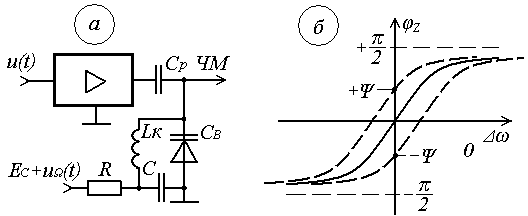 Рисунок 8.8 – Схема ЧМ с фазовым модулятором Здесь R,C – интегрирующая цепь; Ср – разделительная ёмкость. Конденсатор С выполняет также функции блокировочной ёмкости в контуре Lк, СВ. Фазовая характеристика параллельного контура имеет вид φz(ω) = arctg[2(ω- ω0)Q/ω0]= arctg(2ΔωQ/ω0). С учётом (5.14), φz(ω)= - arctg(ΔСВ∙Q/СВ) (8.22) Из последнего выражения следует, что даже при линейной зависимости ΔСВ от модулирующего сигнала, линейная фазовая модуляция возможна лишь при небольших расстройках контура относительно рабочей частоты генератора. Практически, линейный участок фазовая характеристика контура (рисунок 8.8б) имеет лишь при индексе модуляции Ψ ≤ 0,5. В [14] описана трёхконтурная схема фазового модулятора, которая при нелинейных искажениях менее 2% позволила получить индекс модуляции порядка 2 радиан. Схема частотной модуляции с трёхконтурным фазовым модулятором представлена на рисунке 8.9 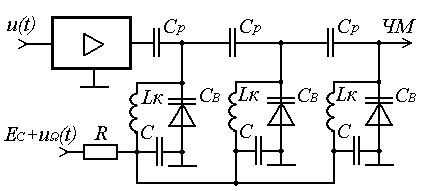 Рисунок 8.9 – Схема частотной модуляции с 3-х контурным фазовым модулятором В этой схеме ёмкость интегрирующей цепи определяется суммой ёмкостей трёх конденсаторов С. Основной недостаток рассмотренных схем – паразитная амплитудная модуляция, которая появляется вследствие изменения эквивалентного сопротивления контура при его расстройке. На рисунке 8.10 представлена мостовая схема фазового модулятора свободная от этого недостатка [15].  Рисунок 8.10 – Схема ЧМ с мостовым фазовым модулятором В этой схеме инверсный усилитель с разделённой нагрузкой обеспечивает два противофазных и равных по величине напряжения u1 и u2. Электрический мост образуют два нагрузочных резистора, резистор R1 и реактивная цепь, состоящая из ёмкости варикапа СВ и индуктивности L. Принцип работы фазового модулятора иллюстрируется векторной диаграммой на рисунке 8.10. К одной диагонали моста приложена сумма напряжений u1 + u2, а выходное напряжение и снимается с другой диагонали. Поскольку напряжения на реактивной цепи (uС + uL) и на резисторе R1(uR) всегда сдвинуты по фазе на 900, вектор выходного напряжения (и) изменяет своё положение в зависимости от величины сопротивления реактивной цепи, оставаясь постоянным по величине. Сопротивление реактивной цепи (Х) модулируется информационным сигналом (иΩ) с помощью ёмкости варикапа 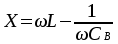 . Такой модулятор позволяет получить индекс модуляции порядка одного радиана при допустимых нелинейных искажениях без паразитной амплитудной модуляции.В радиопередатчиках УКВ-ЧМ вещания, производства 60-х – 70-х годов, для частотной модуляции использовалась схема фазового модулятора, структурная схема которого представлена на рисунке 8.11.  Рисунок 8.11 – Схема ЧМ с импульсно-фазовым модулятором На рисунке приняты следующие обозначения: ОГ – опорный генератор; ГПН – генератор пилообразного напряжения; ШИМ – широтно-импульсный модулятор; ГКИ –генератор коротких импульсов; 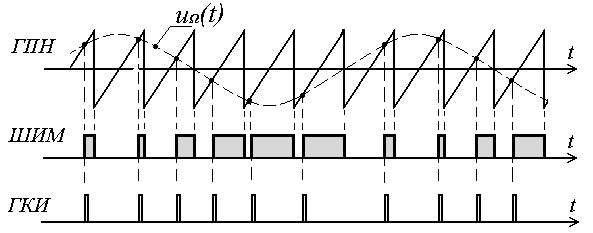 – умножитель частоты. Диаграммы напряжений в некоторых точках схемы представлены на рисунке 8.12. Рисунок 8.12 – Диаграмма напряжений в фазовом модуляторе Первый график на диаграмме иллюстрирует форму напряжения на выходе ГПН; здесь же показано модулирующее напряжение uΩ(t) на входе ШИМ, в качестве которого используется компаратор. В результате сравнения пилообразного и модулирующего напряжений на выходе ШИМ, получается импульсный сигнал, модулированный по длительности. ГКИ генерирует импульсы, положение которых синхронизировано с задними фронтами импульсов с ШИМ. В результате на входе умножителя частоты формируется сигнал с фазо-импульсной модуляцией. В качестве умножителя частоты может быть использован генератор с внешним возбуждением, контур которого настраивается на n-ю гармонику импульсной последовательности ГКИ. Таким образом, на выходе устройства получаем гармонический сигнал с фазовой модуляцией. Поскольку модулирующий сигнал проходит на вход ШИМ через интегрирующую RC цепь, ФМ преобразуется в ЧМ. Если бы пилообразное напряжение ГПН имело идеальную форму с вертикальным передним фронтом, положение импульсов ГКИ можно было бы менять в пределах всего периода средней (несущей) частоты. При этом индекс модуляции составил бы 3,14 радиана. Реально же, вследствие конечной длительности фронта, удаётся получить индекс порядка 2,6 радиан. С помощью умножителя индекс частотной модуляции увеличивается соответственно в nраз. Благодаря линейному нарастанию пилообразного напряжения такое устройство обеспечивает высокое качество частотной модуляции (минимальные нелинейные искажения). Определим необходимую кратность умножения частоты при использовании такого модулятора для УКВ-ЧМ радиовещания. Согласно ГОСТ девиация частоты на выходе передатчика должна составлять 50 кГц [16]. Это означает, что на нижней звуковой частоте 30 Гц индекс ЧМ составит 1667 радиан, а необходимая кратность умножения частоты n=1667/2,6=641 раз. При такой кратности умножения и большой величине индекса модуляции, спектры соседних гармоник, также модулированных по частоте, начинают перекрываться. Отделить помеху основному сигналу становится невозможно, и она воспринимается как повышенный уровень шумов. По мере ужесточения требований к допустимому уровню шумов от косвенных методов ЧМ в радиовещании пришлось отказаться. В современных разработках радиовещательных передатчиков исключительное применение находят прямые методы частотной модуляции с автоподстройкой средней частоты по опорному генератору. Контрольные вопросы В чём заключается отличие частотной модуляции от фазовой? Что такое «прямой» и «косвенный» методы формирования сигнала с частотной модуляцией? Что такое девиация частоты и индекс угловой модуляции? Почему в радиовещательных передатчиках используется частотная, а не фазовая модуляция? Каким образом решается проблема стабилизации средней частоты при прямых методах частотной модуляции? Дайте сравнительную оценку прямых и косвенных методов частотной модуляции. |