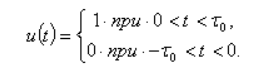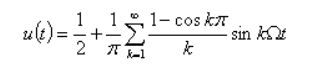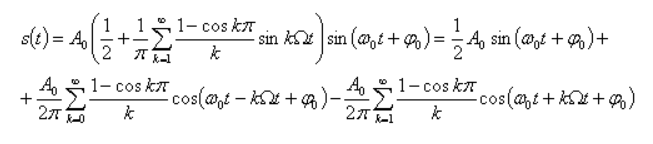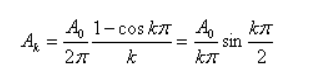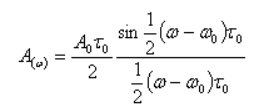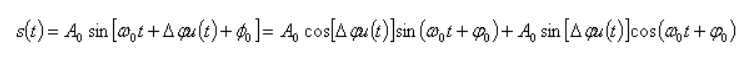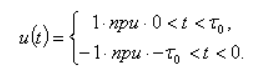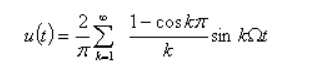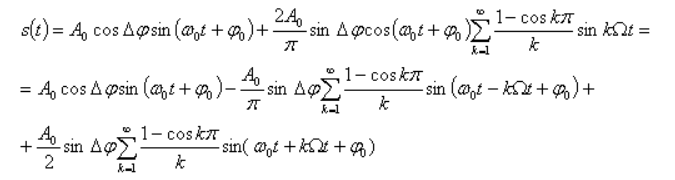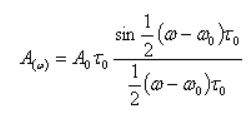|
|
Модуляция при передачи дискретных сигналов. МигельКА_КТбо2-4_реферат1. Модуляция при передачи дискретных сигналов по дисциплине Компьютерные сети
МИНОБРНАУКИ РОССИИ
Федеральное государственное автономное образовательное учреждение
высшего образования
«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Инженерно-технологическая академия
Институт компьютерных технологий и информационной безопасности
Кафедра систем автоматизированного проектирования
Реферат
на тему: «Модуляция при передачи дискретных сигналов»
по дисциплине «Компьютерные сети»
Выполнил студент гр. КТбо2-4
Мигель К.А._________________
Проверил профессор каф. САПР
Нужнов Е.В.__________________
Таганрог
2020
СОДЕРЖАНИЕ
ВВЕДЕНИе
Модуляция – это процесс преобразования данных в электрические сигналы, оптимизированный для передачи. Методы модуляции условно подразделяются на четыре типа: аналоговая модуляция, цифровая модуляция, импульсная модуляция и метод с расширенным спектром.
Аналоговая модуляция обычно используется для AM, FM-радио и коротковолнового вещания.
Цифровая модуляция включает передачу двоичных сигналов (0 и 1).
Этот метод разделен на модуляцию с одной несущей, посредством которой несущая занимает всю ширину полосы (т.е. амплитуду, частоту и фазу), и схему с несколькими несущими, которая модулирует и передает разные данные на нескольких несущих.
Кроме того, существует метод импульсной модуляции, используемый для изменения ширины импульса и метода расширенного спектра, который распространяет энергию сигнала по широкой полосе.
Модуляция при передаче дискретных сигналов
При передаче дискретной информации посредством модуляции единицы и нули кодируются изменением амплитуды, частоты или фазы несущего синусоидального сигнала. В случае, когда модулированные сигналы передают дискретную информацию, вместо термина «модуляция» иногда используется термин «манипуляция»: амплитудная манипуляция (Amplitude Shift Keying, ASK), частотная манипуляция (Frequency Shift Keying, FSK), фазовая манипуляция (Phase Shift Keying, PSK).
Пожалуй, самый известный пример применения модуляции при передаче дискретной информации — это передача компьютерных данных по телефонным каналам. Типичная амплитудно-частотная характеристика стандартного абонентского канала, называемого также каналом тональной частоты, представлена на Рисунке 1. Этот составной канал проходит через коммутаторы телефонной сети и соединяет телефоны абонентов. Канал тональной частоты передает частоты в диапазоне от 300 до 3400 Гц, таким образом, его полоса пропускания равна 3100 Гц. Такая узкая полоса пропускания вполне достаточна для качественной передачи голоса, однако она недостаточно широка для передачи компьютерных данных в виде прямоугольных импульсов. Решение проблемы было найдено благодаря аналоговой модуляции. Устройство, которое выполняет функцию модуляции несущей синусоиды на передающей стороне и обратную функцию демодуляции на приемной стороне, носит название модема (модулятор-демодулятор).
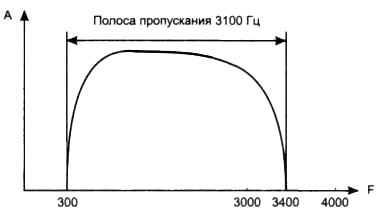
Рисунок 1
На Рисунке 2 показаны различные типы модуляции, применяемые при передаче дискретной информации. Исходная последовательность битов передаваемой информации приведена на диаграмме, представленной на Рисунке. 2, а.
При амплитудной модуляции для логической единицы выбирается один уровень амплитуды синусоиды несущей частоты, а для логического нуля — другой (Рисунке 2, б). Этот способ редко используется в чистом виде на практике из-за низкой помехоустойчивости, но часто применяется в сочетании с другим видом модуляции — фазовой модуляцией.
При частотной модуляции значения нуля и единицы исходных данных передаются синусоидами с различной частотой — f0 и f1 (Рисунке 2, в). Этот способ модуляции не требует сложных схем и обычно применяется в низкоскоростных модемах, работающих на скоростях 300 и 1200 бит/с. При использовании только двух частот за один такт передается один бит информации, поэтому такой способ называется двоичной частотной манипуляцией (Binary FSK, BFSK). Могут также использоваться четыре различные частоты для кодирования двух битов информации в одном такте, такой способ носит название четырехуровневой частотной манипуляции (four-level FSK). Применяется также название многоуровневая частотная манипуляция (Multilevel FSK, MFSK).
При фазовой модуляции значениям данных 0 и 1 соответствуют сигналы одинаковой частоты, но различной фазы, например 0 и 180° или 0,90,180 и 270° (Рисунке 2, г). В первом случае такая модуляция носит название двоичной фазовой манипуляции (Binary PSK, BPSK), а во втором — квадратурной фазовой манипуляции (Quadrature PSK, QPSK)[1].
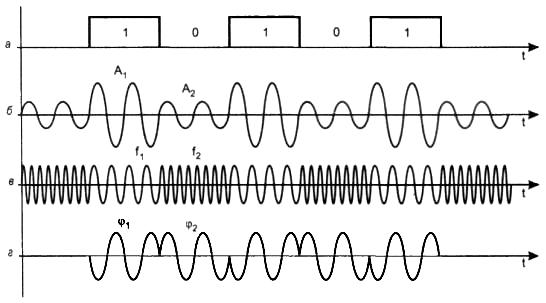
Рисунок 2
2. Сигналы при дискретной модуляции
При дискретной модуляции закодированное сообщение u(t), представляющее собой последовательность кодовых символов {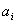 }, преобразовывается в последовательность элементов сигнала { }, преобразовывается в последовательность элементов сигнала {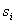 }. Последние отличаются от кодовых символов лишь электрическим представлением. В частном случае дискретная модуляция состоит в воздействии кодовых символов {аi} на переносчик f(t). Такая дискретная модуляция аналогична непрерывной. }. Последние отличаются от кодовых символов лишь электрическим представлением. В частном случае дискретная модуляция состоит в воздействии кодовых символов {аi} на переносчик f(t). Такая дискретная модуляция аналогична непрерывной.
Посредством модуляции один из параметров переносчика изменяется по закону, определяемому кодом. При непосредственной передаче переносчиком может быть постоянный ток, изменяющимися параметрами которого являются величина и направление. Обычно же в качестве переносчика, как и при непрерывной модуляции, используется переменный ток (гармоническое колебание). В этом случае можно получить амплитудную (AM), частотную (ЧМ) и фазовую (ФМ) модуляции. Дискретную модуляцию часто называют манипуляцией, а устройство, осуществляющее дискретную модуляцию (дискретный модулятор), называют манипулятором или генератором сигналов.
На Рисунке 3 приведены графики сигналов при различных видах манипуляции. При AM символу 1 соответствует передача несущего колебания в течение времени 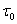 (посылка), символу 0 — отсутствие колебания (пауза). При ЧМ передача несущего колебания с частотой (посылка), символу 0 — отсутствие колебания (пауза). При ЧМ передача несущего колебания с частотой 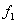 соответствует символу 1, а передача колебания соответствует символу 1, а передача колебания 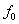 соответствует 0. При ФМ меняется фаза несущей на 180° при каждом переходе от 1 к 0 и от 0 к 1. соответствует 0. При ФМ меняется фаза несущей на 180° при каждом переходе от 1 к 0 и от 0 к 1.
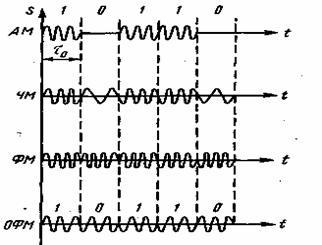
Рисунок 3
Наконец, в настоящее время применяется относительная фазовая модуляция (ОФМ). В отличие от ФМ, в системе ОФМ фаза несущего колебания изменяется на 180° при передаче символов 1 и остается неизменной при передаче символов 0.
При ОФМ манипуляция каждой данной посылки осуществляется относительно предыдущей. Очевидно, таким способом можно манипулировать (изменять) любой параметр несущего колебания: при изменении частоты получим относительную частотную манипуляцию (ОЧМ), при изменении амплитуды относительную амплитудную манипуляцию (ОАМ). Дельта-модуляция, также является одним из видов относительной манипуляции.
Рассмотрим спектры сигналов при некоторых видах дискретной модуляции. Будем полагать, что модуляция производится двоичным сообщением u(t), представляющим собой периодическую последовательность прямоугольных импульсов с периодом 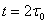 . .
Амплитудная манипуляция. Сигнал AM можно записать в виде
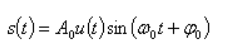
где периодическая функция u(t) на интервале 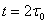 равна: равна:
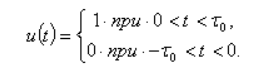
Представим u(t) рядом Фурье
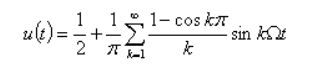
Тогда сигнал AM запишется в виде
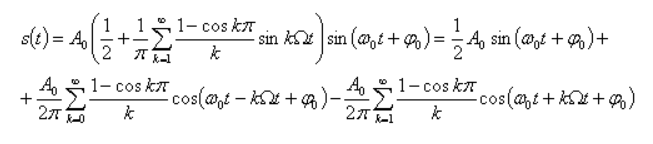
Спектр сигнала AM показан на Рисунке 4. Он состоит из несущего колебания с амплитудой 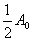 и двух боковых полос, спектральные составляющие которых имеют амплитуды и двух боковых полос, спектральные составляющие которых имеют амплитуды
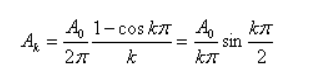
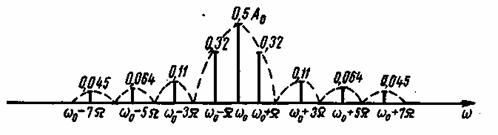
Рисунок 4
Огибающая спектра дискретного сигнала AM выражается формулой
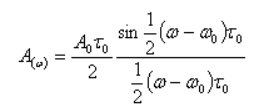
т. е. представляет собой смещенный на частоту 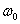 спектр одиночного импульсного сигнала u(t). спектр одиночного импульсного сигнала u(t).
Фазовая манипуляция. Сигнал ФМ можно записать в виде
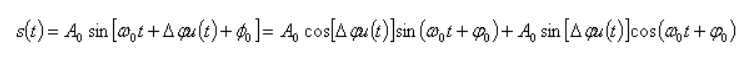
Периодическая функция, определяющая закон изменения фазы на интервале 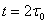 , выражается формулой , выражается формулой
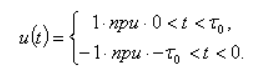
Подставив формула получим:
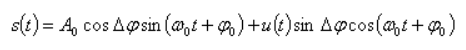
Представим u(t) рядом Фурье
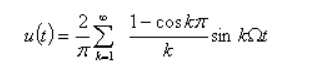
Тогда сигнал ФМ запишется в виде
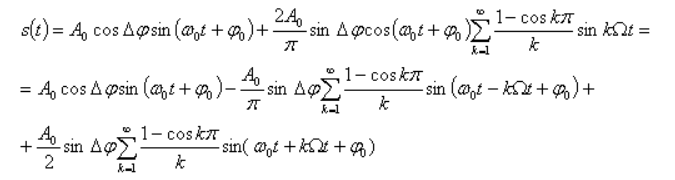
Спектр сигнала ФМ для различных значений девиаций фазы показан на Рисунке 5. Он состоит из несущего колебания и двух боковых полос. Амплитуда несущего колебания зависит от 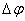 : : 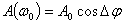 и при и при 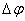 = =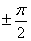 — обращается в 0. Амплитуды спектральных составляющих в боковых полосах также зависят от — обращается в 0. Амплитуды спектральных составляющих в боковых полосах также зависят от 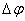 . При увеличении . При увеличении  от 0 до от 0 до 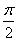 , как видно из Рисунка 5, амплитуда несущего колебания убывает до нуля, а амплитуды боковых частот увеличиваются. , как видно из Рисунка 5, амплитуда несущего колебания убывает до нуля, а амплитуды боковых частот увеличиваются.
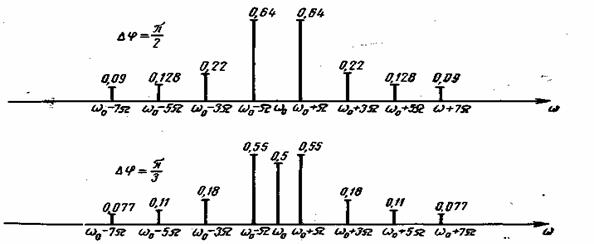
Рисунок 5
Когда  = =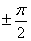 — вся энергия сигнала ФМ содержится только в боковых полосах. Так же, как и при AM, огибающая дискретного спектра боковых частот представляет собой смещенный на частоту — вся энергия сигнала ФМ содержится только в боковых полосах. Так же, как и при AM, огибающая дискретного спектра боковых частот представляет собой смещенный на частоту 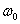 спектр одиночного импульсного сигнала u(t), умноженный нa sin спектр одиночного импульсного сигнала u(t), умноженный нa sin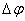 : :
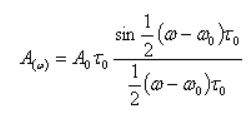
Аналогично определяется спектр сигнала при частотной манипуляция[2].
3. Цифровая фазовая модуляция
Наиболее простой тип PSK называется двоичной фазовой манипуляцией (BPSK, binary phase shift keying), где «двоичный» относится к использованию двух фазовых смещений (одно для логической единицы и одно для логического нуля).
Мы интуитивно можем признать, что система будет более надежной, если разделение между этими двумя фазами будет большим – конечно, приемнику будет сложно различать символ со смещением фазы 90° от символа со смещением фазы 91°. Для работы у нас есть диапазон фаз 360°, поэтому максимальная разница между фазами логической единицы и логического нуля составляет 180°. Но мы знаем, что переключение синусоиды на 180° – это то же самое, что ее инвертирование; таким образом, мы можем думать о BPSK как о простом инвертировании сигнала несущей в ответ на одно логическое состояние и оставление ее в исходном состоянии в ответ на другое логическое состояние.
Чтобы сделать следующий шаг, мы вспомним, что умножение синусоиды на отрицательную единицу – это то же самое, что ее инвертирование. Это приводит к возможности внедрения BPSK с использованием следующей базовой аппаратной конфигурации:
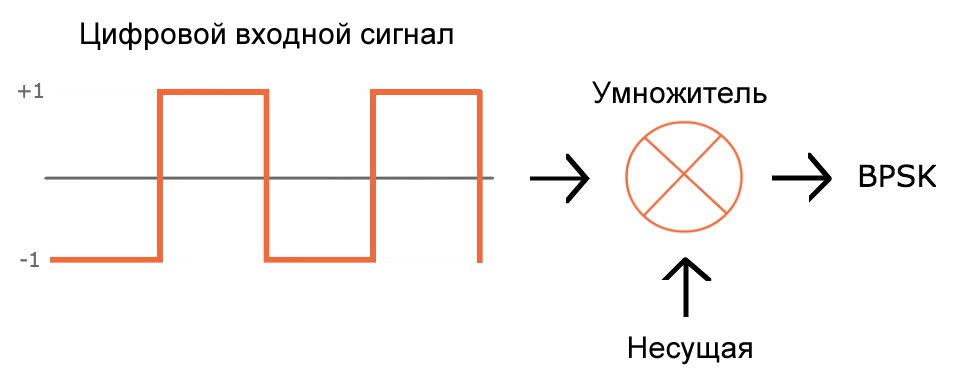
Рисунок 6 - Базовая схема получения BPSK сигнала
Однако эта схема легко может привести к переходам с высоким наклоном в форме сигнала несущей частоты: если переход между логическими состояниями происходит, когда сигнал несущей находится в своем максимальном значении, напряжение сигнала несущей должно быстро перейти к минимальному значению.
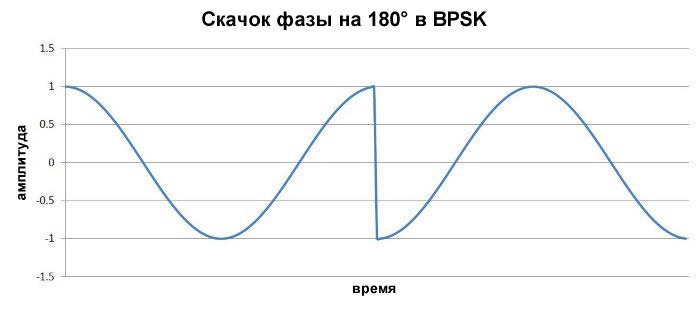
Рисунок 7 - Высокий наклон в форме BPSK сигнала при изменении логического состояния модулирующего сигнала
Такие события с высоким наклоном нежелательны, потому что они создают энергию на высокочастотных составляющих, которые могут помешать другим радиочастотным сигналам. Кроме того, усилители имеют ограниченную способность производить резкие изменения в выходном напряжении.
Если мы усовершенствуем вышеприведенную реализацию двумя дополнительными функциями, то сможем обеспечить плавные переходы между символами. Во-первых, нам необходимо убедиться, что период цифрового бита равен одному или нескольким полным периодам сигнала несущей. Во-вторых, нам необходимо синхронизировать цифровые переходы с сигналом несущей. Благодаря этим усовершенствованиям мы могли бы разработать систему таким образом, чтобы изменение фазы на 180° происходило, когда сигнал несущей частоты находится в пересечении нуля (или близко к нему).
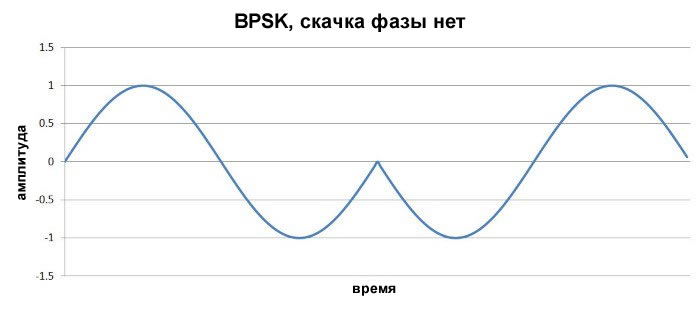
Рисунок 8 - BPSK сигнал; нет резкого скачка напряжения сигнала несущей при изменении логического состояния модулирующего сигнала
BPSK передает один бит на символ, к чему мы и привыкли. Всё, что мы обсуждали в отношении цифровой модуляции, предполагало, что сигнал несущей изменяется в зависимости от того, находится ли цифровое напряжение на низком или высоком логическом уровне, и приемник воссоздает цифровые данные, интерпретируя каждый символ как 0 или 1.
Прежде чем обсуждать квадратурную фазовую манипуляцию (QPSK, quadrature phase shift keying), нам необходимо ввести следующую важную концепцию: нет причин, по которым один символ может передавать только один бит. Это правда, что мир цифровой электроники строится вокруг схем, в которых напряжение находится на одном или другом экстремальном уровне, так что напряжение всегда представляет собой один цифровой бит. Но радиосигнал не является цифровым; скорее, мы используем аналоговые сигналы для передачи цифровых данных, и вполне приемлемо разработать систему, в которой аналоговые сигналы кодируются и интерпретируются таким образом, чтобы один символ представлял два (или более) бита[5].
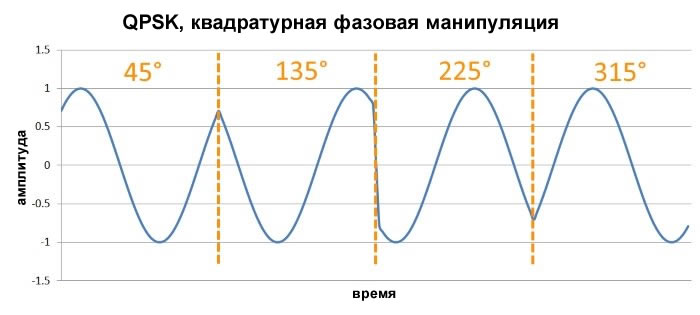
Рисунок 9 - QPSK сигнал во временной области
Преимущество QPSK заключается в более высокой скорости передачи данных: если мы сохраняем одну и ту же длительность символа, то можем удвоить скорость передачи данных от передатчика к приемнику. Недостатком является сложность системы. (Вы можете подумать, что QPSK более восприимчив к битовым ошибкам, чем BPSK, поскольку разделение между возможными значениями в нем меньше. Это разумное предположение, но если вы рассмотрите их математику, то оказывается, что вероятности ошибок на самом деле очень похожи.)
Дифференциальное кодирование
Еще одна сложность заключается в том, что демодуляция PSK сигналов сложнее, чем FSK сигналов. Частота является «абсолютной» в том смысле, что изменения частоты всегда можно интерпретировать, анализируя изменения сигнала во времени. Фаза, однако, относительна в том смысле, что она не имеет универсальной опорной точки – передатчик генерирует изменения фазы относительно одного момента времени, а приемник может интерпретировать изменения фазы относительно другого момента времени.
Практическое проявление этого заключается в следующем: если между фазами (или частотами) генераторов, используемых для модуляции и демодуляции, существуют различия, PSK становится ненадежной. И мы должны предположить, что будут разности фаз (если приемник не включает в себя схему восстановления несущей).
Дифференциальная QPSK (DQPSK, differential QPSK) – это вариант, который совместим с некогерентными приемниками (т.е. приемниками, которые не синхронизируют генератор демодуляции с генератором модуляции). Дифференциальная QPSK кодирует данные, создавая определенный сдвиг фазы относительно предыдущего символа таким образом, чтобы схема демодуляции анализировала фазу символа, используя опорную точку, которая является общей и для приемника, и для передатчика[3].
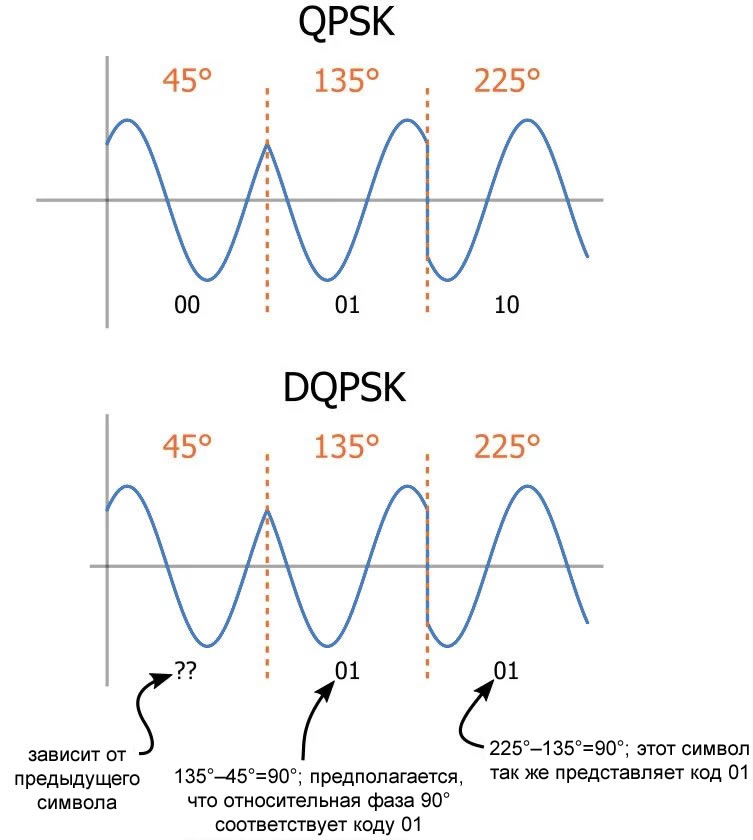
Рисунок 10 - Пояснение принципа действия DQPSK модуляции
4. Мультиплексирование с ортогональным частотным разделением (OFDM)
Несмотря на то, что метод дословно расшифровывается как мультиплексирование с ортогональным частотным разделением, его все-таки в первую очередь относят к методам цифровой модуляции. Дело в том, что метод OFDM использует одновременно и модуляцию и мультиплексирование, но мультиплексирование особенное. Обычное мультиплексирование подразумевает объединение различных сигналов от разных источников, здесь же происходит объединение составных частей одного и того же сигнала.
Постараемся объяснить все на простом примере. Представьте, что нам надо передать из одного пункта в другой стеклянный витраж. Для этого в нашем распоряжении есть некоторый ресурс, допустим 4 тележки (в случае передачи информации в качестве ресурса можно было бы считать доступный для передачи диапазон частот).
В случае OFDM мы разбираем наш стеклянный витраж на некоторое определенное количество частей, для примера пусть их будет 4. Далее каждая тележка перевозит свою часть посылки (витража), при этом тележки катятся одновременно параллельно друг другу. Допустим на пути у нас встречается одна преграда в виде камня (в случае передачи информации – узкополосная помеха). Одна из тележек наезжает на камень, соответственно одна из частей посылки не доходит до пункта приема.
Однако большее количество частей витража все-таки было корректно получено, поэтому с помощью интуиции и волшебства (помехоустойчивого кодирования), есть шанс восстановить недостающую в результате падения одной тележки часть посылки.
Как бы все было, не применяя OFDM? При традиционном подходе для наискорейшей передачи всей посылки мы также задействуем все доступные ресурсы, но будем транспортировать витраж целиком на всех 4 тележках (используем высокоскоростной метод модуляции, занимающий всю полосу канала). Допустим, на пути у нас также встречается одна преграда в виде камня. В результате одна из тележек наезжает на камень, витраж падает и разбивается вдребезги.
Алгоритма, по которому в данном случае распался на части наш витраж, мы не знаем, поэтому собрать по кусочкам заново мы его не можем. Итог: целый витраж не доехал до пункта приема (потерян немалый объем данных, здесь даже помехоустойчивое кодирование нас не спасет).
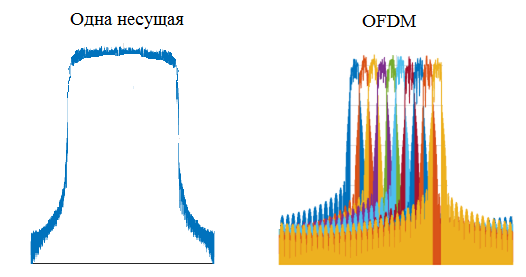
Рисунок 11
Одной из особенностью OFDM является то, что все тележки могут двигаться параллельно практически вплотную и при этом не мешать друг другу. При передаче информации роль тележек выполняют поднесущие сигналы, т.е. множество несущих колебаний (если забыли, что это такое, почитайте в любом учебнике основы модуляции). Вспомним фильм Терминатор 2 и представим, что тележки сделаны из жидкого металла. В связи с этим даже если при движении пути тележек частично перекрываются, они не мешают друг другу, комфортно сосуществуют вместе и движутся дальше. Существует аналогичный эффект по отношению к передаче сигналов – ортогональность сигналов. Обычно для объяснения термина ортогональность сигналов приводят интегральное математическое выражение. Однако поскольку было дано обещание объяснять все на пальцах, можно просто уяснить следующее. Ортогональные сигналы обладают замечательным свойством – их взаимная энергия равна нулю. Ортогональность поднесущих позволяет на приёме выделить каждую из них из общего сигнала даже в случае частичного перекрытия их спектров. Поскольку поднесущие располагаются вплотную друг к другу и даже частично накладываются друг на друга (Рисунок 12) спектральная эффективность модулированного OFDM сигнала получается высокой.
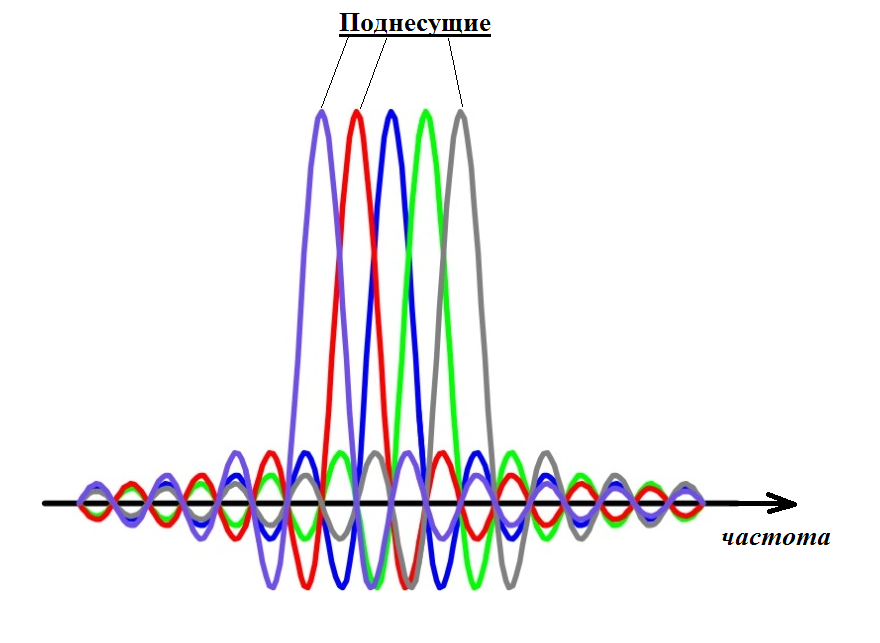
Рисунок 12
Как видно из рисунка, каждая поднесущая представлена отдельным пиком. Обратите внимание, что в точке пика каждой поднесущей значение остальных поднесущих равно нулю. На оси времени каждой кривой соответствует свой модулированный сигнал. Сумма всех этих сигналов дает сложный по форме OFDM-сигнал[4].
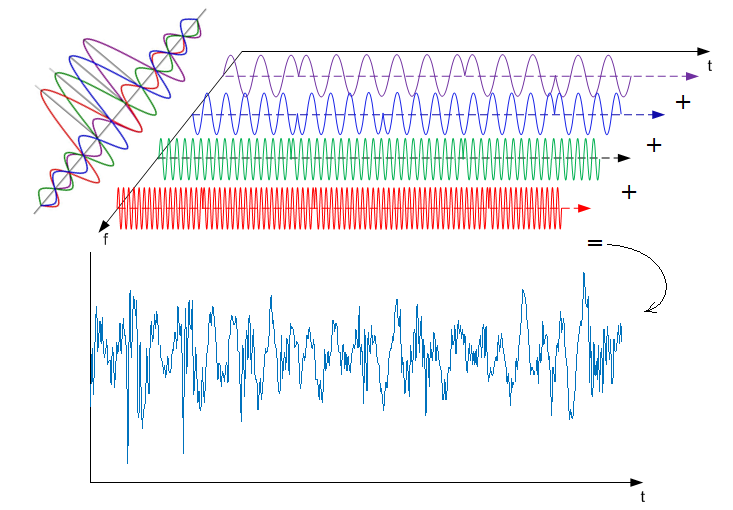
Рисунок 13
Параметры поднесущих сигналов (например, синусойд) подбираются таким образом, чтобы они были по отношению друг к другу ортогональны. Для быстрой реализации данного действия с помощью вычислительных устройств используют алгоритм обратного быстрого преобразования Фурье (ОБПФ). То есть мы нарочно представляем, что значения сигнала перед блоком ОБПФ относятся к частотной области. Тогда на выходе блока ОБПФ мы получаем значения сигнала на временной оси. Объединяя все значения, мы получаем сложный составной OFDM сигнал.
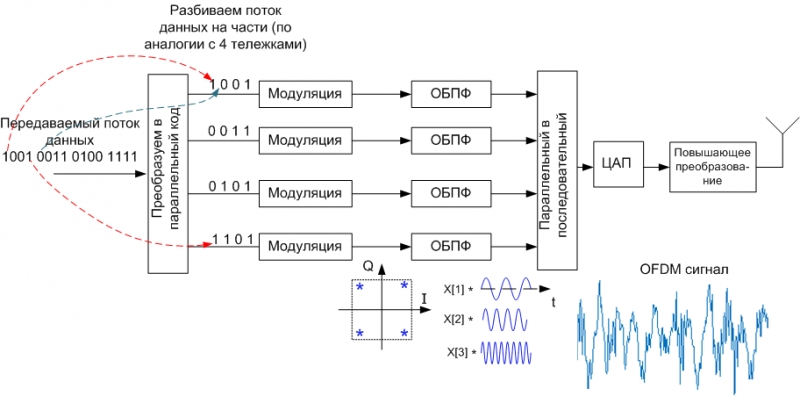
Рисунок 14
Важно отметить, что в данной упрощенной схеме представлены не все блоки, имеющиеся в реальных системах с OFDM. Здесь для упрощения схемы не приведены блоки добавления защитных бит и циклического префикса, являющегося неотъемлемой частью технологии.
В виду того, что ОБПФ работает эффективно с массивами размерности 2^k, количество поднесущих выбирается аналогичной кратности. Например, в WiMAX число поднесущих выбирается от 128 до 2048 и может занимать полосы частот от 1,25 МГц до 20 МГц.
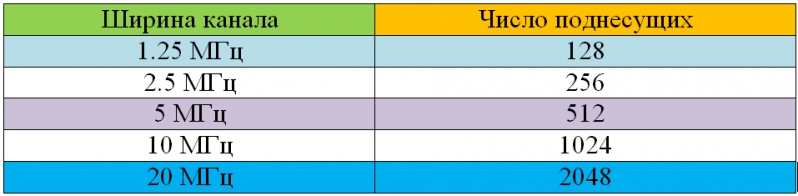
Рисунок 15
Для каждой из поднесущих используется свой формат модуляция в зависимости от требований и величины помех в канале[6].
ЗАКЛЮЧЕНИЕ
При разработке системы беспроводной связи всегда существует компромисс между эффективностью полосы пропускания и эффективностью энергопотребления, когда речь идет о выборе подходящей схемы модуляции. Появление VLSI и DSP позволило инженеру связи применять более экономичные и надежные методы цифровой модуляции для поддержки современных данных и мультимедийных приложений, таких как голос и видео. В отличие от аналоговой модуляции, цифровая модуляция позволяет разработчику использовать многие методы цифровой обработки сигналов, такие как прямое исправление ошибок, что позволяет осуществлять связь в жестких условиях канала.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Модуляция при передаче дискретных сигналов // URL: http://iptcp.net/modulyatsiya-pri-peredache-diskretnykh-signalov.html [Электронный ресурс] / [Режим доступа: свободный] / (Дата обращения: 12.06.2020).
Сигналы при дискретной модуляции // URL: https://siblec.ru/telekommunikatsii/teoriya-peredachi-signalov/3-modulirovannye-signaly [Электронный ресурс] / [Режим доступа: свободный] / (Дата обращения: 12.06.2020).
Цифровая фазовая модуляция: BPSK, QPSK, DQPSK // URL: https://radioprog.ru/post/404 [Электронный ресурс] / [Режим доступа: свободный] / (Дата обращения: 12.06.2020).
Просто о сложном: OFDM-модуляция// URL: https://nag.ru/articles/article/32365/prosto-o-slojnom-ofdm-modulyatsiya.html [Электронный ресурс] / [Режим доступа: свободный] / (Дата обращения: 12.06.2020).
Tony J. Rouphael. RF and Digital Signal Processing for Software-Defined Radio: A Multi-Standard Multi-Mode Approach. - Newnes is an imprint of Elsevier: Нью-Йорк, 2008.
Modulation Methods// URL: https://www.rohm.com/electronics-basics/wireless/modulation-methods#: :text=Modulation%20Method%20Classification,modulation%20%2C%20and%20Spread%20spectrum%20method. [Электронный ресурс] / [Режим доступа: свободный] / (Дата обращения: 12.06.2020).
|
|
|
 Скачать 0.94 Mb.
Скачать 0.94 Mb.