9.3A бөлім: Үшбұрыштарды шешу
|
Мектеп:
|
Күні:
|
Мұғалімнің аты-жөні:
|
Сынып: 9
|
Қатысқандар саны:
|
Қатыспағандар саны:
|
Сабақ тақырыбы
|
Қолданбалы есептерді шешу
|
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)
|
9.1.3.10 синустар және косинустар теоремаларын үшбұрыштарды шешуде және қолданбалы есептерді шығаруда қолдану
|
Сабақ мақсаттары
|
Үшбұрыштарды шешу теоремаларын ажырату;
Үшбұрыштарды шешу теоремаларын қолданбалы есептер шығаруда қолдану;
Үшбұрыштарды шешу теоремаларын өмірмен байланысқан күрделі есептерді шығаруда қолдану.
|
Бағалау критерийлері
|
Үшбұрыштарды шешу теоремаларын анықтайды;
Косинустар теоремасын, синустар теоремасын қолданбалы есептер шығаруда қолданады;
Үшбұрыштарды шешу теоремаларын қолданып өмірмен байланысты күрделі есептерді шешеді.
|
Тілдік мақсаттар
|
Оқушылар:
теоремалар мен формулаларды қолданып есептерді шешу жолын түсіндіреді;
Пәнге қатысты лексика мен терминология:
үшбұрыштарды шешу;
синустар теоремасы;
косинустар теоремасы.
Диалогқа/жазылымға қажетті тіркестер:
үшбұрыштың кез-келген қабырғасының квадраты ... ;
... қарсы жатқан бұрыштардың синустарына пропорционал.
|
Құндылықтарды дарыту
|
«Мәңгілік ел» құндылығы: Индустрияландыру мен инновацияларға негізделген экономикалық өсу
«Білім беру» құндылығы: Еңбек және шығармашылық, өмір бойы білім алуды қалыптастыру
|
Пәнаралық
байланыстар
|
Синустар мен косинустар теоремасының шығу тарихы туралы мәліметтер арқылы тарихпен, үшбұрыштарды шешудің геодезия мен навигацияда, астрономияда қолданылуы туралы айтып география, астрономия, физика пәндерімен байланыстыру
|
АКТ қолдану дағдылары
|
Инженерлік калькуляторды қолданады, қосымша дереккөздермен жұмыс және интербелсенді тақтадан білімдерін тексеріп отырады
|
Бастапқы білім
|
Үшбұрышқа іштей сызылған және сырттай сызылған шеңберлерді білу, үшбұрыштардың түрлерін, үшбұрыштың теңсіздігін, үшбұрыштың қабырғалары мен бұрыштарының арасындағы қатынасты, үшбұрыштың аудан формулаларын білу, тікбұрышты үшбұрыштарды шеше білу.
|
Сабақ барысы
|
Сабақтың жоспарланған кезеңдері
|
Сабақтағы жоспарланған іс-әрекет
|
Ресурстар
|
Басталуы
0-3 мин
|
Ұйымдастыру кезеңі
Сәлемдесу. Үй жұмысын тексеру
Саралау тәсілі «Диалог және қолдау көрсету»
Белсенді оқу әдісі. «Нұсқау беру және айту»
Біздер қандай бөлімді өтіп жатырмыз? Өткен сабақта қандай тақырыпты өттік? Қандай мақсаттарға қол жеткіздік? Сіздің ойыңызша өткен сабақтағы материалдарды өмірде қолдануға бола ма? Ендеше біздің бүгінгі мақсатымыз қандай болмақ?
Сұрақтарға жауап алу арқылы сабақтың тақырыбы, жоспары жарияланады және оқушылармен бірлесе отырып оқу мақсаттары анықталады.
ҚБ: «мұғалімнің мадақтамасы»
|
1-2 слайдтар
|
3-6 мин
7-10 мин
10-22 мин
22-25 мин
25-38 мин
36-38
38-40
|
Өткен білімді өзектендіру:
“Үшбұрыштар” тақырыбы бойынша теориялық материалдарды қайталау.
Оқыту мен оқу әдіс тәсілі: Жеке жұмыс
Саралау тәсілі «Қорытынды»
Белсенді оқу әдісі. «Бекіту және қолдануға енгізу»
«Аяқталмаған жазылым» (оқушылардың білімді жүйелеу мақсатында әзірленген тапсырмалардағы көп нүктелердің орнына қажетті сөздерді ұсынылған парақтарға жазулары керек)
Бағалау критерийі: Білім алушы
Үшбұрыштарды шешу теоремаларын анықтайды
Ойлау дағдысының деңгейі: білу және түсіну
Үшбұрыштың ..... қарама-қарсы үлкен бұрышы, үлкен бұрышына қарама-қарсы .... орналасқан (үлкен қабырғасына; үлкен қабырғасы)
Үшбұрыштың қабырғалары… бұрыштарының синустарына пропорционал (қарама-қарсы). Ол қатынастардың әрқайсысы ... -не тең (осы үшбұрышқа сырттай сызылған шеңбердің диаметрі).
Үшбұрыштың кез-келген қабырғасының квадраты ... қалған екі қабырғасының квадраттарының қосындысына тең (осы қабырғалармен олардың арасындағы бұрыштың косинусына екі еселенген көбейтіндісінсіз алынған).
Косинустар теоремасын жалпы түрде ... теоремасы деп те атайды. (Пифагор)
Үшбұрыштарды шешу дегеніміз: берілген негізгі .... бойынша үшбұрыштың басқа үш элементін табу. Бұл жерде берілген .... ең болмағанда біреуі ... болуы тиіс (үш элементі, үш элементтің, қабырға)
Үшбұрышты шешу үшін қандай теоремаларды білу керек? (синустар теоремасын, косинустар теоремасын)
ҚБ: «мұғалімнің мадақтамасы» интербелсенді тақтада дұрыс жауабы көрсетіледі, өздерін тексеріп сабақ мақсатына жету деңгейлерін бағалайды
Оқыту мен оқу әдіс тәсілі: Жеке жұмыс
Саралау тәсілі «Дереккөздер»
Белсенді оқу әдісі: «Тарих беттерінен тыңдалым» (тыңдалым арқылы таным сауаттылығын арттырып, білімдерін жалпылау мақсатында, мәтінді оқи отырып «тұжырымдамалық органайзер» ден тұжырым картасын толтыра отырады.)
Бағалау критерийі: Білім алушы
Үшбұрыштарды шешу теоремаларын анықтайды;
Ойлау дағдысының деңгейі: білу және түсіну
Барлығы аудиожазбадағы ақпараттан негізгі деректерді теріп тұжырым картасына түсіреді.
Косинус теоремасы ежелгі гректерге белгілі болған. Евклид элементтерінің екінші кітабының 12 және 13 аңыздарында үшбұрыштың сүйір және доғал бұрышқа қарсы қабырғаларының квадраты туралы мәселе қарастырылады.
Үндістандағы ғалымдар кез-келген үшбұрыштардың тұжырымдамасын тік бұрышты үшбұрыштардың шешіміне алып келді және синустар теоремасын қажет етпеді және оны білмеді.
Тікелей жазықтық үшбұрыштары үшін косинус теоремасын араб астрономы және математигі Абу-л-Вафа (940 - 998) тұжырымдады. Сәл кейінірек белгілі ортаазиялық ғалым энциклопедист Аль-Беруни (973 - 1048) осы теореманы тұжырымдайды және қолданады.
Еуропада косинус теоремасын әйгілі француз алгебрасы Франсуа Вьет (1540 - 1603) шынымен бағалады және жүйелі түрде қолданды.
Синустар туралы теореманы алғаш рет мұғалім Әл-Беруни, ирандық математик Ибн-Ирак тұжырымдады деп саналады. Бұл теореманың дәлелі Аль-Берунидің еңбектерінде де кездеседі.
Косинус теоремасы өзінің қазіргі формасын 1801 жылы француз математигі Лазар Карнодан алды: косинустар мен синустар теоремалары өзара байланысты. Олардың әрқайсысынан сәйкес тригонометриялық қатынастарды орындау арқылы екіншісін шығаруға болады.
Тұжырым картасы
тұжырым
|
жауабы
|
Көрнекті археолог Әл-Беруни синус теоремасын ... ғасырда шығарды.
|
XI
|
Еуропалық математиктер оны ... ғасырда қолдана бастады.
|
XVI
|
Евклид элементтерінде ..... теоремасы геометриялық тұрғыдан дәлелденді
|
Косинустар теоремасы
|
Косинустар теоремасы ....... және ... ғасырда ауызша тұжырымдалған
|
Француз математигі Франсуа Виет, 16 ғасыр
|
Косинустар теоремасын ... және жылы заманауи түріне келтірді
|
Француз математигі Лазаре Карно 1801 ж.
|
|
|
ҚБ: «мұғалімнің мадақтамасы» интербелсенді тақтадан өздерін тексереді
Қолданбалы есептер
Оқыту мен оқу әдіс тәсілі: Топтық жұмыстар /7мин әзірлікке 5 мин қорғауға/
Саралау тәсілі «Жіктеу»
Белсенді оқу әдісі. «Екі мұрагер мен үш елші» (1—4 дейін нөмірленген парақшалар үлестіріледі. Өз санына сәйкес топқа жинақталады. Топта ұсынылған ақпаратпен танысып, есепті талдайды, кейін орындығында «мұрагер», «бағалаушы мұрагер» сөздері бар екі оқушы орнында қалады да, орындықтарында «елші» сөзі бар үш оқушы басқа үш топтарға бөлініп кетеді. Топта қалған екі оқушының бірі бағалаушы болады, екіншісі келген үш елшімен бірге өз жұмыстарын таныстырады)
Бағалау критерийі: Білім алушы:
Үшбұрыштарды шешу теоремаларын анықтайды;
Косинустар теоремасын, синустар теоремасын қолданбалы есептер шығаруда қолданады;
Үшбұрыштарды шешу теоремаларын қолданып өмірмен байланысты күрделі есептерді шешеді.
Ойлау дағдысының деңгейі: білу және түсіну, қолдану
Барлығы қолданбалы есептер шығарады;
№1 Топ
Геодезияда қолданылуы
Үшбұрыштарды шешуді жие қолданатын мамандықтар бар. Кез-келген құрылысты бастар алдында, геодезистер бірінші болып сол жерге барып, ауданның жоспарын алып, рельефті сипаттайды. Жобалаушы ұйымдар жоба бекітер алдында геодезисттер бұрыштарды өлшеп, үшбұрыштарды шешеді, қазықтар қойып жобаны бекітеді.
Тапсырмасы:
Өзен арқылы А нүктесінен В нүктесіне дейін көпір салу керек. Инженер А нүктесінен С нүктесіне дейінгі қашықтық 100 м, ал АВС үшбұрышының А бұрышы 96,5°, ал В бұрышы 46,8°-ке тең екенін анықтады.. Көпірдің ұзындығы қандай болады?
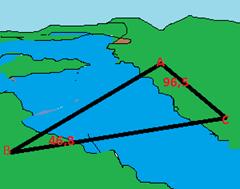
Дескриптор: Білімалушы
-С бұрышының шамасын үшбұрыштың ішкі бұрыштарының қосындысын пайдаланып анықтайды
- синустар теоремасын қолданып, теңдеу құрады;
- есептеулер жүргізеді;
- белгісізді табады.
№2 Топ
Геодезияда қолданылуы
Үшбұрыштарды шешуді қажетті қашықтықты тікелей өлшемей-ақ анықтау үшін қолданатын «маркшейдерлер» бар. Олар шахталардағы, туннельдердегі, метрополитендегі және басқа жер асты кеніштеріндегі осындай мәселелерді шешетін мамандар.
Тапсырмасы:
Аралықтары 50 м болатын А және В екі нүктеден бөктердің ең биік нүктесі сәйкесінше 50º және 30º бұрыштармен көрінеді. Егер адамның биіктігі h = 1,60 м болса, тау бөктерінің биіктігін табыңыз.
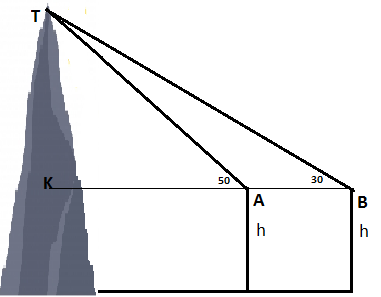
Дескриптор: Білім алушы
- АТВ үшбұрышының бұрыштарын үшбұрыштың ішкі бұрыштарының қосындысын пайдаланып анықтайды
-синустар теоремасын қолданып, теңдеу құрады;
- ТА-ның мәнін табады;
-ТАК үшбұрышына синустар теоремасын қолданады
-есептеулер жүргізеді;
- белгісізді табады.
№3 топ
Үшбұрышты шешудің навигацияда қолданылуы
Навигация теңіздегі бағытты және қашықтықты анықтау мәселелерін шешеді. Навигациялық аспаптарды, жағалаудағы және өзгермелі бағдарларды қолданып, кеменің теңіздегі орнын анықтау әдістері. Кемені басқару және ақаусыз жүргізу мәселелерін шешеді.
Кемежүргізуші мамандар картографиялық және нақты математикалық білімнің негізінде кемеде жүзушілердің өмір қауіпсіздігін сақтай алады.
Тапсырма:
Маяк қараушысы маяктың жоғарғы қабатынан балықшылар қайығын 30° және ескек қайықпен жүзіп жүргендерді 700 бұрыштан көреді. Маяктың биіктігі 100,2 м болса екі қайықтың ара қашықтығы қандай болғаны?
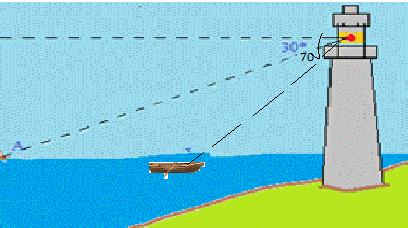
Дескриптор: Білім алушы
- 30°-қа қарсы жатқан катеттің гипотенузаның жартысына теңдігін қолданады;
- үшбұрыштың ішкі бұрыштарының қосындысын пайдаланады;
- синустар теоремасын қолданады;
- пропорция құрады;
- белгісізді табады.
№4 топ
Үшбұрышты шешудің астрономияда қолданылуы
Ежелгі уақытта адамдар тригонометрияны төбелері жұлдыздар болатын аспандағы қиялдағы үшбұрыштарды өлшеуді үйренді. Қазір тригонометрия тіпті ғарыш кемелері арасындағы қашықтықтарды өлшеу үшін қолданылады.
Тапсырмасы:
Астроном өзінің көзқарасы бойынша планетаның Күннен максималды қашықтықта болатын уақытты таңдады. Планета мен Күн арасындағы өлшеу бұрышы 38,5° құрайды. Күннің Жерден 148 800 000 км қашықтықта орналасқандығы белгілі. Күннен планетаға дейінгі арақашықтық қанша?
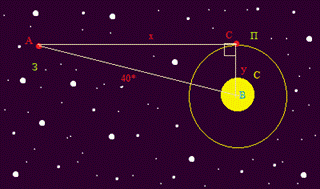
Дескриптор: Білім алушы
- тікбұрышты үшбұрыштың ішкі бұрыштарының қосындысын пайдаланады;;
- - синустар теоремасын қолданады;
- пропорция құрады;
- белгісізді табады.
ҚБ: «Екі жұлдыз бір тілек» Әр топтағы бағалаушы мұрагерлер бағалайды
Өмірде қолданылуы туралы мысалды қалай жеткізе білгенін
Есептің берілгенімен шығарылуын қаншалықты түсіндіре алғанын
Сергіту сәті: «Матростар» (жұптастыру мақсатында) (барлығы орындарынан тұрып жүзу қимылын жасайды. «ас» командасы бойынша төртеуден тұра қалып қасықпен ас ішуді көрсету, қайта жүзу, «қайыққа» командасы бойынша бесеуден тізбектеліп тұра қалып ескекпен жүзуді көрсету, қайта жүзу, «палуба тазарту» командасы бойынша екеуден тұра қалып еден жууды көрсетеді.) Сол екеуден тұра қалғандар жұптасады.
Оқыту мен оқу әдіс тәсілі: Жұптық жұмыс /Оқулықтан/
Саралау тәсілі «Қарқын»
Белсенді оқу әдісі. «Қорытынды шығару және есте сақтау» (өз жұбымен есепті талдап, шығарып нәтижесін қорытындылайды.)
Бағалау критерийі: Білім алушы
Үшбұрыштарды шешу теоремаларын анықтайды;
Косинустар теоремасын, синустар теоремасын қолданбалы есептер шығаруда қолданады;
Үшбұрыштарды шешу теоремаларын қолданып өмірмен байланысты күрделі есептерді шешеді.
Ойлау дағдысының деңгейі: қолдану, жоғары деңгей дағдылары
№3.45
Шамасы жағынан тең екі күш бір-бірімен 720 бұрыш жасай отырып, бір нүктеге әсер етеді. Егер теңәрекетті күштің шамасы 120Н болса, осы күштерді табыңыз.
Дескриптор: Білім алушы
- Есептің берілгені бойынша суретін салады;
- векторлардың параллелограмм ережесін қолданады;
-параллелеограмм қасиеттерін қолданады;
-косинустар теоремасын қолданады;
-күштерді табады.
№3.46
Шамалары 100Н және 200Н күштер бір бірімен 500 бұрыш жасай отырып, бір нүктеге әрекет етеді. Тең әрекетті күштің шамасын және оның берілген күштермен жасайтын бұрыштарын табыңыз.
Дескриптор: Білім алушы
- Есептің берілгені бойынша суретін салады;
- векторлардың параллелограмм ережесін қолданады;
-параллелеограмм қасиеттерін қолданады;
-косинустар теоремасын қолданады;
-теңәрекетті күшті табады;
-синустар теоремасын қолданады;
-пропорция құрады;
-бұрыштарды табады.
ҚБ: «Ойлан – жұптас – бөліс». Интербелсенді тақтада дұрыс жауап ұсынылады, өздерін тексеріп бағалайды
Рефлексия
Мен бүгін ... қайталадым
Мен үшін ... қызықты болды
Маған қиындық тудырғаны .... болды
Маған .... қайталау керек екен
Бағалау
Үйге тапсырма Оқулықтан №3.43
Дескриптор: Білім алушы
- Берілгені бойынша суретін салады;
- Косинустар теоремасын қолданады;
- белгісіз қабырғаны табады;
-синустар теоремасын қолданады;
- пропорция құрады;
- белгісіз бұрышты табады.
- үшбұрыштың ішкі бұрыштарының қосындысын пайдаланады;
-ауданның формуласын қолданады.
|
Үлестірме материал және
3 слайд
Аудиожазба
Үлестірме материал «тұжырым картасы»
https://cutt.ly/TfDAVZe
Жауаптарға сәйкес
4-5 слайд
Журнал «Математика в школе» 1995г
«Геометрия в древних практических задачах»
есептердің жауаптары үлесиірмеде
Ә.Н.Шыныбеков
Атамұра – 2019
119 бет
Слайд 6-7
Есептердің шығарылуы жауабымен
|
Саралау – Сіз қандай тәсілмен көбірек қолдау көрсетпексіз? Сіз басқаларға қарағанда қабілетті оқушыларға қандай тапсырмалар бересіз?
|
Бағалау – Сіз оқушылардың материалды игеру деңгейін қалай тексеруді жоспарлап отырсыз?
|
Денсаулық және қауіпсіздік техникасын сақтау
|
Қолданылатын саралау тәсілдері: «диалог және қолдау көрсету», «қорытынды», «дереккөздер». «жіктеу», «қарқын»
Жие қолданатын -«жіктеу»
Қабілетті оқушыларға топта көшбасшы болу, күрделілігі жоғары тапсырмамен қамтамасыз ету.
|
Сұрақтар қою арқылы, «аяқталмаған жазылым» әдісін қолдану арқылы анықтама, теоремаларды білу деңгейін анықтап мадақтау арқылы бағалаймын
Топта қолданбалы есептерді шығаруын «екі жұлдыз, бір тілек» арқылы бағалатамын
Жұптық жұмыста «ойлан-жұптас-бөліс» әдісі арқылы бағалаймын
|
Топтық жұмыс алдында интер белсенді тақтаны айырып, жұптық жұмыс бітерде қосу
|
 Скачать 1.37 Mb.
Скачать 1.37 Mb.