Дәріс 9; 9 апта (2). 9таырып. арапайым блшектерге жіктеу арылы рационал функцияларды интегралдау. Тригонометриялы функциялар мен иррационал рнектері бар арапайым интегралдарды интегралдау
 Скачать 220.8 Kb. Скачать 220.8 Kb.
|
|
9-тақырып. Қарапайым бөлшектерге жіктеу арқылы рационал функцияларды интегралдау. Тригонометриялық функциялар мен иррационал өрнектері бар қарапайым интегралдарды интегралдау Қарапайым бөлшектерді интегралдау Келесі берілген төрт бөлшек қарапайым бөлшектер деп аталады: I. 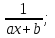 II. II. 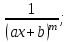 III. III. 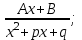 IV. IV. 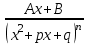 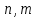 – натурал сандар ( – натурал сандар (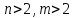 ) және ) және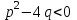 . .Алғашқы екі қарапайымбөлшектің интегралы 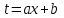 алмастыруы арқылы кестелік интегралға келтіріледі. 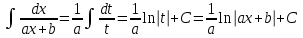 II. 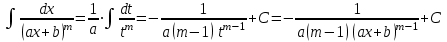 III. 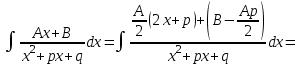 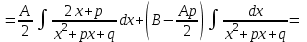 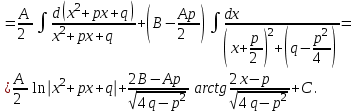 I 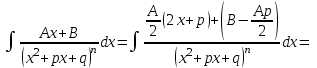 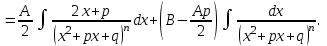 Мұнда 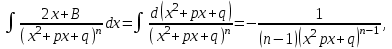 ал 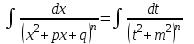 тең болады, мұндағы тең болады, мұндағы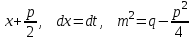 Енді 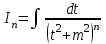 интегралы үшін келесі рекурентті формуланы қолдану керек. интегралы үшін келесі рекурентті формуланы қолдану керек. 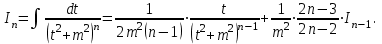 Бұл рекурентті формуланы 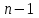 рет қолдану арқылы рет қолдану арқылы 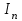 интегралын интегралын 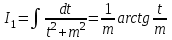 негізгі кестелік интеграл арқылы есептеуге болады. 1-мысал. 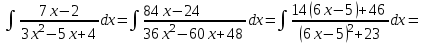  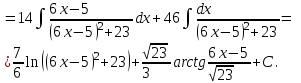 Рационал функцияларды интегралдау Дұрыс рационал бөлшектерді интегралдау үшін оларды төмендегідей қарапайым бөлшектерге жіктеу керек: 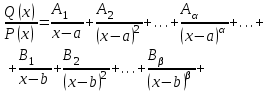 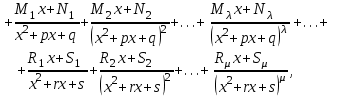 мұндағы 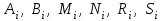 – тұрақты сандар. – тұрақты сандар.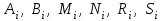 шамаларының мәндерін анықтау үшін белгісіз коэффициенттер әдісін қолданыламыз (екі көпмүше тең болуы үшін х-тің бірдей дәрежесіндегі коэффициенттердің тең болуы қажетті және жеткілікті). шамаларының мәндерін анықтау үшін белгісіз коэффициенттер әдісін қолданыламыз (екі көпмүше тең болуы үшін х-тің бірдей дәрежесіндегі коэффициенттердің тең болуы қажетті және жеткілікті). Бұрыс рационал бөлшектер үшін алдын ала бүтін бөлігін шығарып алуымыз керек. 2-мысал. 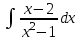 интегралын есептеу керек. интегралын есептеу керек. Шешуі: Интеграл атындағы өрнек бөлімінің екі нақты түбірі бар дұрыс рационал бөлшек, олай болса 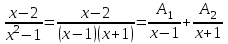 тең екендігін аламыз. Осыдан 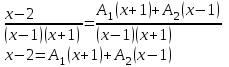 x айнымалысының бірдей дәрежелерінің алдындағы коэффициенттерін теңестірсек 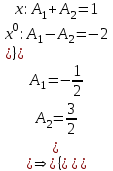 Табылған 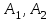 коэффициентін орнына қойсақ коэффициентін орнына қойсақ 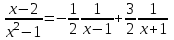 Сонда 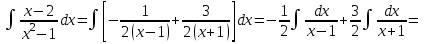 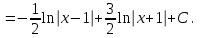 3-мысал. 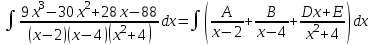 . .Ортақ бөлімге келтіре отырып, алымдарын теңестіреміз: 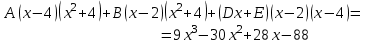 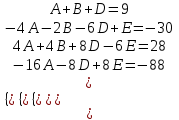 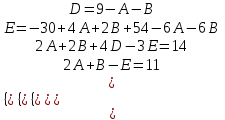 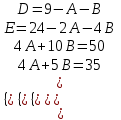 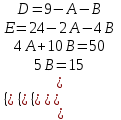 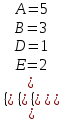 Сонымен 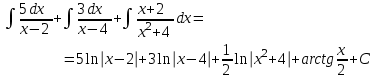 . .Иррационал функцияларды интегралдау 1. 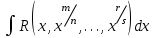 интегралын қарастырайық. Осы интеграл интегралын қарастырайық. Осы интеграл 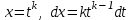 алмастыруын қолдану арқылы рационал функцияның интегралына келтіріледі, мұндағы 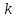 саны саны 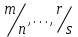 бөлшектерінің ортақ бөліміне тең. бөлшектерінің ортақ бөліміне тең.4-мысал. 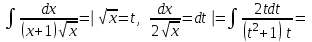 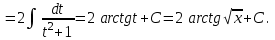 2. 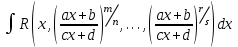 интегралын қарастырайық. Осы интеграл интегралын қарастырайық. Осы интеграл 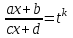 алмастыруын қолдану арқылы рационал функцияның интегралына келтіріледі, мұндағы алмастыруын қолдану арқылы рационал функцияның интегралына келтіріледі, мұндағы 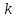 саны саны 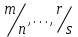 бөлшектерінің ортақ бөліміне тең. бөлшектерінің ортақ бөліміне тең.5-мысал. 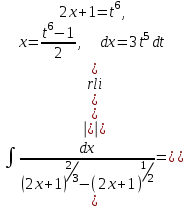 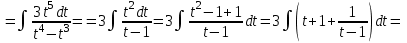 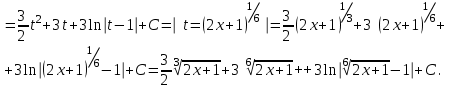 6-мысал. 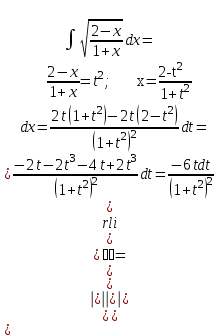 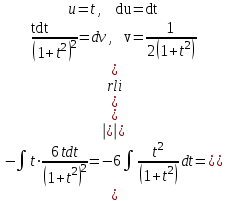 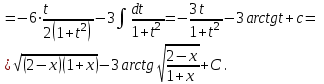 Кейбір тригонометриялық функцияларды интералдау 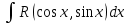 Интегралдың бұл түрін есептеу үшін 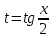 алмастыруы қолданылады мұны универсал алмастыру деп аталады Бұл арқылы алмастыруы қолданылады мұны универсал алмастыру деп аталады Бұл арқылы 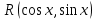 . Функциясы жаңа . Функциясы жаңа 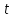 айнымалысының рационал функциясына түрленеді. айнымалысының рационал функциясына түрленеді.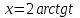 , , 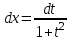 . .Тригономатриядан белгілі формулалар бойынша 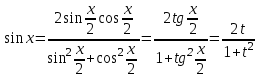 , ,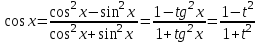 Сондықтан 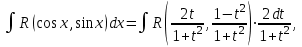 мұндағы интегралданатын функция 7-мысал. 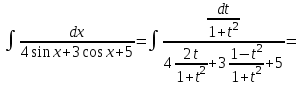 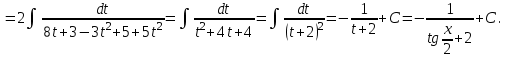 Кейбір жағдайларда осындай алмастырулар күрделі есептеулерге кездестіреді, сондықтан басқа алмастырулар қолдануға болады. Солардың кейбіреулерін қарастырайық: 1) 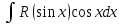 болса, онда болса, онда 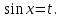 8-мысал. 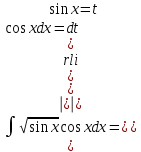 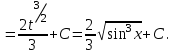 2) 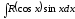 болса, онда болса, онда 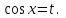 9-мысал. 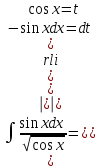 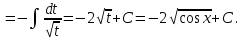 3) 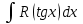 болса, онда болса, онда 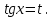 10-мысал. 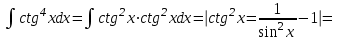 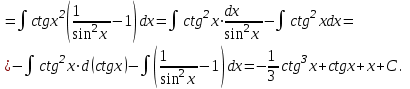 4) 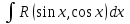 интегралында интегралында 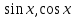 функциялары тек жұп дәрежелерімен берілсе, онда функциялары тек жұп дәрежелерімен берілсе, онда 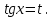 11-мысал. 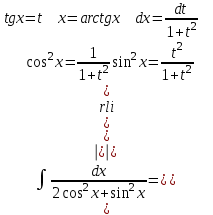 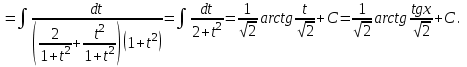 5) 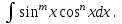 а) 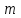 тақ болса, онда тақ болса, онда 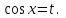 12-мысал. 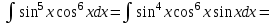 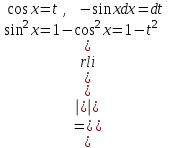 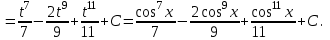 ә) 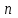 тақ болса, онда тақ болса, онда 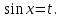 13-мысал. 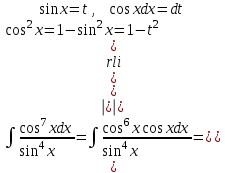 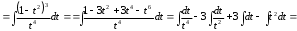 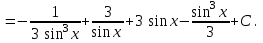 б) 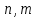 жұп, теріс емес болса онда жұп, теріс емес болса онда 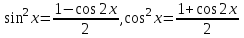 формулалары қолданылады. формулалары қолданылады. 14-мысал. 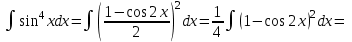 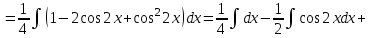 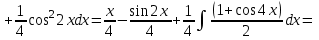 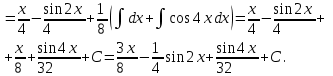 в) 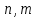 жұп, ең болмаса біреуі теріс болса, онда жұп, ең болмаса біреуі теріс болса, онда 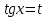 немесе немесе 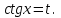 15-мысал. 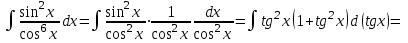 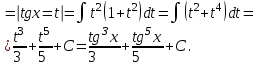 6) Әртүрлі аргументтердің синус және косинустарының көбейтіндісінің интегралы берілсе, онда бұл жағдайда төмендегі 3 формуланың біреуін қолданамыз: 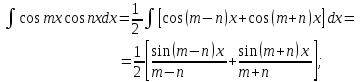 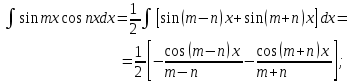 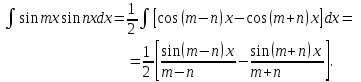 16-мысал. 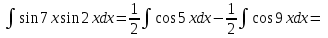 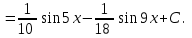 |
