Математическое моделирование. задание на 06.08. последний docx. А для получения алгебраической форме домножим числитель и знаменатель данной дроби
 Скачать 51.4 Kb. Скачать 51.4 Kb.
|
|
Задание № 1 А) Для получения алгебраической форме домножим числитель и знаменатель данной дроби: 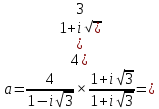 Для получения тригонометрической формы: А=r(isin(ϕ)+cos(ϕ)) Находим сначала r= 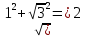 , , 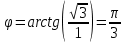 тогда в тригонометрическом виде: тогда в тригонометрическом виде:Тригонометрическую получаем соответственно : 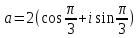 Б) Уравнение 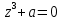 Сначала переведем уравнение 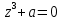 в вид в вид 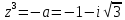 В тригонометрическом виде 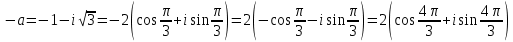 Все корни третьей степени из числа Z находим по формуле: 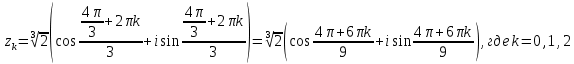 Тогда корни :  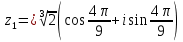 ; ; 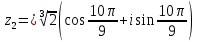 ; ;  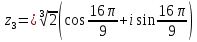 Задание №2 Представим заданную функцию w=f(z) , где z=x+iy в виде w=u(x,y) +iv(x,y) Проверить – является ли она аналитической, если ДА , то найти ее производную в точке z=1-i. W = 2 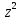 -iz -iz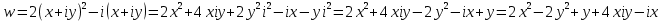 U= 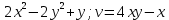 Проверим условие Коши – Римана, для этого найдем частные производные: Теорема. Пусть функция f(z)=u(x,y)+iv(x,y) определена в некоторой окрестности точки z =(x0,y0)∈D, причем в этой точке функции v(x,y) и v(x,y) непрерывно дифференцируемы по x и y. Тогда для дифференцируемости функции комплексного переменного f(z) необходимо, а при существовании полных дифференциалов du(x,y), dv(x,y) и достаточно, чтобы в этой точке =(x0,y0)∈D имели место условия Коши-Римана (иногда их называют условиями Эйлера-Даламбера):∂u/∂x=∂v/∂y,∂u/∂y=−∂v/∂x. 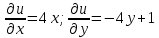 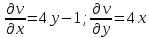 Таким образом : 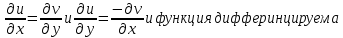 Заметим, что f′(z0) может быть представлена одной из следующих форм:f′(z0)=∂u/∂x+i∂v/∂x=∂v/∂y−i∂u/∂y=∂u/∂x−i∂u/∂y=∂v/∂y+i∂v/∂x. Если же дана зависимость w=f(z), то после проверки выполнения условий производную можно найти непосредственным дифференцированием:w′=df(z)/dz. Найдем производную 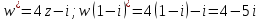 Задание № 3 Используя теорему о вычетах , вычислить интеграл по контуру С против часовой стрелки 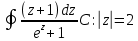  |Z| = 2 – окружность радиуса 2 с центром в начале координат. Найдём особые точки подынтегральной функции. |Z| = 2 – окружность радиуса 2 с центром в начале координат. Найдём особые точки подынтегральной функции.  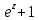 =0 =0 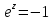 z=ln(-1)= 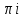 Используя разложение : 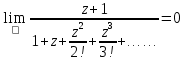 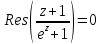 в окрестностях точки pi в окрестностях точки pi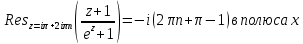 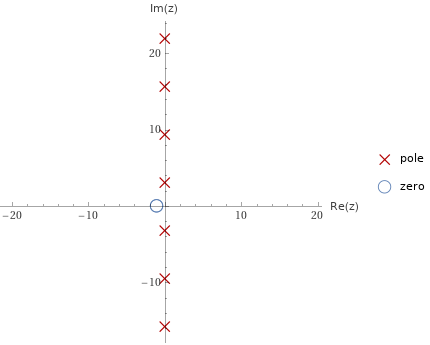 Задание № 4 Найти оригинал f(t), которому соответствует изображение Лапласа F(p): 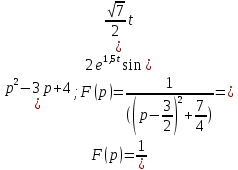 Задание № 5 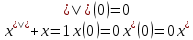 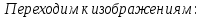 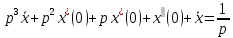 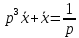 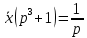 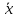 = =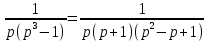 Разложим эту рациональную дробь на простейшие дроби: B=-1-C 1+C+C+D=0 1+2C+D=0 D=-B 1+2C-B=0 1+2C-(-1-C)=0 1+2C+1+C=0 3C= - 2 C= 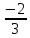 A+B+C=0 -B+C+D=0 C+2D=0 B+D=0 D=  B+D=0 B=-D =  1+B+C=0   x(p)= 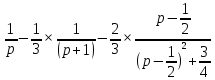 ; ; 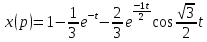 Задание № 6 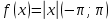 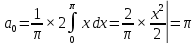   При m=2n  При m=2n-1  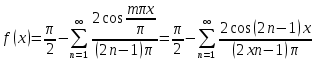 Задание № 7 Интегрирование по первой четверти данной окружности означает, что путь интегрирования начинается от точки (R,0) декартовой системы координат (соответствующей значению t=0 параметра) до точки (0,R) (соответствующей значению t= 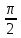 параметра) по дуге окружности. Если возвести обе части равенств x=Rcos t и y=Rsin t в квадрат и сложить их, то получим более привычное уравнение окружности x2+y2=R2. параметра) по дуге окружности. Если возвести обе части равенств x=Rcos t и y=Rsin t в квадрат и сложить их, то получим более привычное уравнение окружности x2+y2=R2.Имеем: dx=-Rsintdt, dy=Rcostdt. Получим 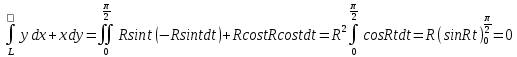 Можно также предложить и второе решение. Замечаем, что данный интеграл по отрезку {0 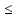 x x R, y=0} равен нулю (y=0 и dy=0). То же самое справедливо и для отрезка {0 R, y=0} равен нулю (y=0 и dy=0). То же самое справедливо и для отрезка {0 y y R, x=0} (здесь x=0 и dx=0). Добавляем эти отрезки к кривой L (четверь окружности) и получаем тот же самый интеграл, но по замкнутому контуру L1. R, x=0} (здесь x=0 и dx=0). Добавляем эти отрезки к кривой L (четверь окружности) и получаем тот же самый интеграл, но по замкнутому контуру L1.Применяя к этому криволинейному интегралу формулу Грина (P=y, Q=x), получим  Для нашего случая получим, под двойным интегралом (P'y=1, Q'x=1) (1-1)=0. Значит интеграл равен нулю.  Задание №8 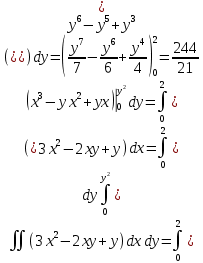 |
