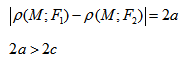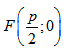Лекции. Лекция 4.2.Кривые второго порядка (1). Окружность Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром

• Название: Окружность Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром
• Анкор: Лекции
• Дата: 25.10.2022
• Размер: 0.89 Mb.
• Имя файла: Лекция 4.2.Кривые второго порядка (1).docx
• Тип: Лекция; #753280

Лекция 4.2. Кривые второго порядка

1. 
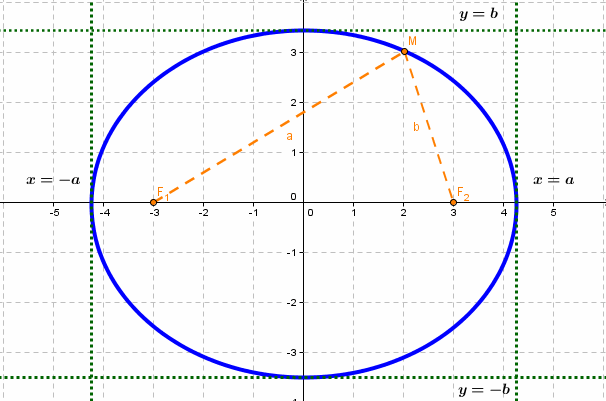
   Окружность
   

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Р ассмотрим окружность в прямоугольной декартовой системе координат.

Если точка С(а,b) – центр окружности, R – радиус окружности, то общее уравнение окружности имеет вид:



Если центр окружности совпадает с началом координат, то мы имеем каноническое уравнение окружности:

х² + у²=R²

Примеры:

1) Написать уравнение окружности радиуса R = 5 с центром в начале координат:

Решение: Непосредственной подстановкой значения радиуса в каноническое уравнение окружности х² + у² = R² получим: х² + у² = 5²или х² + у² = 25.
2) Написать уравнение окружности радиуса R = 3с центром в точке С(-1;2):

Решение: Непосредственной подстановкой значения радиуса и значение координат точки С в общее уравнение окружности (х-а)² + (у-b)² = R², получим: (х-(-1))² + (у-2)² = 3² или

(х+1)² + (у-2)² =9.

2. 
   Эллипс
   

Эллипс- множество точек на плоскости, сумма расстояний от каждой из которых до двух данных точек F₁ и F₂ есть величина постоянная, большая расстояния между этими точками.

Эти точки : F₁ и F₂ - фокусы.  

2с - фокальное расстояние, F1(-c;0) - левый фокус, F2(c;0) - правый фокус.

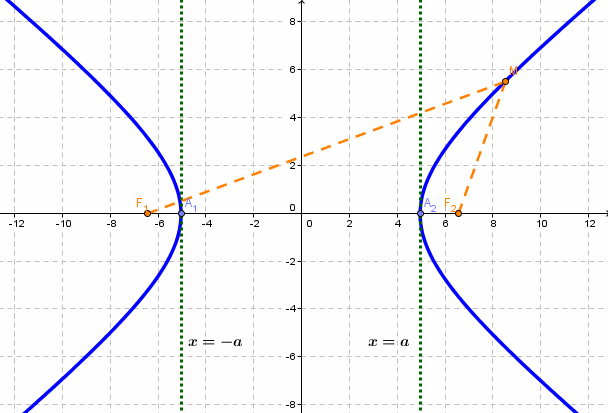
 Каноническое уравнение эллипса с центром симметрии в начале координат:



2а - большая ось эллипса, 2b - малая ось эллипса.

а - большая полуось эллипса, b - малая полуось эллипса.

Если a = b, то имеем окружность с радиусов R = a = b:



Если центр эллипса находится не в начале координат, а в некоторой точке C(x₀;y₀),  оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид: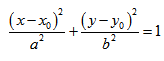

 

Эксцентриситет - число, равное отношению  фокального расстояния к большей полуоси:

 

Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.

3. 
   Гипербола
   

Гипербола - множество точек на плоскости, для каждой из которых абсолютная величина разности расстояний до двух данных точек F₁ и F₂ есть величина постоянная, меньшая расстояния между этими точками.

F₁ и F₂ - фокусы.

2с - фокальное расстояние, F1(-c;0) - левый фокус, F2(c;0) - правый фокус. А1(-а;0),  А2(а;0) - вершины.

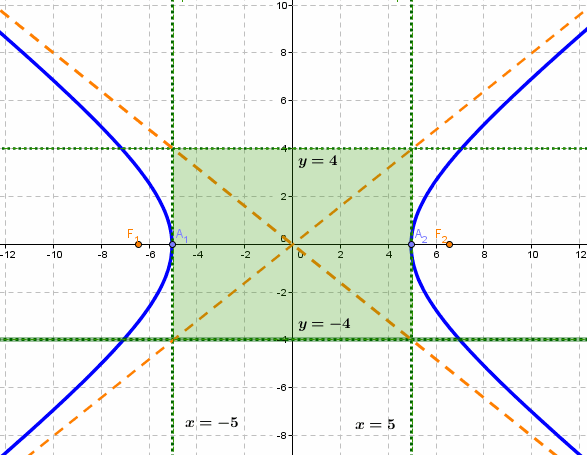
Каноническое уравнение гиперболы с центром симметрии в начале координат:

 

x - действительная ось, y - мнимая ось.

а - действительная полуось,   b -  мнимая полуось.

Если центр гиперболы находится в некоторой точке C(x₀;y₀),  оси симметрии параллельны осям координат, то каноническое уравнение имеет вид: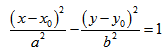



Эксцентриситет гиперболы - число, равное отношению фокусного расстояния к действительной полуоси.



Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.

Директриса гиперболы - прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.

f₁ -  правая директриса,   f₂ -  левая директриса.

Уравнения директрис:



Порядок построения гиперболы:

1. Строим прямоугольник со сторонами 2a и 2b.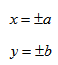



2. Провести асимптоты гиперболы - диагонали построенного прямоугольника.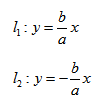



3. Строим гиперболу с вершинами в точках А₁(-а;0),  А₂(а;0).

4. 
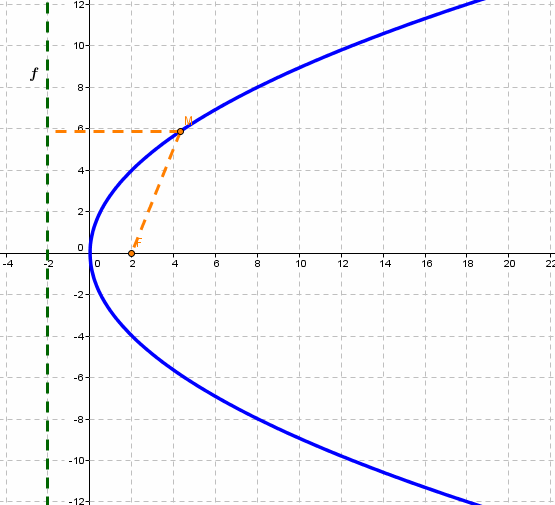
   Парабола
   

Парабола - множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.

F - фокус параболы, f - директриса параболы. 

р - фокальное расстояние  Фокус параболы: Директриса параболы:  Каконическое уравнение параболы:

Домашнее задание: практическое занятие №11