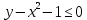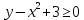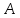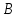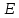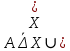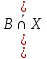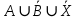Основы дискретной математики и логики .1. Множества и операции над ними. Решение. Изобразим сначала сами множества и это множество точек, лежащих ниже параболы, включая границу
 Скачать 71.14 Kb. Скачать 71.14 Kb.
|
|
1. Пусть 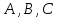 – множество точек плоскости, координаты которых удовлетворяют условиям – множество точек плоскости, координаты которых удовлетворяют условиям 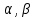 и и 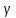 соответственно. Изобразите в системе координат соответственно. Изобразите в системе координат 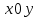 множество множество  , полученное из множеств , полученное из множеств  и и 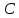 по формуле по формуле  . .
Решение. №1. Изобразим сначала сами множества  и и 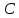 : :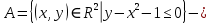 это множество точек, лежащих ниже параболы это множество точек, лежащих ниже параболы  , включая границу. , включая границу.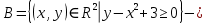 это множество точек, лежащих выше параболы это множество точек, лежащих выше параболы 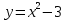 , включая границу. , включая границу.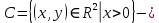 это полуплоскость, лежащая левее вертикальной прямой это полуплоскость, лежащая левее вертикальной прямой  , не включая границу. , не включая границу.
Ответ: Тогда множество  имеет вид имеет вид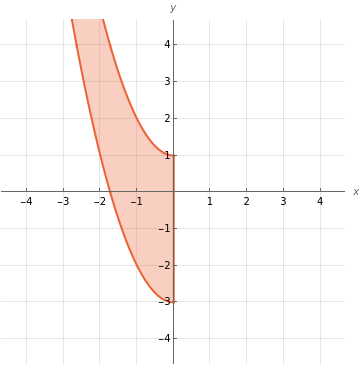 2. Выяснить взаимное расположение множеств  если А, В, Х – произвольные подмножества универсального множества если А, В, Х – произвольные подмножества универсального множества 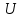 . .
Решение. С помощью диаграмм Эйлера-Венна определим множества 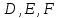 . Множества . Множества  находятся в общем положении, т. е. имеем следующую диаграмму находятся в общем положении, т. е. имеем следующую диаграмму Тогда множество  и и 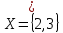 . Следовательно, . Следовательно, 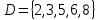 . .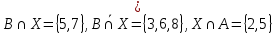 . Следовательно, . Следовательно, 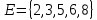 . .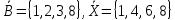 . Следовательно, . Следовательно, 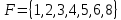 . .Ответ: 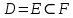 . . | ||||||||||||||||||||||||||||||||