биореология. A. Градиент скорости, площадь взаимодействующих слоев, коэффициент вязкости
 Скачать 217.39 Kb. Скачать 217.39 Kb.
|
|
З А Д А Н И Е № 1 Выберите параметры, которые входят формулу Ньютона для силы внутреннего трения. A. Градиент скорости, площадь взаимодействующих слоев, коэффициент вязкости. B. Радиус сосуда, разность давлений, коэффициент вязкости, гидравлическое сопротивление. C. Площадь взаимодействующих слоев, разность давлений, толщина сосуда, скорость. D. Гидравлическое сопротивление, коэффициент вязкости, скорость. E. Разность давлений, радиус сосуда, скорость. З А Д А Н И Е № 2 Выберите параметры, которые входят формулу Пуазейля. A. Градиент скорости, длина сосуда, коэффициент вязкости. B. Радиус сосуда, длина сосуда, разность давлений, коэффициент вязкости. C. Радиус сосуда, длина сосуда, площадь взаимодействующих слоев, коэффициент вязкости. D. Длина сосуда, площадь взаимодействующих слоев, коэффициент вязкости. E. Разность давлений, плотность крови, длина сосуда, коэффициент вязкости. З А Д А Н И Е № 3 Выберите параметры, которые входят формулу для расчета числа Рейнольдса. A. Площадь взаимодействующих слоев, скорость течения жидкости, плотность жидкости, коэффициент вязкости. B. Скорость течения жидкости, плотность жидкости, диаметр сосуда, коэффициент вязкости. C. Градиент скорости, плотность жидкости, коэффициент вязкости. D. Скорость течения жидкости, разность давлений, диаметр сосуда, длина сосуда. E. Градиент скорости, плотность жидкости, коэффициент вязкости, диаметр сосуда. З А Д А Н И Е № 4 Что называют пульсовой волной? A. Волну, распространяющуюся по кровеносным сосудам (артериям, венам и т.д.) при работе сердца. B. Распространяющуюся по венам волну повышенного давления. C. Распространяющуюся по аорте и артериям волну повышенного давления, вызванную выбросом крови из левого желудочка в период систолы. D. Распространяющуюся по аорте и артериям волну, вызванную скоростью течения крови. З А Д А Н И Е № 5 От каких параметров зависит скорость пульсовой волны? A. Модуль упругости, плотность крови, толщина стенки сосуда, радиус сосуда. B. Коэффициент вязкости, плотность крови, толщина стенки сосуда, радиус сосуда. C. Градиент скорости, плотность крови, толщина стенки сосуда. D. Модуль упругости, плотность крови, число Рейнольдса, радиус сосуда. E. Коэффициент вязкости, площадь взаимодействующих слоев, толщина стенки сосуда, радиус сосуда. З А Д А Н И Е № 6 Что называют кинематической вязкостью? A. Отношение вязкости крови к вязкости воды при градиенте давления, равном единице. B. Отношение динамической вязкости жидкости к плотности жидкости. C. Отношение динамической вязкости жидкости к вязкости воды при одинаковой температуре. D. Произведение числа Рейнольдса на скорость течения жидкости. З А Д А Н И Е № 7 Выберите параметры, от которых зависит характер течения жидкости по сосудам. A. Плотность жидкости, динамическая вязкость, скорость течения жидкости, радиус сосуда. B. Плотность жидкости, длина сосуда, скорость течения жидкости, радиус сосуда. C. Градиент давления, длина сосуда, скорость течения жидкости, радиус сосуда. D. Гидравлическое сопротивление, длина сосуда, скорость течения жидкости, радиус сосуда. E. Плотность жидкости, длина сосуда, разность давлений, радиус сосуда. З А Д А Н И Е № 8 Какие значения скорости соответствуют скорости пульсовой волны в организме человека? A. 50 см/с B. 6 м/с , 9 м/с. C. 30 см/с , 20 м/с, 7 м/с. D. 20 м/с E. 5 м/с, 18 м/с. З А Д А Н И Е № 9 Как изменится гидравлическое сопротивление при увеличении площади сечения трубы в 3 раза? A. Увеличится в 1.72 раза. B. Уменьшится в 3 раза. C. Уменьшится в 4 раза. D. Уменьшится в 9 раз. E. Гидравлическое сопротивление не изменится. З А Д А Н И Е № 10 Коэффициент вязкости для ньютоновских жидкостей зависит от : A. Температуры, природы жидкости. B. Скорости ее течения, температуры, природы жидкости. C. Природы жидкости, скорости течения жидкости. D. Площади взаимодействующих слоев, природы жидкости. E. Площади взаимодействующих слоев, градиента скорости. З А Д А Н И Е № 11 Сила внутреннего трения между двумя слоями жидкости, которые движутся с различными скоростями, зависит от природы жидкости, а также от: A. Скорости течения жидкости и температуры. B. Градиента скорости и площади соприкасающихся слоев. C. Скорости течения жидкости и толщины слоя. D. Скорости течения жидкости и площади соприкасающихся слоев. З А Д А Н И Е № 12 Жидкость является неньютоновской, если: A. Ее вязкость много больше вязкости воды. B. Ее вязкость много меньше вязкости воды. C. Ее вязкость зависит от градиента скорости. D. Ее вязкость не зависит от характера течения жидкости. З А Д А Н И Е № 13 Как изменяется скорость движения и расход несжимаемой жидкости при движении ее по трубе переменного сечения? A. С уменьшением сечения трубы скорость движения жидкости увеличивается, а ее расход уменьшается; B. С уменьшением сечения трубы скорость движения жидкости увеличивается, а ее расход остается неизменным; C. С уменьшением сечения трубы скорость движения и расход жидкости уменьшаются; D. С уменьшением сечения трубы скорость движения и расход жидкости увеличиваются; З А Д А Н И Е № 14 Какой физический смысл коэффициента вязкости? A. При течении вязкой жидкости, состоящей из крупных молекул, возникают силы, которые и называются коэффициентом вязкости жидкости. B. Коэффициент вязкости численно равен силе трения, возникающей между слоями единичной площади и градиенте скорости равном единице. C. Коэффициент вязкости - это отношение вязкости жидкости к вязкости дистиллированной воды при той же температуре. D. Вязкостью жидкости называют силу, с которой жидкость воздействует на стенки трубы при ее течении. З А Д А Н И Е № 15 От чего зависит гидравлическое сопротивление вязкой жидкости? A. От радиуса сосуда, вязкости жидкости, длины сосуда. B. От скорости течения, вязкости жидкости, длины сосуда. C. От разности давлений, плотности жидкости, длины сосуда. D. От разности давлений, плотности жидкости. E. От скорости течения, вязкости жидкости, числа Рейнольдса. З А Д А Н И Е № 16 Каким методом определяется вязкость крови? A. Капиллярным и ротационным. B. Методом Стокса. C. Ротационным и методом Стокса. D. Капиллярным и методом Стокса. З А Д А Н И Е № 17 Как изменяется градиент давления при движении жидкости по трубе переменного сечения ? A. Одинаковый по всей длине трубы. B. Уменьшается по направлению течения жидкости. C. Больше в трубах большего радиуса. D. Больше в трубах меньшего радиуса. З А Д А Н И Е № 18 Какую в среднем работу выполняет сердце за одну систолу? A. 3.3 Дж B. 1 Дж C. 0.68 Дж D. 5 Дж E. 33 Дж З А Д А Н И Е № 19 Какую мощность в среднем развивает сердце? A. 3.3 Вт B. 1 Вт C. 10 Вт D. 33 Вт E. 0.55 Вт. З А Д А Н И Е № 20 Гемодинамика- это: A. Раздел биомеханики, в котором исследуется движение крови по сосудистой системе. B. Раздел механики, в котором изучается движение вязкой жидкости. C. Раздел физики, в котором изучаются основы работы технических устройств, используемых при рассмотрении проблем кровообращения. D. Раздел медицины, изучающий модели кровообращения. З А Д А Н И Е № 21 В каких единицах измеряется динамическая вязкость жидкости в системе СИ? A. м  /с /сB. Стокс C. Пуаз D. Па·с E. Н/м З А Д А Н И Е № 22 Что определяется числом Рейнольдса при движении вязкой жидкости по трубе? A. Скорость течения жидкости. B. Характер течения жидкости. C. Величина отношения кинематической вязкости к динамической. D. Гидравлическое сопротивление трубы. E. Объем протекающей жидкости. З А Д А Н И Е № 23 Почему кровь является неньютоновской жидкостью? A. Это обусловлено наличием в ней форменных элементов. B. Это обусловлено тем, что для крови число Рейнольдса принимает критическое значение. C. Это обусловлено большим коэффициентом вязкости крови. D. Это обусловлено маленьким коэффициентом вязкости крови. З А Д А Н И Е № 24 Что является причиной движения крови по сосудистому руслу? A. Работа сердца. B. Всасывающее действие струи. C. Разность давлений внутри и вне сосуда. D. Разность давлений в начале и в конце сосудистого русла. E. Всасывающее действие струи и работа сердца. З А Д А Н И Е № 25 Почему скорость течения крови в капиллярах меньше в сравнении со скоростью ее движения в венах, артериях и артериолах? A. Это связано с тем, что общее сечение (просвет) капилляров максимально. B. Это связано с тем, что капилляры имеют наименьший просвет. C. Это связано с тем, что капилляры находятся очень далеко от места выброса крови (левого желудочка). D. Это связано с тем, что капилляры имеют очень большое гидравлическое сопротивление. З А Д А Н И Е № 26 При измерении давления по методу Короткова прослушиваются характерные тоны и шумы. Почему они пропадают при снижении давления в манжете ниже диастолического? A. Это связано с тем, что в этом случае не образуется стоячая волна. B. Это связано с уменьшением колебаний давления в пульсовой волне. C. Это связано с резким уменьшением работы, выполняемой сердцем. D. Это связано с тем, что течение крови через сдавленную артерию переходит от турбулентного к ламинарному. З А Д А Н И Е № 27 На что затрачивается работа, совершаемая сердцем? A. Только на преодоление сил давления. B. На преодоление сил давления и сообщение крови кинетической энергии. C. На поддержание давления в кровеносной системе. D. Только на сообщение крови кинетической энергии. З А Д А Н И Е № 28 На чем основан ультразвуковой метод измерения скорости кровотока? A. Метод основан на измерении изменения частоты ультразвуковой волны при отражении ее от пульсовой волны. B. Метод основан на измерении затухания ультразвука при прохождении его через кровеносный сосуд. C. Метод основан на измерении изменения частоты ультразвуковой волны при отражении ее от движущихся эритроцитов. D. Метод основан на измерении частоты стоячей ультразвуковой волны при движущихся эритроцитах. З А Д А Н И Е № 29 Что называют расходом жидкости? A. Это скорость жидкости, с которой она протекает через сечение трубы. B. Это масса жидкости, протекающая через сечение трубы. C. Это объем жидкости, протекающий по системе труб (сосудов). D. Это объем жидкости, протекающий через сечение трубы в единицу времени; ЗАДАЧИ З А Д А Н И Е № 1 Вычислите силу трения, действующую на S=4 кв.м. дна русла, если по нему перемещается поток воды высотой h=2м, скорость верхнего слоя воды равна 0 у дна, вязкость жидкости n=10 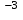 (Па · с). (Па · с).A. 0.6 мН B. 6.72 Н C. 0.3 мкН D. 320 кН E. 4.7 Н З А Д А Н И Е № 2 На каждый квадратный метр площади дна канала, по которому протекает вода действует сила 0.63 мН. Определить высоту движущегося потока воды, если скорость верхних слоев воды 0.5 м/с, а затем постепенно убывает и у дна становится равной 0. Вязкость воды 1.787·10 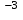 Па·с. Па·с.A. 8.5 м B. 1.42 м C. 0.79 м D. 1 м E. 0.52 м З А Д А Н И Е № 3 Скорость течения воды в широкой части горизонтальной водопроводной трубы равна 50 см/с. Какова скорость течения воды в узкой части той же трубы, диаметр которой в четыре раза меньше? A. 12.5 м/с B. 25 см/с C. 4.0 м/с D. 8.0 м/с E. 12.5 см/с ОБУЧАЮЩИЕ ЗАДАНИЯ 1. Скорость потока крови в капиллярах равна примерно v1= 30 мм/мин, а скорость потока крови в аорте v2= 45 см/с. Определить, во сколько раз площадь сечения всех капилляров больше сечения аорты. ПРИМЕР РЕШЕНИЯ Согласно уравнению неразрывности струи: S1×v1 = S2×v2, следовательно: S1/ S2 = v2/ v1 =(45 см/с)/(3 см/60 с) = 900. 2. Лекарственный раствор вводят в мышцу животного с помощью шприца, внутренний диаметр которого d1 = 10 мм, а диаметр иглы d2 = 0,5 мм. Определить скорость истечения раствора из иглы, если скорость перемещения поршня шприца равна v1 = 2,3 см/с. ПРИМЕР РЕШЕНИЯ Согласно уравнению неразрывности струи: S1×v1 = S2×v2 = следовательно: v2 = S1×v1/ S2= (d1/d2)2×v1= (10/0,5)2×2,3 см/с =920 см/с. 3. Допустим, что в двух кровеносных сосудах градиент давления одинаков, а поток крови (объемный расход) во втором сосуде на 80% меньше, чем в первом. Найти отношение их диаметров. ПРИМЕР РЕШЕНИЯ Cогласно уравнению Пуазейля: Q =(p×r4×DP)/8h×l. По условию задачи: Q2=0,2×Q1. Следовательно: Q1/Q2 =(r1/r2)4 = (d1/d2)4 =5. Т.о.: (d1/d2) = 1,5. 4. Какова должна быть разность давлений АР на концах капилляра радиуса r = 1 мм и длины L = 10 см, чтобы за время t = 5 с через него можно было пропустить объем V = 1 см3 воды (коэффициент вязкости η1 = 10-3 Па×с) или глицерина (η2 = 0,85 Па×с)? ПРИМЕР РЕШЕНИЯ Объем V=Q×t = DP×p×r4×t/8×h×l. Отсюда: DP1 = V×8×h×l /(p×r4×t) = 10-6×8×10-3×0,1/(3,14×10-12×5 = 51 (Па). DP2 = V×8×h×l /(p×r4×t) = 10-6×8×0,85×0,1/(3,14×10-12×5 = 43350 (Па). 5. Падение давления в кровеносном сосуде длины L = 55 мм и радиуса r = 1,5 мм равно 365 Па. Определить, сколько миллилитров крови протекает через сосуд за 1 минуту. Коэффициент вязкости крови η = 4,5 мПа×с. ПРИМЕР РЕШЕНИЯ Объем крови: V=Q×t = DP×p×r4×t/8×h×l = = 365×3,14×(1,5×10-3)4×60/(8×4,5×10-3×55×10-3)×106 = 175 мл. 6. При атеросклерозе, вследствие образования бляшек на стенках сосуда, критическое значение числа Рейнольдса может снизиться до 1160. Определить для этого случая скорость, при которой возможен переход ламинарного течения крови в турбулентное в сосуде диаметром 2,5 мм. Плотность крови равна ρ = 1050 кг/м3, вязкость крови равна η = 5×10-3 Пас. ПРИМЕР РЕШЕНИЯ Согласно условию перехода ламинарного течения в турбулентное: Re=r×v×d/h, откуда: v =(Reкр×h)/r×d = 1160×5×10-3/(1050×2,5×10-3) = 2,2 (м/с). 7. Определить максимальную объемную скорость протекания жидкости r=103 кг/м3 по игле шприца с внутренним диаметром D = 0,3 мм, при которой сохраняется ламинарный характер течения. Вязкость жидкости равна 1 мПа×с, критическое число Рейнольдса равна 2300. ПРИМЕР РЕШЕНИЯ Согласно определению числа Рейнольдса: v =(Reкр×h)/r×d и объемной скорости: Q= S×v = p×Reкр×h×d /4×r = 3,14×2300×10-3×0,3×10-3/4000 = 0,54×10-6 мл/с. ПРИМЕР РЕШЕНИЯ Cкорость пульсовой волны можно найти по формуле: v =ÖE×h/2×r×r, где E - модуль упругости стенок сосудов, h – толщина стенок сосудов, r - плотность крови, r – радиус просвета сосудов. Следовательно: r/h = Е/2×v2×r = = 8∙105Па/2×64м2/с2×1,05∙103 кг/м3 = 5,95. Ответ: отношение внутреннего радиуса к толщине стенки сосуда r/h = 5,95. На каждый квадратный метр площади дна канала, по которому протекает вода, действует сила 0,025 мН. Определить скорость верхних слоев воды, если высотa движущегося потока воды h= 25 м, а вязкость воды 1,2·10  Па·с. Па·с.A. 0,75 м/с; B. 0,521 м/с; C. 0,025 м/с; D. 1200 м/с; E. 1,42 м/с. 2. При стационарном потоке крови в сосуде с диаметром d1 = 4 м скорость потока равна 16 см/с. Какова скорость кровотока в сечении с диаметром d2 = 8 м? A. 8 см/с. B. 32 м/с. C. 2,5 см/с D. 4 см/с. E. 32 см/с. 3. Какая объемная скорость жидкости в трубе с диаметром 3м, если ее линейная скорость равна 5 м/с? А. 15 м3/с; В. 45 м3/с; С. 11,25 м3/с; D. 35,325 м3/с; Е. 18 м3/с. 4. Какое максимальное количество крови может пройти через аорту за 2 секунды, чтобы течение оставалось ламинарным, если радиус аорты 2см, вязкость крови 5мПа∙с, а критическое число Рейнольдса равно 2000? А. 0,314 кг; В. 0,628 кг; С. 0,128 кг; D. 0,05 кг; Е. 0,428 кг. 5. Какое гидравлическое сопротивление сосуда длиной 1 см, если его внутренний диаметр 0,2 мм, а вязкость крови 4 мПа×с? А. 10,2×1011 Па×с/м3; В. 10,2×106 Па×с/м3; С. 10,2×107 Па×с/м3; D. 0,8×1016 Па×с/м3; Е. 2×1011 Па×с/м3. 6. Жидкость является неньютоновской, если: A. Ее вязкость много больше вязкости воды. B. Ее вязкость много меньше вязкости воды. C. Ее вязкость зависит от градиента скорости. D. Ее вязкость не зависит от характера течения жидкости. Е. Только жидкость, не имеющая вязкости может быть ньютоновской. 7. Каким методом определяется вязкость крови? A. Капиллярным и ротационным. B. Методом Стокса. C. Ротационным и методом Стокса. D. Капиллярным и методом Стокса. Е. Капиллярным, ротационным и методом Стокса 8. Кровь является неньютоновской жидкостью, что обусловлено (продолжите фразу)… A. наличием в ней форменных элементов крови B. критическим для крови числом Рейнольдса C. большим коэффициентом вязкости крови D. низким коэффициентом вязкости крови Е. только наличием в крови глобулярных белков 9. При стационарном потоке воды в трубе с переменным сечением в сечении S=100 см  скорость потока равна 75 см/с. Какова скорость течения воды в сечении площадью 20 см скорость потока равна 75 см/с. Какова скорость течения воды в сечении площадью 20 см . .A. 75 см/с B. 18.75 м/с C. 3.75 м/с D. 15 см/с Е. 1.875 м/с 10. Скорость течения воды в широкой части горизонтальной водопроводной трубы равна 50 см/с. Какова скорость течения воды в узкой части той же трубы, диаметр которой в два раза меньше? A. 12.5 см/с B. 25 см/с C. 1.0 м/с D. 2.0 м/с Е. 5 см/с (Эталоны ответов: 1− В; 2− D; 3− D; 4− А; 5− А; 6 − С; 7 − Е; 8 − А; 9 − С; 10 − D) 3) От температуры С увеличением температуры вязкость уменьшается – уменьша- ются силы взаимодействия между молекулами эритроцитов, уменьшаются размеры агрегатов.  Рис. 5.5 В пределах температур от 100С до 380С вязкость крови имеет экспоненциальную зависимость от температуры 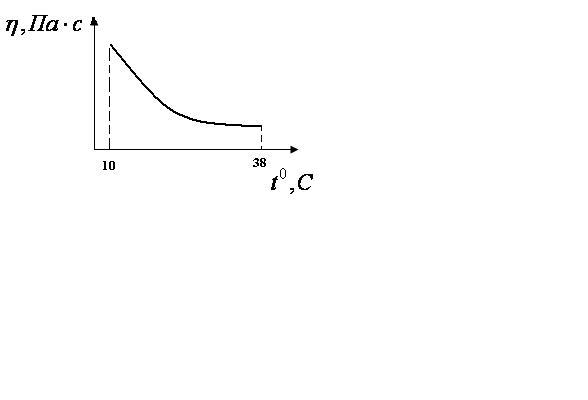 При температурах меньше 100С и выше 380С зависимость очень сложная, что связано с процессами, приводящими к изменению свойств крови. от диаметра сосуда, по которому течет кровь С увеличением диаметра сосуда вязкость крови увеличи-вается. В сосудах диаметром меньше 50 мкм этот эффект проявляется столь сильно, что может маскировать зависимость вязкости крови от скорости сдвига и от гематокритного показателя. 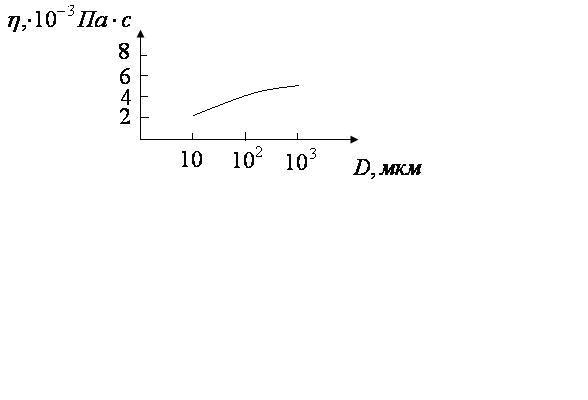 Рис. 5.6 Одно из объяснений этого эффекта такое. В сосудах с боль шим диаметром вся стопка движется целиком, увеличивая вязкость крови. В капиллярах эти агрегаты распадаются, эритроциты могут даже деформироваться - размеры частиц уменьшаются, вязкость падает. 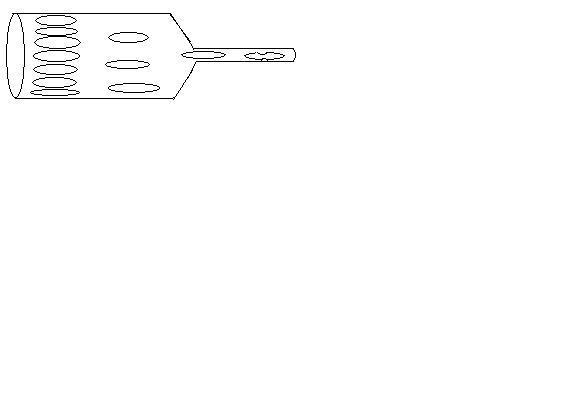 Физические модели кровообращения. Гидродинамическая
Рис. 5.7 Такую модель представляют в виде замкнутой, т.е. не имеющей сообщений с атмосферой системы трубок с эластич-ными стенками. Изначально считаем, что эта система заполнена жидкостью. Движение жидкости в ней происходит под действием ритмично работающего насоса в виде груши. Широкие трубки – аналог аорты и артерий, резкие разветвления – аналог периферической системы – каппиляров. При сжатии груши, содержащийся в ней объём жидкости, проталкивается через отверстие в клапане 1 в систему трубок со стороны трубки А. Затем клапан 1 закрывается. В трубке уже была жидкость под некоторым давлением. Поэтому этот объём жидкости вызывает увеличение давления в широкой трубке, она расширяется. Затем под действием эластичных свойств трубка постепенно сжимается и жидкость проталкивается в следующее звено системы в сторону Б. Когда жидкость подойдет к трубке Б, то через отверстие клапане 2 она попадает снова в насос. Благодаря эластичности стенок трубок и ритмичной работы насоса течение жидкости в системе остается равномерным. В этой системе имеется постепенное и множественное разветвление трубок, особенно в средней её части (множество параллельных трубок малого сечения). Общее число их такое большое, что скорость течения жидкости снижается здесь до нуля. Внутреннее трение в пристеночных слоях этих трубок очень велико, поэтому именно эта часть системы представляет наибольшее сопротивление течению жидкости и создает наибольшее падение давления. Электрическая модель. На основе рассмотренной гидродинамической механической модели можно построить электрическую модель кровообращения.Построена электрическая модель, исходя из следующих соображений. Жидкость течет, ток тоже течет. Перепад давлений вызывает ток жидкости, а разность потенциалов вызывает электрический ток. Н 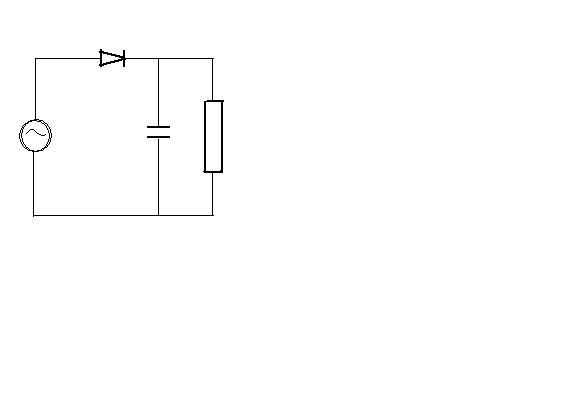 а рисунке: а рисунке:
ра (аорты и артерий). Действительно. Коденсатор служит для накопления заряда. В первые полпериода накапливает заряд, а во вторые полпериода разражается через сопротивление Электрическая модель широко применяется в теоретической медицине, т.к. распределение импульсов электрического потенциала и тока в электрических цепях хорошо изучены и легко описываются математически. 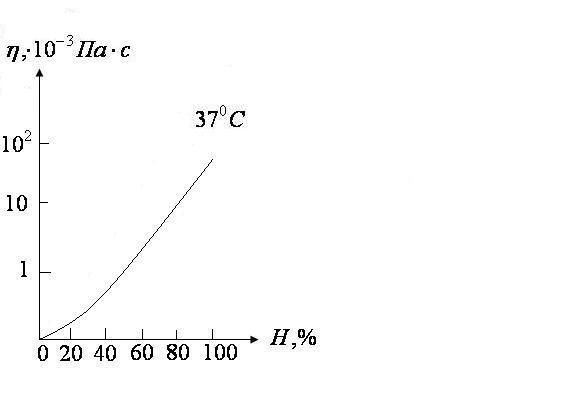 3) От температуры С увеличением температуры вязкость уменьшается – уменьша- ются силы взаимодействия между молекулами эритроцитов, уменьшаются размеры агрегатов.  Рис. 5.5 В пределах температур от 100С до 380С вязкость крови имеет экспоненциальную зависимость от температуры  При температурах меньше 100С и выше 380С зависимость очень сложная, что связано с процессами, приводящими к изменению свойств крови. от диаметра сосуда, по которому течет кровь С увеличением диаметра сосуда вязкость крови увеличи-вается. В сосудах диаметром меньше 50 мкм этот эффект проявляется столь сильно, что может маскировать зависимость вязкости крови от скорости сдвига и от гематокритного показателя.  Рис. 5.6 Одно из объяснений этого эффекта такое. В сосудах с боль шим диаметром вся стопка движется целиком, увеличивая вязкость крови. В капиллярах эти агрегаты распадаются, эритроциты могут даже деформироваться - размеры частиц уменьшаются, вязкость падает.  Физические модели кровообращения. Гидродинамическая
Рис. 5.7 Такую модель представляют в виде замкнутой, т.е. не имеющей сообщений с атмосферой системы трубок с эластич-ными стенками. Изначально считаем, что эта система заполнена жидкостью. Движение жидкости в ней происходит под действием ритмично работающего насоса в виде груши. Широкие трубки – аналог аорты и артерий, резкие разветвления – аналог периферической системы – каппиляров. При сжатии груши, содержащийся в ней объём жидкости, проталкивается через отверстие в клапане 1 в систему трубок со стороны трубки А. Затем клапан 1 закрывается. В трубке уже была жидкость под некоторым давлением. Поэтому этот объём жидкости вызывает увеличение давления в широкой трубке, она расширяется. Затем под действием эластичных свойств трубка постепенно сжимается и жидкость проталкивается в следующее звено системы в сторону Б. Когда жидкость подойдет к трубке Б, то через отверстие клапане 2 она попадает снова в насос. Благодаря эластичности стенок трубок и ритмичной работы насоса течение жидкости в системе остается равномерным. В этой системе имеется постепенное и множественное разветвление трубок, особенно в средней её части (множество параллельных трубок малого сечения). Общее число их такое большое, что скорость течения жидкости снижается здесь до нуля. Внутреннее трение в пристеночных слоях этих трубок очень велико, поэтому именно эта часть системы представляет наибольшее сопротивление течению жидкости и создает наибольшее падение давления. Электрическая модель. На основе рассмотренной гидродинамической механической модели можно построить электрическую модель кровообращения.Построена электрическая модель, исходя из следующих соображений. Жидкость течет, ток тоже течет. Перепад давлений вызывает ток жидкости, а разность потенциалов вызывает электрический ток. Н  а рисунке: а рисунке:
ра (аорты и артерий). Действительно. Коденсатор служит для накопления заряда. В первые полпериода накапливает заряд, а во вторые полпериода разражается через сопротивление Электрическая модель широко применяется в теоретической медицине, т.к. распределение импульсов электрического потенциала и тока в электрических цепях хорошо изучены и легко описываются математически. Закономерности выброса и распространения крови в большом круге кровообращения. Для рассмотрения этого вопроса вернемся к гидродинамической модели кровообращения. Начальное давление, необходимое для продвижения крови по всей сосудистой системе, создается работой сердца. При каждом сокращении левого желудочка сердца в аорту, уже заполненную кровью под соответствующим давлением, выталкиваться некоторый объем крови, называемый ударным объёмом ( Поступивший в аорту дополнительный объём крови повышает в ней давление и растягивает её стенки:  Таким образом, кровь по аорте распространяется как волна. Эта волна повышенного давления, называемого систолическим, вызывает колебания сосудистых стенок. Колебания далее распространяются вдоль крупных артерий в виде упругой волны. Эта волна повышенного давления, вызванная выбросом крови из левого желудочка во время систолы, называется пульсовой волной. Скорость пульсовой волны В период расслабления сердечной мышцы (диастолы) стенки аорты постепенно сокращаются до исходного состояния и проталкивают поступивший объём крови в более крупные артерии. В них, в свою очередь, стенки растягиваются и проталкивают кровь в последующие звенья системы. Т.к. скорость крови Если графически представить пульсовую волну как гармоническую, то в аорте эта волна имеет график вид как на рис. 5.9 а, а в артериолах - как на рис. 5.9 б. 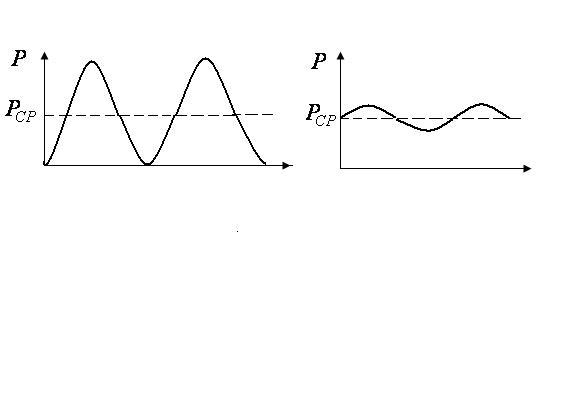
Амплитуда колебаний в аотре больше, чем в артериолах. Вязкость крови и упруго-вязкие свойства стенок сосудов уменьшают амплитуду колебаний пульсовой волны. Течение крови в сосудистой системе в нормальных условиях носит ламинарный характер. Турбулентным оно может стать при резком сужении просвета. Количество крови, протекающее через поперечное сечение участка сосудистой системы в 1 секунду, называется объёмной скоростью кровотока и может быть рассчитана по закону Гагена-Пуазейля Но расчет этот приближенный, т.к. Сопротивление току крови и падение давления на разных участках сосудистой системы различны (рис.5.10) 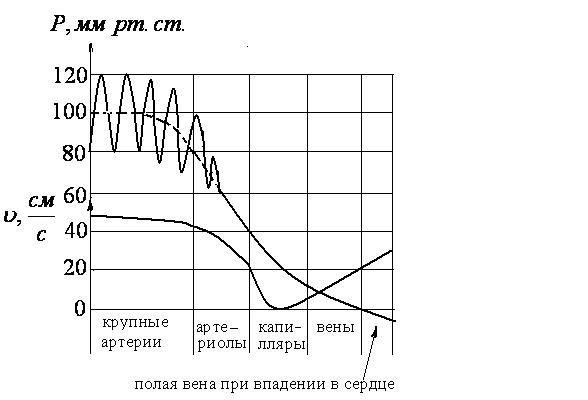 Рис. 5.10 Оно зависит от общего сечения (общего просвета) и от числа сосудов в разветвлении. Наибольшее падение происходит в артериолах (до 50 -ти % от начального). Это связано с тем, что число артериол в сотни раз больше, чем крупных артерий при сравнительно небольшом увеличении общего просвета сосудов. Поэтому потери давления от пристеночного трения достаточно большие. Общее число капилляров ещё больше, поэтому даже при небольшой их длине их падение давления в них значительно, но меньше, чем в артериолах. В венах падение давления незначительно. Это связано с тем, что площадь сечения венозных сосудов в среднем в 2 раза больше, чем в артериях. Имеется участок, в котором давление оказывается ниже атмосферного. Этот участок соответствует движению крови под влиянием присасывающего действия грудной клетки при вдохе. На рисунке представлен также график изменения скорости крови при прохождении её по разным сосудам. Как видим из рисунка в артериях скорость крови постоянна. В артериолах она падает и в капиллярах становится равной нулю. В венах скорость крови повышается. Работа и мощность сердца. Работа, совершаемая сердцем, складывается в основном из работы при сокращении желудочков сердца, главным образом ле-вого желудочка. Работа правого желудочка равна 0,15 –0,2 АЛ.Ж.. Работа сердечной мышцы при каждом сокращении левого желудочка затрачивается на сообщение объёму выталкиваемой крови энергии, необходимой для его продвижения по всему кругу кровеобращения. Эта энергия состоит из потенциальной энергии давления, которое должно быть создано вначале для преодоления по всему её пути, и кинетической энергии для сообщения массе крови необходимой скорости движения: Здесь: При тех условиях, что я здесь привела, получаем за одно сокращение сердца работа левого желудочка: а работа сердца Время сокращения желудочков За одну минуту число сокращений сердца
Основываясь на этих данных, был создан аппарат искусственного кровеобращения. Он представляет собой насосную систему (искусственное сердце) и оксигенератор (искусственные легкие) для обеспечения насыщения крови кислородом. Измерение давления крови. Лабораторный метод измерения давления крови мы уже рассмотрели при изучении вопроса “Следствия из уравнения Бернулли” Бескровный метод измерения артериального давления – метод Короткова, основанный на выслушивании звуков, возникащих при прохождении крови через сжатую манжетой артерию. На предплечье исследуемог укрепляют манжету и прощупывают пульс плечевой артерии несколько выше локтевого сгиба, прикладывают к этому месту фонендоскоп.. Нагнетают в манжету воздух до давления на 10 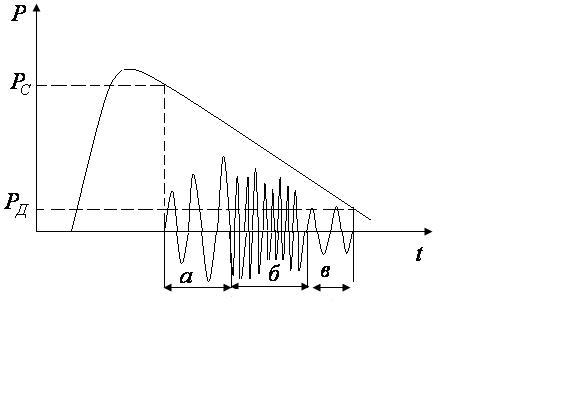 Пока артерия полностью сжата, никаких звуков не прослушивается. При снижении в манжете давления начинают прослушиваться отчетливые тоны, называемые начальными (а на рис.12). Появляется пульс на лучевой артерии. Эти тоны обусловлены вибрацией стенок артерии непосредственно за манжетой под действием толчков крови, которые прорываются через сжатый манжетой участок сосуда только в моменты систолысердца (максимальное давление). Показания манометра при первом появлении тонов соответствуют систолическому давлению. При дальнейшем понижении давления в манжете появляются шумы (б на рис.12) интенсивности больше, чем у тонов. Эти шумы обусловлены турбулентным движением крови через частично сдавленный манжетой участок артерии. Затем шумы стихают и вновь прослушиваются тоны (в на рис.12). Эти тоны быстро стихают и звуковые явления исчезают. Это происходит при полном восстановлении просвета артерии и установлении нормального ламинарного течения крови. Показания манометра в момент резкого ослабления последовательных тонов соответствуют минимальному или даистолическому давлению. В последнее время появились электронные манометры. В них используются параметрические датчики, в которых давление крови меняет какие-либо параметры датчика. В них давление высвечивается прямо на экранчике. |