Вариант 10. Решение Сначала находим по формуле стокса скорость падения пылинок
 Скачать 319 Kb.
|
|
Вариант №10 1. Определите разность фаз в пульсовой волне между двумя точками артерии, расположенными на расстоянии  друг от друга. Скорость пульсовой волны считать равной  , а колебания сердца гармоническим с частотой  Решение Длине волны соответствует разность фаз  , а расстоянию  - разность фаз  , которую следует найти. Составим пропорцию Отсюда ,  , где  .Тогда,  .Ответ: разность фаз в пульсовой волне  .2. Уровень громкости звука частотой 5000 Гц равен  Найти ин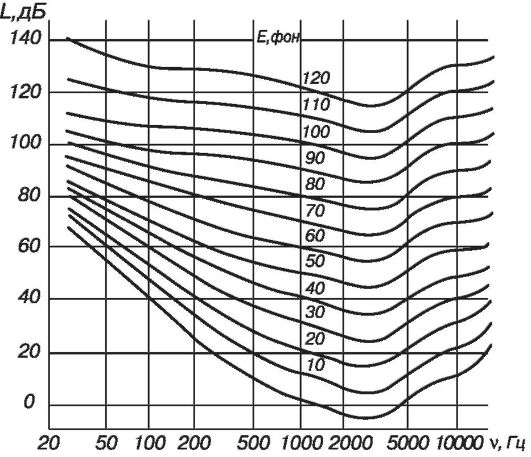тенсивность этого звука, воспользовавшись кривыми равной громкости.Решение:  Рис.1. Кривые равной громкости Из рисунка находим, что на частоте 5000 Гц громкости Е =50 фон соответствует уровень интенсивности L = 47 дБ = 4,7 Б. Из формулы  находим: I = 104,7 I0 = 510-8 Вт/м2.Ответ:I = 510-8 Вт/м2. 3. Используя закон Стокса, определить, в течение какого времени в комнате высотой  полностью выпадает пыль. Частицы пыли считать шарообразными диаметром 1 мкм с плотностью вещества  Решение: Сначала находим по формуле стокса скорость падения пылинок  ,где r – радиус пылинок 1мкм =10-6 м g = 10 м/с2 ρвозд – плотность воздуха в комнате ρпыли – плотность пылинки  м\с.μ – вязкость вещества, в котором находятся пылинки (вязкость воздуха 0,018·10-3) Потом по формуле S=Vt => t=s/v, где s по условию равна 3 м  с.Ответ:  с.4. Кислород массой  , находящийся при нормальных условиях, сжимают до  . Найдите давление  и температуру  кислорода после сжатия и работу А сжатия, если кислород сжимают: а) изотермически; б) адиабатически.
Температура при изотермическом процессе не изменяется  Работа при изотермическом процессе  б) При адиабатическом сжатии (1) Из уравнениния Менделеева-Клапейрона  (2) Давление р2 после сжатия  Температура при адиабатическом сжатии  Давление р2 после сжатия 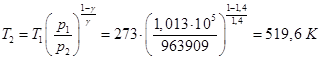 Работа при адиабатическом сжатии 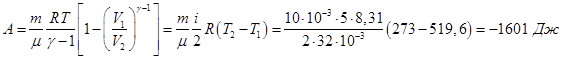 Ответ: а)    б)    5. Рассчитать для равновесного состояния мембранный потенциал создаваемый ионами калия   . Пренебречь проницаемостью ионов натрия и хлора Na+ и С1-..Уравнение Гольдмана – Ходжкина – Катца для мембранного потенциала покоя в стационарном состоянии 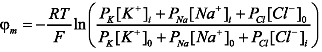 .Пренебрегая проницаемостью ионов натрия и хлора Na+ и С1-, имеем  6. Рамка площадью  содержащая N=10 витков, равномерно вращается с частотой  в однородном магнитном поле с индукцией  . Определите максимальную ЭДС, индуцируемую в рамке, если ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции.Решение:  Рассмотрим один виток рамки. При равномерном вращении его вокруг оси ОО' (рис.) с угловой скоростью ω магнитный поток, пронизывающий площадь, ограниченную этим витком, будет непрерывно изменяться с течением времени по закону Φ = BScosα, где S - площадь рамки; α - угол между нормалью к плоскости и вектором В. Время будем отсчитывать с момента, когда α = 0. Тогда в момент времени t α = wt, следовательно, Φt = BScoswt, а в момент времени t + Δt Ф2 = BScos(w(t + Δt). За промежуток времени Δt магнитный поток изменится на ΔΦ = Ф2 - Φι = BS(cos w(t + Δt) - cos wt) = BS(cos wtcos wΔt - sinwtsinwΔt - coswt). Если Δt очень мало, можно считать cos wΔt = l и sin wΔt = wΔt , поэтому ΔΦ = -BS wΔt sin wt .ЭДС индукции в одном витке  (1) В N витках ЭДС индукции будет в N раз больше, т. е. i = NBSwsinwt, или i = max sinwt, где max - максимальное (амплитудное) значение ЭДС индукции: max = NBSw. (2) Таким образом, при равномерном вращении проводящей рамки в однородном магнитном поле в ней возникает переменная синусоидальная ЭДС индукции. Подставив в выражение (2) значение угловой скорости w = 2π/T, где Т - период вращения рамки  , найдем:  В.Ответ:  В.7. При прохождении монохроматического света через слой вещества толщиной  его интенсивность убывает в 4 раза. Определите показатель рассеяния, если показатель поглощения  .Решение: Запишем формулу ослабления света вследствие поглощения и рассеивания  в логарифмическом виде: 8. В ядро атома азота  попадает  - частица и остается в нем. При этом образуется ядро некоторого элемента и испускается протон. Каков порядковый номер этого элемента в периодической системе элементов?Решение: Запишем уравнение указанной реакции  .Из закона сохранения заряда для этой реакции получим: 7 + 2 = 1+ Z , или Z = 8. 9. Изучение лучевых катаракт на кроликах показало, что под действием 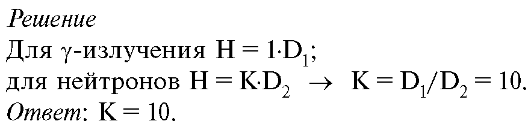 - излучения катаракты развиваются при дозе  . Под действием быстрых нейтронов (залы ускорителей) катаракта возникает при дозе  . Определить коэффициент качества для быстрых нейтронов. Литература Волькенштейн B.C. Сборник задач по общему курсу физики. - М.: Наука,1979. Детлаф А.А., Яворский Б.М. Курс физики. - М.: Высшая школа, 1989. Зисман Г.А., Тодес О.М. Курс общей физики. - М.: Наука, 1974. -Т.1-3. Иродов И.Е. Задачи по общей физике. - М.: Наука, 1987. Медицинская и биологическая физика. Курс лекций с задачами : учеб. пособие / В.Н. Федорова, Е.В. Фаустов. - 2008. - 592 с. Савельев И.В. Курс физики. - М.: Наука, 1989. - Т ..1-3. Трофимова Т.И. Курс физики. - М.: Высшая шкода, 1985. Чертов А.Г., Воробьев А.А. Задачник по физике. - М.: Высшая школа,1988. |
(1) 
