Чураков А. Анализ социальных сетей. А. Н. Чураков анализ социальных сетей
 Скачать 272 Kb.
|
|
СоцИс 2001. № 1. 2000 г. А.Н. ЧУРАКОВ АНАЛИЗ СОЦИАЛЬНЫХ СЕТЕЙ ЧУРАКОВ Александр Николаевич - кандидат социологических наук, старший преподаватель кафедры социологии Московского государственного института международных отношений (Университета) МИД РФ. Анализ социальных сетей (social network analysis) - активно развивающееся направление западной социологии. Интерес исследователей к этому направлению связан с тем, что оно предоставляет новый набор объяснительных моделей и аналитических инструментальных средств, которые находятся вне рамок обычных количественных методов. При этом в данной области накоплен богатый математический аппарат, позволяющий строить весьма сложные модели социальных взаимодействий, описывающие практически любые социальные системы. Сеть социальных взаимодействий состоит из совокупности социальных акторов и набора связей между ними. В качестве социальных акторов могут выступать индивиды, социальные группы, организации, города, страны. Под связями понимаются не только коммуникационные взаимодействия между акторами, но и связи по обмену различными ресурсами и деятельностью, включая конфликтные отношения. Полученная сеть взаимодействий может быть проанализирована различными методами теории графов, теории информации, математической статистики. Анализ социальных сетей используется для исследования и моделирования информационных потоков в сетях, прогнозирования путей развития социальных ситуаций, объяснения специфики исполнения социальных ролей (в том числе и в гендерных исследованиях), анализа процессов социального обмена, изучения структуры социальных организаций и взаимодействий между ними, решения задач социометрии, экономической социологии, социологии массовых коммуникаций и Интернета, истории, политики и международных отношений. Специфика анализа социальных сетей. Весьма часто при проведении исследований классификация объектов по их наблюдаемым характеристикам либо не приводит к содержательному результату (все объекты попадают в одну группу), либо не позволяет выявить причины возникновения в будущем определенной структуры взаимодействий объектов. Анализ социальных сетей позволяет определить различия в сетевом статусе акторов и выявить группы тесно взаимодействующих акторов, что дает возможность находить структурные свойства последних, прогнозировать их поведение, классифицировать акторов по выполняемым ими функциям. В отличие от классических методов анализа, которые исследуют индивидуальные свойства объектов, основные цели анализа социальных сетей – это исследование взаимодействий между социальными объектами (акторами) и выявление условий возникновения этих взаимодействий. Также «сетевой подход исследует образцы связей между индивидами, организациями или институтами для того, чтобы выявить, как социальные структуры возникают на основе взаимодействий субъектов и влияют на эти взаимодействия» [1]. Отсюда следует, что анализ социальных сетей не может быть использован для исследования структуры связей между некоторыми признаками, например, возрастом, расой и профессией, а применяется для анализа структуры взаимодействий социальных субъектов и общностей. Таким образом, анализ социальной сети должен начинаться с изучения социальных взаимодействий акторов и создания схемы этих взаимодействий. Только после этого можно анализировать связь между структурными позициями акторов и их индивидуальными свойствами. В современной западной литературе по социальным сетям в качестве отправной точки данного направления указывается социометрия Дж. Морено. В то же время понятие «сети социальных взаимодействий» встречается еще у Питирима Сорокина. Однако он рассматривал системы взаимодействия как «сложную совокупность координат, определяющих его [индивида - А.Ч.] социальное положение» [2, с. 33], в то время как в анализе социальных сетей исследуется структура взаимодействий индивида с другими индивидами и социальными общностями. Отметим существенное различие между классической социометрией и анализом социальных сетей. В социометрии используются различные индексы отношения к определенному индивиду со стороны других индивидов, как правило, основанные на суммировании числа выборов данного индивида. В то же время известен факт, что для конкретного человека положительная оценка его действий со стороны близкого ему индивида имеет существенно более высокую значимость, чем ряд отрицательных оценок сторонних индивидов. В силу этого социометрические оценки степени социальной изоляции индивида могут искажать реальность, поскольку сам факт отрицательной оценки оказывает влияние на структуру группы. Аналогично индивиды с одинаковым социометрическим статусом могут иметь принципиально различные структуры социальных взаимодействий. Например, отвергаемые группой индивиды могут занять изолированную структурную позицию, отражающую их маргинальный социальный статус. Однако, эта позиция определяется на основе анализа взаимоотношений всех членов социальной группы, а не суммирования положительных и отрицательных выборов данных индивидов. Таким образом маргинал в терминологии теории социальных сетей - это индивид, не взаимодействующий с другими членами группы, в то время как маргинал в социометрии - это индивид, не имеющий положительных выборов, что, однако, не исключает взаимодействия с ним. Направления исследований социальных сетей. В настоящее время в анализе социальных сетей выделяются четыре направления: структурное, ресурсное, нормативное и динамическое [3]. Структурный подход акцентирует внимание на геометрической форме сети и интенсивности взаимодействий (весе ребер). Все акторы рассматриваются как вершины графа, которые влияют на конфигурацию ребер и других акторов сети. Особое внимание уделяется взаимному расположению вершин, центральности, транзитивности (см. ниже) взаимодействий. Для интерпретации результатов в данном случае используются структурные теории и теории сетевого обмена [4-7]. Ресурсный подход рассматривает возможности акторов по привлечению индивидуальных и сетевых ресурсов для достижения определенных целей и дифференцирует акторов, находящихся в идентичных структурных позициях социальной сети, по их ресурсам. В качестве индивидуальных ресурсов могут выступать знания, престиж, богатство, раса, пол. Под сетевыми ресурсами понимаются влияние, статус, информация, капитал [8, 9]. Нормативное направление изучает уровень доверия между акторами, а также нормы, правила и санкции, которые влияют на поведение акторов в социальной сети и процессы их взаимодействий. В этом случае анализируются социальные роли, которые связаны с данным ребром сети, например, отношения руководителя и подчиненного, дружеские или родственные связи. Комбинация индивидуальных и сетевых ресурсов актора с нормами и правилами, действующими в данной социальной сети, образует его «сетевой капитал». В упрощенном виде «сетевой капитал» можно рассматривать как сумму некоторых преимуществ, которые актор может получить в произвольный момент времени для достижения некоторой цели [10-12]. Динамический подход - новое направление в изучении социальных сетей, акцентирующее внимание на изменениях в сетевой структуре с течением времени [13, 14]. Основными исследовательскими вопросами в рамках данного подхода являются следующие: в силу каких причин исчезают и появляются ребра сети? Как сеть изменяет свою структуру при внешних воздействиях? Существуют ли какие-либо стационарные конфигурации социальной сети? Сбор данных. Существуют две различные стратегии сбора данных для анализа социальных сетей. Первая направлена на получение данных о взаимодействиях всех акторов сети, например, всех компаний на рынке информационных систем. В этом случае возникает проблема определения границ сети: если существует сторонний актор, интенсивно взаимодействующий с представителями данной сети, необходимо определить, являются ли эти взаимодействия существенными для структуры сети, и, если это так, то указанный актор должен быть включен в состав анализируемой социальной сети. В то же время ее границы могут задаваться границами исследуемой социальной общности, например, социальная сеть может содержать информацию о взаимодействиях землевладельцев только в пределах данного района страны, при этом их внешние связи не будут рассматриваться. Вторая стратегия может быть названа «актороцентрической» и заключается в сборе данных обо всех взаимодействиях, в которые включен определенный актор. Эта стратегия особенно часто используется при построении социальной сети по результатам опроса респондентов. В этом случае мы можем получить полную информацию о взаимодействиях респондента за определенный промежуток времени и, сравнивая структуры этих взаимодействий, выявить их зависимость от характеристик актора и внешних воздействий. С целью анализа устойчивости и валидности структур получаемых социальных сетей был проведен ряд исследований, направленных на выявление изменения абсолютного размера сети, состава акторов и их рейтингов с течением времени. В результате было установлено, что эти характеристики в среднем устойчивы на 70-95% [15]. Социальные сети могут быть разделены на сети с однотипными и разнотипными акторами. Стандартная и наиболее часто используемая модель социальной сети предполагает идентичность свойств акторов как вершин некоторого графа. В этом случае каждая вершина может быть связана входящими и выходящими ребрами с любыми другими вершинами данного графа, например, вершинами могут быть страны мира, а ребра будут соответствовать торговым отношениям между странами. Социальные сети с разнотипными акторами применяются для анализа структуры некоторых коллективов, например, членства бизнесменов в загородных клубах или борцов за женскую эмансипацию в различных женских организациях. Данная модель может быть использована и для исследования более размытых коллективов, например, посетителей вечеринок или зрителей на спортивных состязаниях. В ней социальная сеть содержит вершины двух типов, соответствующих акторам и коллективам или событиям, и ребра связывают вершины с различными типами. При этом две вершины одного типа не могут быть непосредственно связаны ребром, и путь между ними должен проходить через вершину другого типа. Таким образом, предприниматель, одновременно являющийся членом двух загородных клубов, связывает данные клубы, и клуб, членами которого являются два бизнесмена, связывает этих индивидов [1]. Основные определения. Определим социальную сеть как набор из g социальных акторов и r социальных отношений, показывающих как акторы взаимодействуют друг с другом. Обозначим множество акторов как N={1, 2, ..., g}, а множество социальных отношений как R={1, ... , r}. Определим дихотомическое социальное отношение как множество упорядоченных пар номеров акторов вида (i, j), где на первом месте стоит номер вершины, из которой выходит данное ребро, а на втором месте - номер вершины, в которую входит это ребро. Более наглядно такую пару можно обозначить как ij. Социальное отношение может быть как направленным (независимо друг от друга могут существовать ребра ij и ji), так и ненаправленным (одно ненаправленное ребро соединяет акторов i и j). При этом ребра могут иметь различные веса, показывающие силу взаимодействия. Каждое социальное отношение представляется матрицей связности X размера g g, в которой элемент  В рассматриваемом случае мы имеем r социальных отношений 1,...,r. Обозначим соответствующие им матрицы связности как X1,...,Xr. Можно рассматривать пересечение m n отношений m и n, задаваемое матрицей Xm Xn:  Композиция отношений mn задается матрицей XmXn:  Определим направленный путь длины d из вершины i в вершину j как набор вершин  , такой что  . Самый короткий путь из вершины i в вершину j будем называть дистанцией или расстоянием между этими вершинами и обозначим его длину как  . Величина расстояния не определена, если не существует пути между данными вершинами. Будем называть граф, в котором некоторые расстояния не определены, несвязным графом или графом, состоящим из нескольких компонентов. Для каждого социального отношения рассматриваются большой набор статистик. Укажем лишь наиболее часто используемые из них.
Вводится также ряд статистик, описывающих гомогенные эффекты - число путей длины k; среднее расстояние (близость); минимальное число ребер, удаление которых разбивает граф на несколько частей (связность); и индивидуальные свойства акторов - среднее расстояние от вершины i до остальных вершин; число путей, включающих вершину i (промежуточность). Если акторы разбиты на несколько блоков, то определим индикаторную переменную  Тогда интенсивность взаимодействия блоков r и s:  [1].Основные методы анализа социальных сетей - методы теории графов, в частности, направленные графы и представляющие их матрицы, применяемые для изучения структурных взаимосвязей актора; методы нахождения локальных свойств субъектов, например, центральности, престижа, положения, принадлежности к некоторым подгруппам; методы определения эквивалентности акторов, включая их структурную эквивалентность; блоковые модели и ролевые алгебры; анализ диад и триад; вероятностные модели, включая модели марковских процессов. Далее мы рассмотрим вышеперечисленные методы и приведем примеры содержательных результатов, полученных с их помощью. Графовые модели. Данный класс моделей может быть разделен на три типа:
Для анализа графовых моделей социальных сетей помимо вышеуказанных коэффициентов используется коэффициент плотности - отношение числа ребер в анализируемом графе к числу ребер в полном графе с тем же числом вершин (полный граф - это граф в котором все вершины соединены между собой) [1]. Графовые модели социальных сетей используются для моделирования экономических и коммуникационных связей индивидов, анализа процессов распространения информации, нахождения различных неформальных объединений и связанных подгрупп, на которые можно разбить общую сеть социальных взаимодействий. Например, В. Баскенсом разработана теоретическая модель отношений, основанных на доверии, между продавцами и покупателями на рынке информационных продуктов, учитывающая эффекты управления и обучения. В данной модели различаются два типа взаимодействий: 1) повторяющееся взаимодействие между теми же акторами и 2) общественные сети, которые действуют как информационные каналы и связи между продавцом и покупателем, дающие информацию об отношениях продавца с другими покупателями [11, 12, 16]. Эмпирическая проверка созданной графовой модели проводилась с помощью опроса продавцов и покупателей на рынке информационных продуктов. При этом использовались три меры длины пути в графе: географическое расстояние, плотность графа и информированность покупателя о других продавцах данного продукта. Также учитывалась сложность продукта, его цена и важность для покупателя. В результате был эмпирически подтвержден наблюдаемый на модели эффект, состоящий в том, что чем больше покупателей продуктов у данного продавца знает респондент, тем более сложный контракт он будет заключать с ним, т.е. тем ниже будет уровень доверия респондента к данному продавцу [16]. Анализ центральности и других локальных свойств. Существует несколько подходов для определения центральности акторов. Во-первых, центральные акторы соответствуют тем вершинам сети, которые имеют наибольшее число ребер, т.е. имеют наибольшую степень. Во-вторых, центральная вершина - это вершина, для которой расстояние до остальных вершин сети минимально. В силу этого путь от центральных акторов к другим акторам является наиболее простым, первые имеют большую вероятность получить информацию, циркулирующую в сети, и контролировать распространение этой информации. Третья мера центральности - промежуточность или степень включенности данного актора в маршруты между другими акторами. В этом случае центральным считается актор, который может контролировать наибольшее число путей в социальной сети как между отдельными акторами, так и между их группами [1]. Например, семейство Медичи было актором с наибольшей степенью в сети брачных отношений флорентийской элиты начала XV века. Оно могло контролировать наибольшее количество путей в данном графе. Это позволяет выявить причины, по которым представители этого семейства заняли в дальнейшем доминирующее положение во Флоренции [17]. В то же время, если мы будем рассматривать такие характеристики семей флорентийской элиты, как богатство, древность рода и состояния, политический статус, ближайшее окружение, мы не обнаружим существенных различий между семейством Медичи и остальными олигархами. Этот пример показывает перспективность использования анализа социальных сетей для углубленного понимания социальных процессов и явлений. При анализе реальных социальных взаимодействий часто наблюдается ситуация доминирования одного актора над другим, например, актор А может давать распоряжения актору Б, а Б не может отдавать приказы А, а уполномочен лишь передавать ему некоторую информацию. Моделью этой ситуации будет ориентированный граф с ребрами двух различных типов, соответствующими отношениям иерархии и передачи информации. Ориентированный граф возникает также при анализе известности акторов в сети. В этом случае для определения центральных вершин необходимо рассматривать входную и выходную степень каждой вершины. Акторы с более высоким статусом будут иметь существенно более высокую входную степень по сравнению с выходной, т.е. их будут знать значительно больше акторов, чем они знают сами. Для анализа степени центральности различных акторов используется индекс центральности вершины xi в связном графе G, имеющем одну ось симметрии:  , где  - сумма расстояний от вершины xi до остальных вершин,  - общая сумма дистанций в графе G [18]. Для сравнения графов по степени их центральности вводится индекс центральности графа G: 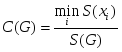 . В [18] доказано, что выполняется условие  , в силу которого C(G) можно нормировать и записать в виде  . Коэффициент (G) = 0 в случае абсолютно не центрального графа (например, замкнутого цикла) и (G) = 1 для центрального графа (звезды).Важными характеристиками сети социальных взаимодействий являются сбалансированность и транзитивность. Сбалансированность - это отсутствие ситуаций типа «позитивное взаимодействие (дружба, партнерство) между А и Б, а также между А и В, но негативное взаимодействие (вражда, соперничество) между Б и В». Утверждается, что сбалансированные сети психологически более комфортабельны для акторов и более устойчивы по сравнению с несбалансированными [19]. Транзитивность - это выполнение условий вида «если есть взаимодействие между А и Б, а также между Б и В, то имеет место взаимодействие между А и В». Данные характеристики описывают локальные связи акторов и часто используются при анализе диад и триад. Сила структурной позиции актора. Основным показателем, который определяет различия в ресурсах акторов, является сила структурной позиции актора. В теории сетевого обмена для измерения данной характеристики вводится индекс силы актора i:  , где  - число непересекающихся путей длины k, проходящих через вершину i. Сила актора i по сравнению с j есть  [3]. Анализ силы структурных позиций является весьма эффективным методом построения моделей, объясняющих различия в результатах деятельности акторов, например, заработной платы работников или прибыли компаний от продажи некоторого товара, особенно в случае малого числа наблюдений. Анализ связанных подгрупп. Связанные подгруппы характеризуются наличием большого числа связей между входящими в них акторами и существенно меньшим числом связей со сторонними акторами. Анализ таких подгрупп позволяет изучать устойчивость социальных структур. Простейший случай связанной группы - это клика или группа акторов, где каждый связан с каждым, и в данную группу не могут быть включены другие акторы, поскольку они не имеют связей со всеми членами клики. Таким образом клика - это максимальный полный подграф данного графа. Если анализировать процессы распространения информации в графах, то можно дать другое определение связанной группы, как множества акторов, где путь между двумя любыми акторами не содержит более одной промежуточной вершины. В результате информация от одного актора к другому в связанной группе передается с минимальными искажениями. Связанные группы также могут быть выделены с помощью многомерного шкалирования или факторного анализа матрицы связей графа. Для анализа устойчивости групповой структуры во времени используется следующая техника. Вначале строится трехмерная матрица, в которой строки представляют оценки взаимодействий данного актора со всеми другими акторами, данные ими; столбцы являются собственными оценками взаимодействий актора; по оси Z располагаются периоды времени. Далее может быть построен график, показывающий изменения структуры подгрупп с течением времени. После этого применяется корреспондентский анализ для описания зависимостей между строками и столбцами данной матрицы. В результате можно визуализировать изменения статуса индивида на фоне изменений статусов подгрупп [19]. Структурная эквивалентность акторов. Этот подход является определенной противоположностью исследованию связанных групп. Акторы эквивалентны, когда они занимают одинаковые позиции в социальной структуре, т.е. когда эквивалентны структура и тип взаимодействий данных акторов с другими, при этом эквивалентные акторы не должны взаимодействовать друг с другом. Например, клиенты продавца некоторого товара будут иметь очень мало или вообще не будут иметь связей между собой (вследствие этого они не будут связанной группой), но все они будут связаны с продавцом, т.е. структура их взаимодействий будет эквивалентна. В качестве меры эквивалентности может выступать плотность связей со структурными подгруппами акторов [1]. Наряду со структурной эквивалентностью используется регулярная эквивалентность акторов. В этом случае акторы эквивалентны, когда они одинаковым образом взаимодействуют с акторами одного типа. Например, двое детей могут быть регулярно эквивалентны, так как они являются лидерами в играх в школьном классе, но они могут принадлежать к разным подгруппам или кликам. Методы определения структурной эквивалентности позволяют анализировать графы с несколькими типами ребер. Например, в случае сети социальных взаимодействий стран мира в качестве этих взаимодействий могут выступать торговля, дипломатические контакты, войны, членство в международных организациях и блоках. Графы, отвечающие каждому типу взаимодействий, могут значительно отличаться, но все вместе они представляют целостную структуру взаимодействий стран мира, из которой можно вывести показатели силы, влияния, уровня развития и экономической мощи данного государства. Для определения структурной эквивалентности двух акторов необходимо сравнить структуру их взаимодействий с другими акторами, т.е. нужно сравнить соответствующие столбцы в матрице связей графа. Это может быть осуществлено с помощью вычисления расстояния между этими векторами (например, по метрике Евклида или Чебышева) или коэффициентов связи (например, корреляции Пирсона). Для направленных графов необходимо учитывать входящие и выходящие ребра, с этой целью одновременно рассматриваются две соответствующие матрицы. Если имеются различные типы взаимодействий между акторами, то строятся матрицы связей графа для каждого типа взаимодействий, а затем эти матрицы составляются по вертикали, т.е. записываются одна под другой. После этого можно сравнивать столбцы полученной матрицы с помощью различных мер расстояния и коэффициентов связи, получая оценку структурной эквивалентности акторов по всему набору их взаимодействий. На следующем этапе в матрицах для каждого типа связей переставляются столбцы таким образом, чтобы сгруппировать те их них, которые соответствуют структурно эквивалентным акторам. В результате матрица разбивается на структурные блоки, в каждом из которых вычисляется плотность. Далее строится новая матрица связей между найденными структурными блоками, например, по следующему правилу: если плотность связей между двумя блоками выше, чем средняя плотность связей в первоначальной матрице, то соответствующий элемент новой матрицы равен 1, в противоположном случае он равен 0. Такие матрицы называются блоковыми моделями и являются средством построения ролевых алгебр. Ролевые алгебры. Это направление анализа социальных сетей фокусируется на выявлении логики взаимодействий акторов в блоковых моделях, что позволяет выявлять сходства принципов взаимоотношений акторов в различных социальных сетях, например, в структурах взаимодействий промышленных рабочих во время Великой Депрессии в США и менеджеров в современной компании, работающей в сфере информационных технологий. Рассмотрим использование ролевых алгебр на вышеуказанном примере взаимоотношений индивидов в трудовом коллективе. Построим матрицы симпатий и антипатий индивидов. Выделим в ней структурные блоки, соответствующие группам симпатизирующих друг другу индивидов. Индивиды из одного блока (клики) симпатизируют друг другу, но испытывают антипатию к индивидам из других блоков. Пусть соответствующие матрицы для простоты имеют вид: СИМПАТИЯ =  , АНТИПАТИЯ =  . После этого мы можем анализировать комбинации взаимодействий, перемножая соответствующие матрицы. Например, умножим матрицу антипатий саму на себя. В результате мы получим матрицу симпатий, что иллюстрирует известное правило «враг моего врага - мой друг». Анализ диад и триад. Диады - это набор из двух акторов (вершин графа) и всех взаимодействий (ребер) между ними. Диада для каждого типа взаимодействий может находиться в одном из четырех состояний: нет связи между акторами, связь направлена от первого актора ко второму, связь направлена от второго актора ко первому, взаимные связи акторов. Анализ диад ориентирован на: 1) установление влияния входной и выходной степени вершин графа на вероятность наличия ребра между ними; 2) выявление обратимости взаимодействия между акторами, степени зависимости от свойств акторов; 3) определение условий и направления передачи информации. Для триад (три взаимодействующих актора) дополнительно исследуются вопросы транзитивности взаимодействий. Важным показателем является сила связей между акторами, которая определяется как линейная комбинация продолжительности, эмоциональной насыщенности, интимности или конфиденциальности и значимости взаимных услуг, которые характеризуют данное взаимодействие и соответствующее ему ребро графа. Слабые связи являются важными источниками информации для актора, так как они служат "мостами" в другие социальные сети, где можно получить дополнительные сведения о некоторой организации или индивиде [4]. Социальные сети могут рассматриваться как источник ресурсов для акторов данной сети. Эти ресурсы включают в себя любые нормативно значимые ресурсы, которые актор может мобилизовать через сетевые связи для достижения желаемого результата. Один из наиболее явных случаев мобилизации сетевых ресурсов мы можем наблюдать, когда контакт с индивидом, обладающим влиянием или занимающим престижную социальную позицию, позволяет родственнику, другу или знакомому найти лучшую и более престижную работу, чем это было бы возможно без использования данного контакта. В то же время актор должен не только иметь возможность мобилизовать сетевые ресурсы, но и быть способным использовать их. Так, если в рассмотренном выше примере влиятельный индивид не связан с возможным работодателем, то сетевой ресурс влияния окажется невостребованным [20]. На основе анализа взаимодействий в диадах разработан ряд теорий, связывающих структуру социальных взаимодействий индивида с вероятностью получения престижной и высокооплачиваемой работы [4, 5, 20, 21]. Эти теории могут быть разделены на две группы, основное различие между которыми состоит в том, что социальные сети могут рассматриваться как источники информации о рабочих местах или источники влияния, необходимого для получения рабочего места. При этом имеет место эффект негативного влияния самостоятельного поиска работы на уровень заработной платы из-за несимметричного потока информации между нанимателем и претендентом на рабочее место. В данном случае наниматель не имеет возможности получить дополнительную информацию о работнике из других источников, кроме него самого, что заставляет подходить с осторожностью к оценке возможностей работника, а, следовательно, и его заработной платы. Если же работника направляет коллега работодателя, то последний может получить от него дополнительную информацию о претенденте. В результате возникает симметричный поток информации, что оказывает положительное влияние на уровень заработной платы работника. Стохастические модели. Основная идея вероятностных моделей направленных графов состоит в том, что каждая социальная сеть может быть рассмотрена как реализация x = {xij} случайного двумерного бинарного массива Х. Так как элементы массива Х являются зависимыми случайными величинами, то можно анализировать структуру зависимостей между соответствующими акторами социальной сети, находить вероятности существования определенных реализаций социальной сети и получать оценки ее параметров. Модели р1. Рассмотрим диаду Dij = ( xij; xji ). Она может находиться в одном из четырех состояний: (0;0) - нулевая диада (нет взаимодействия), (0;1) и (1;0) - асимметричные диады, (1;1) - симметричная (взаимная) диада. Создадим новую матрицу Y размерности gg22 по следующему правилу:  Далее рассмотрим следующую модель:  (1а) (1б)  (1в) (1г) Параметр  описывает склонность субъекта к установлению взаимодействия (его оценкой является выходная степень Dout), параметр  описывает притягательность или популярность (оценка - входная степень Din),  - плотность графа (оценка - число ребер L),  - характеристика тенденций модели к симметричности диад (оценка - число симметричных диад М). В случае ненаправленных взаимодействий имеются только два типа диад и соотношения (1) будут включать только два параметра: оценку интенсивности взаимодействий и .Предположим, что взаимодействия имеют веса в виде целых чисел от 0 до С 1 (С - некоторая константа). В этом случае матрица Y будет иметь размерность ggСС и соотношение (1г) принимает вид:  . Независимо от природы взаимодействий диады предполагаются статистически независимыми и имеющими одинаковое вероятностное распределение, следовательно, можно ввести некоторую функцию правдоподобия, например, произведение вероятностей состояний диад. Поэтому модели типа р1 называют также моделями с независимыми диадами [22]. Модели р*. Определим для дихотомического направленного социального отношения три новые матрицы:  - принудительно добавлено ребро ij,  - принудительно убрано ребро ij,  - все ребра, дополнительные к ij, причем самого этого ребра в матрице нет. Предположим, что вероятность принятия матрицей X значения х равна:  , где ’ - транспонированный вектор параметров модели, z(x) - вектор статистик социальной сети, k - линейная функция, суммирующая произведения элементов вектора и некоторых коэффициентов, и обеспечивающая нужный вид вероятностного распределения. Основная проблема при такой формулировке задачи состоит в определении k, что является весьма сложной задачей для большинства социальных сетей. Однако, можно преобразовать рассматриваемую логлинейную модель в логит-модель, используя то, что случайная величина xij является дихотомической. Отсюда вероятность существования ребра ij: 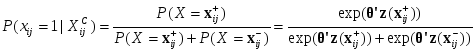 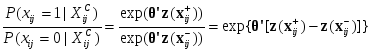 . (2)Если обозначить разность в квадратных скобках как 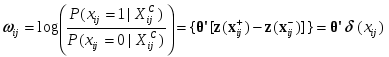 , то логарифм отношения (2) (логит-модель) будет иметь вид:  (3).Элементы - это изменения статистик социальной сети при смене значения xij c 1 на 0. Такой вариант модели, в которой логарифм отношения вероятностей равен линейной комбинации элементов , называется логит-моделью р* для единичного дихотомического социального отношения. Для случая ребер с весами от 0 до С 1 мы будем иметь набор из С-1 логит-моделей [23]. Статистическая интерпретация логистических регрессионных моделей для  зависит от предположения о независимости величин . В модели р* логит-модели для не являются независимыми, в силу чего статистика отношения правдоподобия не поддается строгой статистической интерпретации, хотя ее значение может служить ориентиром качества построенной модели.Графы зависимости. На базе социальной сети можно построить граф зависимости D, показывающий, какие ребра или группы ребер условно зависимы. Два ребра называются условно зависимыми, если условная вероятность одновременного существования этих ребер, вычисляемая по остальным ребрам сети, не равна произведению условных вероятностей независимого существования этих ребер. Граф зависимости имеет ребра, связывающие все пары условно зависимых ребер социальной сети. Обозначим множество вершин графа зависимости как ND={(i, j, m); i, jN, i j; mR} (мы рассматриваем граф зависимости для случая нескольких типов взаимодействий). С помощью теоремы Хаммерсли-Клиффорда можно формально установить, как структура социальной сети влияет на параметры модели р*. Данная теорема утверждает, что вероятность существования случайного направленного графа зависит только от полных подграфов в графе зависимости и может быть представлена в виде:  , гдеD - граф зависимости для Х,  - нормирующая константа,суммирование идет по всем подмножествам А множества ND,  - достаточные статистики, соответствующие параметру  , причем в случае, когда подграф, задаваемый вершинами, входящими в А, не является полным [24].Ненулевые параметры модели соответствуют набору максимальных полных подграфов (клик) графа зависимости. Напомним, что полным подграфом называется такой набор вершин, где каждая их пара связана ребром, т.е. полный подграф в графе зависимости соответствует набору ребер социальной сети, каждая пара которых является условно зависимой. Максимальный полный подграф - это полный подграф, который не полностью содержится в любом другом полном подграфе. Так как каждый подграф полного подграфа также является полным, следовательно, если А - это максимальная клика D, то ненулевые параметры модели будут при А и всех его подграфах. Использование теоремы Хаммерсли-Клиффорда позволяет существенно упростить процесс построения моделей р*. Например, логлинейная модель Марковского графа зависит только от полного набора триад и звезд размера k, но не от тетрад и других полных подграфов. При этом модель можно дополнительно упростить с помощью предположений о гомогенности ее параметров, т.е. их независимости от индивидуальных акторов. Оценка параметров модели р*. Функция правдоподобия для модели р* может быть записана в виде  . В этом случае опять возникает проблема определения функции k. Избежать этого можно при использовании так называемой функции псевдоправдоподобия, получаемой при допущении условной независимости ребер и переходе к логит-модели, и имеющей вид:  (4). Оценка максимального псевдоправдоподобия отвечает максимальному значению выражения (4). Отметим, что оценка максимального правдоподобия не отличается от оценки максимального псевдоправдоподобия только на классе простейших графовых моделей, у которых условные вероятности существования ребер не зависят от структуры ребер данного взаимодействия, т.е. в случае условной независимости ребер. Д. Страуссом и М. Айкедой доказана теорема о том, что в случае логит-модели р* в форме (3) максимизация значения функции псевдоправдоподобия (4) эквивалентна максимизация функции правдоподобия для логистической регрессии в модели (3) для независимых наблюдений {xij}. Такая аппроксимация может быть выполнена с помощью итеративного метода Гаусса-Ньютона с перевзвешиванием [23, 24]. Обозначим оценки параметров модели, полученные с помощью логистической регрессии, как  . Оценивать качество аппроксимации будем с помощью статистики  . Для проверки статистической значимости каждой характеристики сети, например, взаимности, рассматриваются две модели, содержащая данную характеристику, и не содержащая ее. Значимость различий в значениях статистики  для этих моделей может быть приближенно оценено с помощью распределения  с числом степеней свободы, равным числу параметров модели, связанным с этой характеристикой. Также значимость коэффициентов регрессии можно проверить с помощью статистики Вальда, используя их приближенную стандартную ошибку. В заключение предпримем попытку перечислить наиболее актуальные и важные в настоящее время проблемы анализа социальных сетей, решение которых позволит существенно расширить как объяснительные возможности, так и сферу применения данного научного направления.
СПИСОК ЛИТЕРАТУРЫ
|
.
.
.
. 
.
.