Теория графов. А (Рис. 1 не изоморфен ни одному из остальных) Граф

• Название: А (Рис. 1 не изоморфен ни одному из остальных) Граф
• Анкор: Теория графов
• Дата: 06.11.2021
• Размер: 265.56 Kb.
• Имя файла: Теория графов.docx
• Тип: Документы; #264726

1. 
   Определить, какой из графов (если такой есть) не изоморфен ни одному из остальных (в ответ указать букву списка для соответствующего графа). Для остальных графов определить, какому (каким) из графов они изоморфны.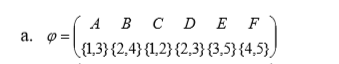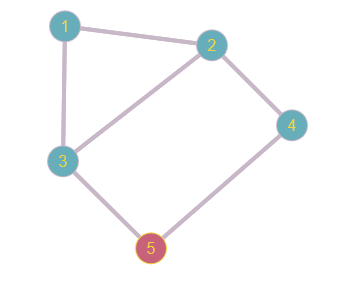
   

Рис.1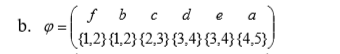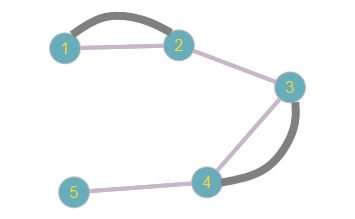





Рис.2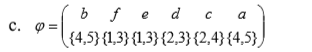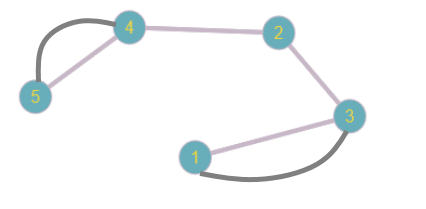





Рис.3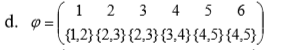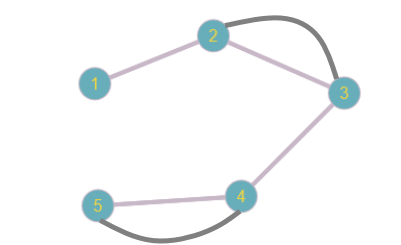





Рис.4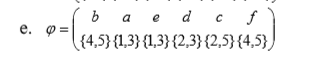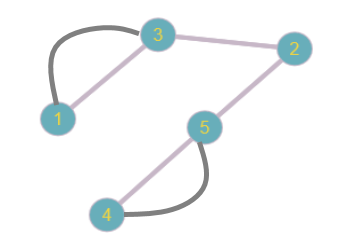





Рис.5

Ответ: а (Рис.1 не изоморфен ни одному из остальных)

Граф e изоморфен графу с ( рис.3 и рис.5)

Граф b изоморфен графу d ( рис.2 и рис.4)

Граф b изоморфен графу c( рис.2 и рис.3)

Граф b изоморфен графу e( рис.2 и рис.5)

Граф c изоморфен графу d( рис.3 и рис.4)

2. 
   Самостоятельно подготовить задание, аналогичное задаче 1 (пять графов по 6 вершин). Для иллюстрации использовать одно из online средств визуализации графов. При оформлении решения этой задачи указать список графов, записанных в текстовой форме в виде перечисления ребер; скриншоты графов; ответ (буква списка выбранного графа (неизоморфного другим)); ответ по изоморфности остальных графов (например, ― граф a) изоморфен графу e) ‖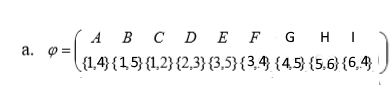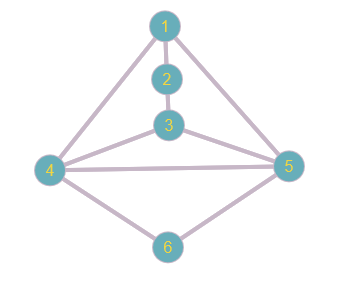
   

Рис.7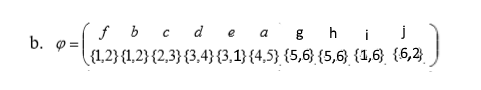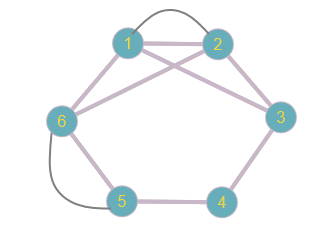





Рис.8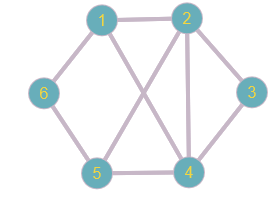





Рис.9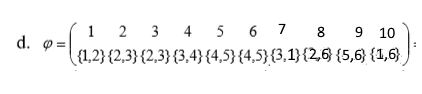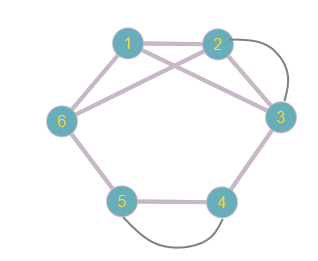





Рис.10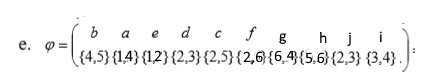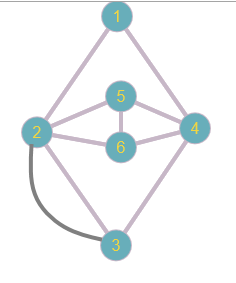





Рис.11

e (Рис.11 не изоморфен ни одному из остальных)

Граф а изоморфен графу c( рис.7 и рис.9)

Графb изоморфен графу d( рис.8 и рис.10)

3. 
   Покажите, что следующие графы являются изоморфными (аналогично приведенному выше примеру):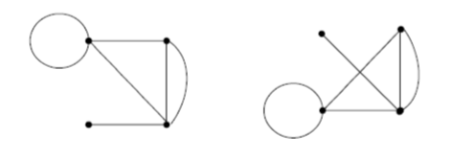
   

Рис.12

Проверим выполнение необходимых условий:

1. число вершин у графов одинаковое;

2. число ребер одинаковое;

3. параллельные ребра в обоих графах присутствуют;

4. петли в обоих графах есть;

5. степени вершин совпадают

6. оба графа связные;

7. в обоих графах циклы есть.

Таким образом, получается, что возможно графы являются изоморфными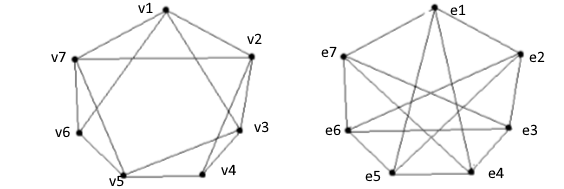



Рис.13

Проверим выполнение необходимых условий:

1. число вершин у графов одинаковое;

2. число ребер одинаковое;

3. параллельные ребра в обоих графах отсутствуют;

4. петли в обоих графах отсутствуют;

5. степени вершин совпадают по 7 вершин со степенью 4;

6. оба графа связные;

7. в обоих графах циклы отсутствуют.

Оба графа изоморфны, так как существует взаимно однозначное соответствие 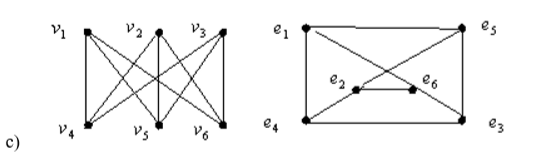, сохраняющее смежность. Говорят, что граф  изоморфно вкладывается в граф , если  изоморфен некоторой части графа .



Рис.14

Проверим выполнение необходимых условий:

1. число вершин у графов одинаковое;

2. число ребер одинаковое;

3. параллельные ребра в обоих графах отсутствуют;

4. петель в обоих графах нет;

5. степени вершин совпадают

6. оба графа связные;

7. в обоих графах циклы отсутствуют.

Оба графа изоморфны, так как существует взаимно однозначное соответствие , сохраняющее смежность. Говорят, что граф  изоморфно вкладывается в граф , если  изоморфен некоторой части графа .