4809872 вар 7. Решение. Событие а на обеих костях появилось одинаковое число очков. Используем классическое определение вероятности
 Скачать 291.5 Kb. Скачать 291.5 Kb.
|
|
1. Брошены две игральные кости. Найти вероятность того, что на обеих костях появится одинаковое число очков. Решение. Событие А – на обеих костях появилось одинаковое число очков. Используем классическое определение вероятности Всего при бросании двух кубиков возможно Найдем число благоприятных исходов: 1-1, 2-2, 3-3, 4-4, 5-5, 6-6, т.е. Тогда получим: 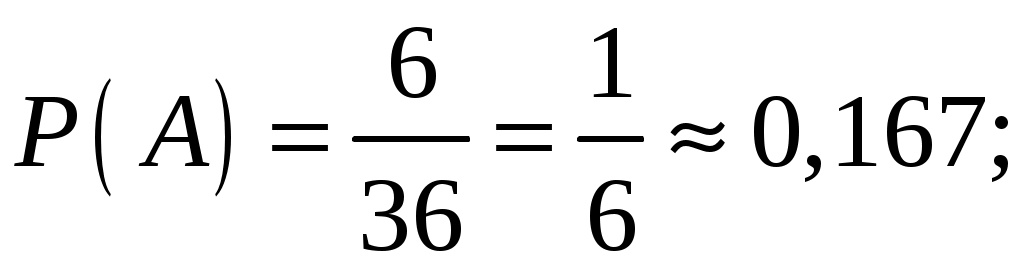 Ответ: 2. Вероятность того, что некоторое изделие имеется в первом магазине 0,5; во втором – 0,7; в третьем – 0,4. Какова вероятность, что изделие найдется: а. хотя бы в одном магазине; б. только в одном магазине. Решение. Пусть событие тогда По условию, вероятности того, что изделие найдется в 1-ом, 2-ом и 3-ем магазине соответственно, равны: Тогда вероятности того, что в 1-ом, 2-ом и 3-ем магазине соответственно изделия нет, равна: а. Событие А – изделие найдется хотя бы в одном магазине. Так как наличие изделия в одном магазине не зависит от его наличия в другом магазине, т.е. Тогда искомая вероятность равна: б. Событие В – изделие найдется только в одном магазине. Используя предыдущие обозначения получим: Так как наличие изделия в одном магазине не зависит от его наличия в другом магазине, т.е.  Ответ: а. 0,91; б. 0,36. 3. У сборщика имеется 20 деталей: 10 – I сорта, 6 - II сорта, 4 - III сорта. Наудачу взяты 3 детали. Найти вероятность, что все они III сорта. Решение. Событие А – все взятые детали III сорта. По классическому определению вероятности, где Используя формулу сочетаний 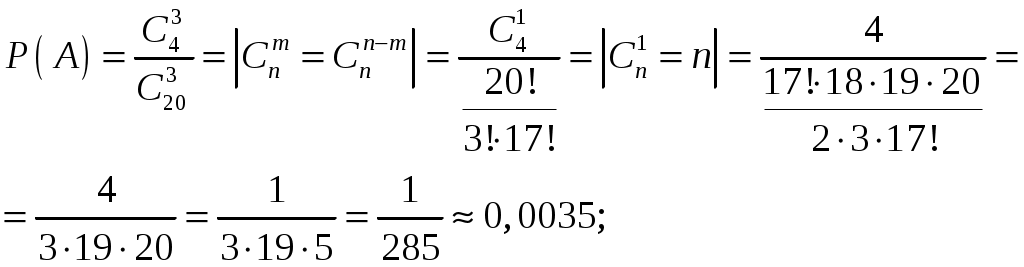 Ответ: 4. Вероятность изготовления детали отличного качества равна 0,9. Какова вероятность того, что среди 10 деталей 9 отличного качества. Решение. Событие А – среди взятых наугад 10 деталей 9 отличного качества. Так как число деталей невелико, то используем формулу Бернулли: По условию, число деталей 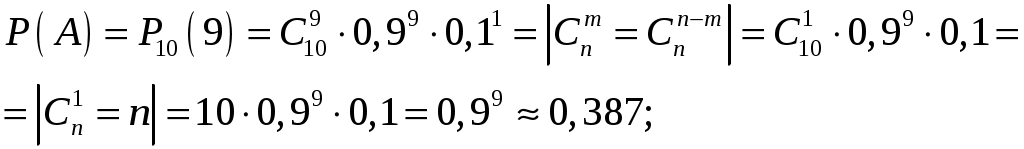 Ответ: 0,387. 5. Составить закон распределения случайной величины Решение. Случайная величина Вычислим значения этой случайной величины, используя формулу Бернулли: Вероятность попадания при одном броске 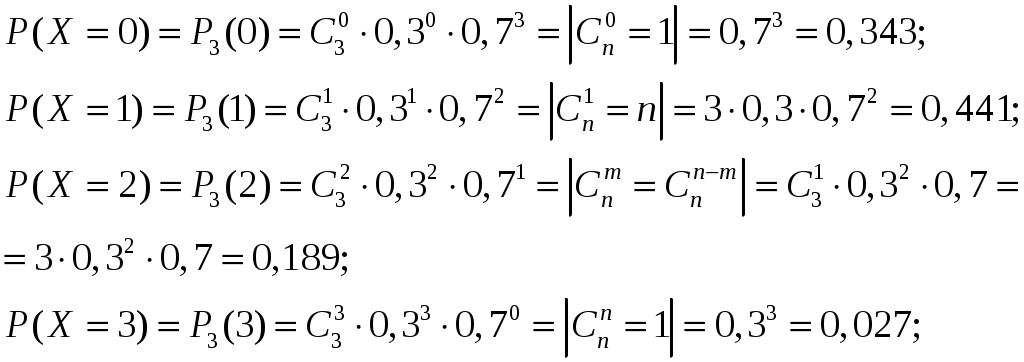 Тогда закон распределения имеет вид:
Контроль:  . .Распределение, при котором значения СВ Математическое ожидание биномиального распределения находится по формуле: Дисперсия биномиального распределения находится по формуле: Среднее квадратическое отклонение: 4) Найдем интегральную функцию распределения: Если Если Если Если Если Таким образом, функция распределения имеет вид: 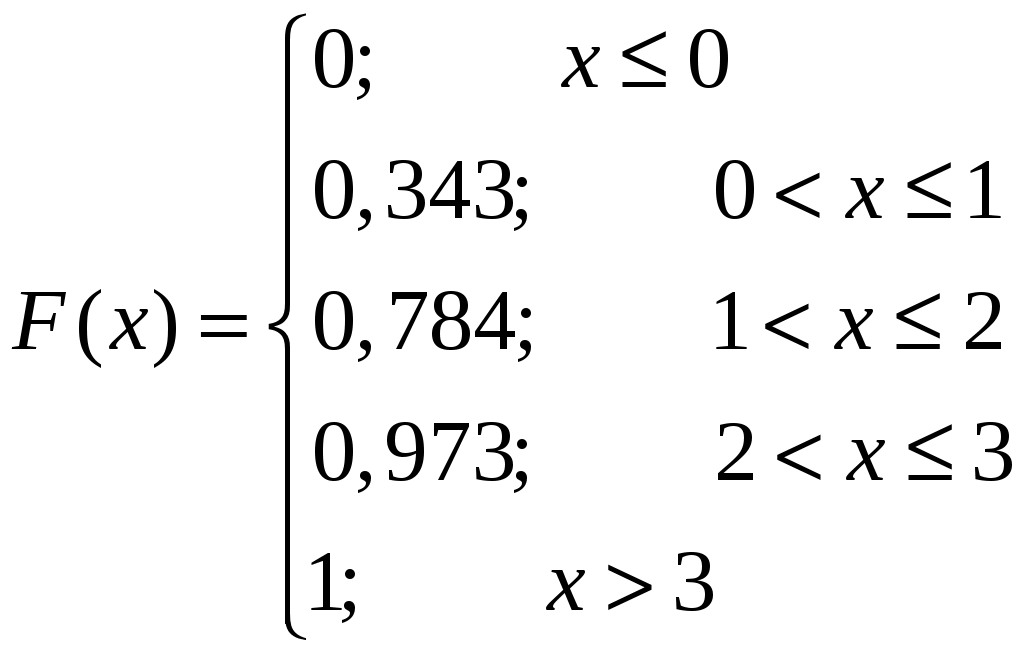 График функции распределения имеет вид: 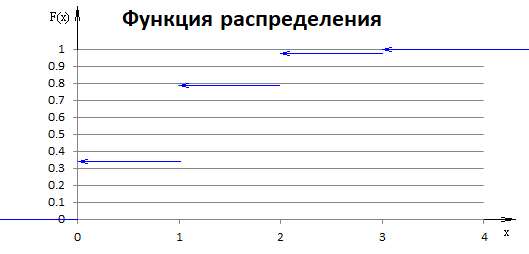 6. Деталь, изготовленная автоматом, считается годной, если отклонение ее контролируемого размера от проектного не превышает 10 мм. Случайные отклонения контролируемого размера от проектного подчиняются нормальному закону с Решение. Вероятность того, что абсолютная величина отклонения значений нормально распределенной случайной величины от ее математического ожидания не превысит 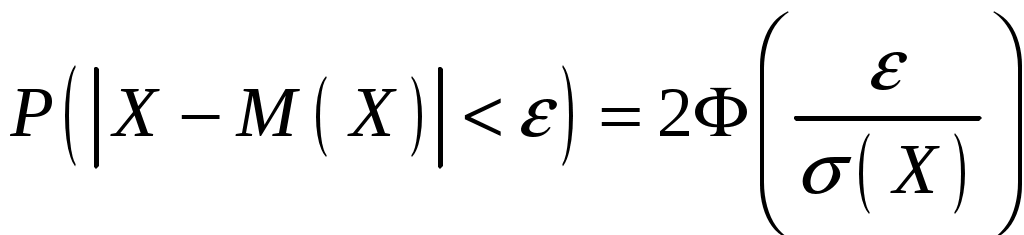 . .По условию, тогда Подставляя данные значения в формулу, получим: 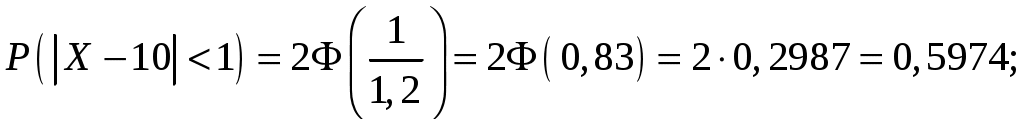 Т.е. автомат изготавливает Ответ: 59,74%. 7. На склад магазина поступают изделия, из которых 80% высшего сорта. Найти вероятность того, что из 100 наудачу взятых изделий не менее 65 высшего сорта. Решение. Событие А – из 100 наудачу взятых изделий не менее 65 высшего сорта. Так как число изделий велико, то используем интегральную теорему Лапласа: По условию, число изделий 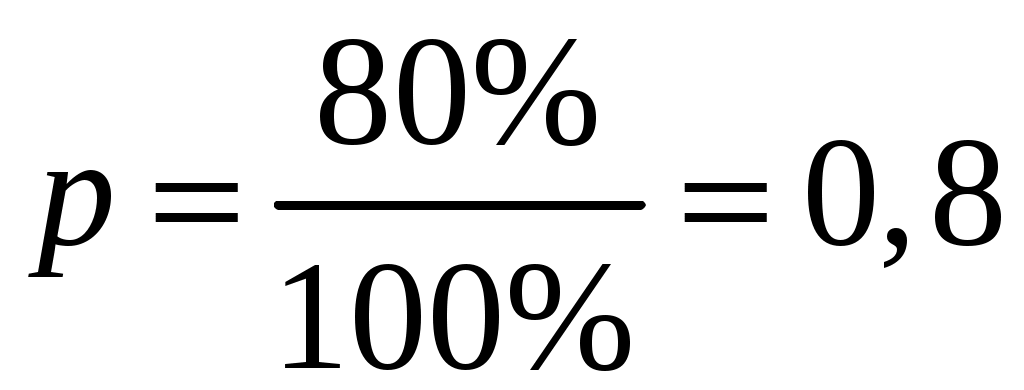 , , тогда Подставив найденные значения и 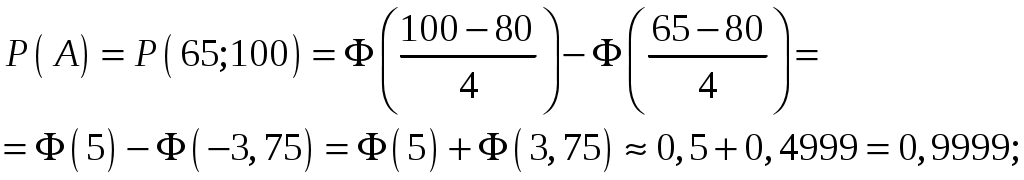 Ответ: 0,9999. 8. По данной выборке найти несмещенные оценки средней генеральной, генеральной дисперсии и генерального среднего квадратического отклонения. Найти доверительный интервал для средней генеральной с указанной доверительной вероятностью
Решение. Найдем объем выборки:  . .Для вычисления средней выборочной и дисперсии составим таблицу.
Найдем выборочную среднюю: 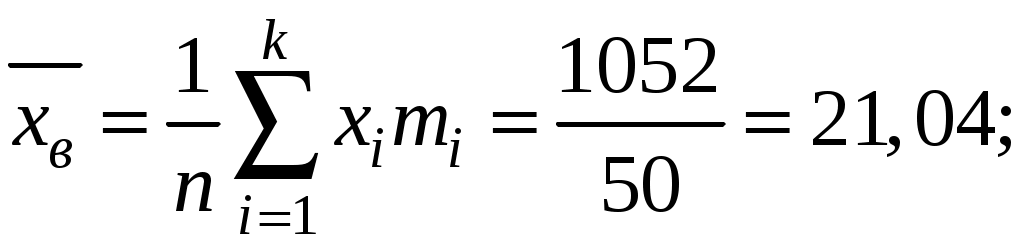 Найдем выборочную дисперсию: 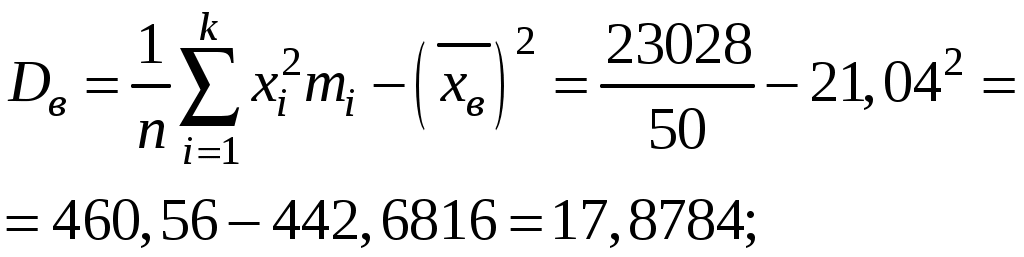 Точечная несмещенная оценка средней генеральной - выборочная средняя: Точечная оценка генеральной дисперсии – исправленное среднее квадратическое отклонение:  Точечная оценка генерального среднего квадратического отклонения – исправленное среднее квадратическое отклонение: Найдем доверительный интервал для средней генеральной с доверительной вероятностью При известном генеральном среднем квадратическом отклонении (СКО) доверительный интервал для оценки средней генеральной (математического ожидания) при заданной надежности находится с помощью функции Лапласа и имеет вид: Ранее вычислены выборочное среднее Все параметры, кроме Построим доверительный интервал с помощью коэффициента Стьюдента. Найдем  . . Тогда 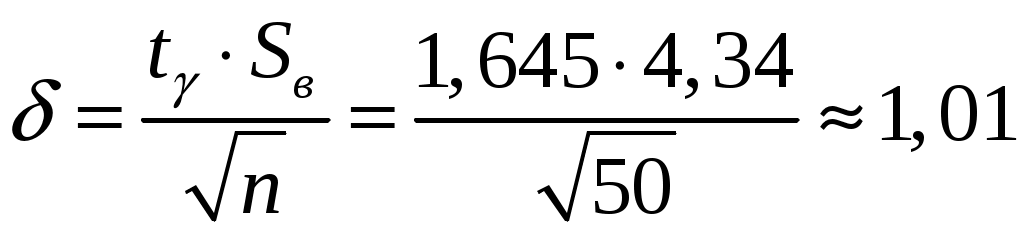 , ,откуда получим: |
