контрольная. A справедливо ли в общем случае утверждение если
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
A) Справедливо ли в общем случае утверждение: если 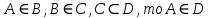 ? ?Пусть  , тогда по определению , тогда по определению , поэтому данное утверждение верно. , поэтому данное утверждение верно.Б) Может ли при некоторых А, В, С и D выполниться набор условий: 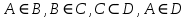 : Да, может, что следует из справедливости утверждения в п.А : Да, может, что следует из справедливости утверждения в п.А1.1.2) Для универсального множества 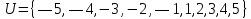 , множества А, заданного списком , множества А, заданного списком 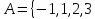 } и для В, являющимся множеством корней уравнения } и для В, являющимся множеством корней уравнения   Решим уравнение. Подбором находим корень x=-1, делим многочлен на (x+1) дважды, т.к. корень подходит два раза. Получаем уравнение 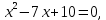 по теореме Виета два корня x=2, x=5. по теореме Виета два корня x=2, x=5. 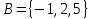 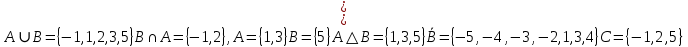 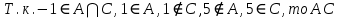 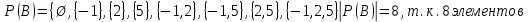 1.1.3) Пусть А, В и С - множества точек плоскости, координаты которых удовлетворяют условиям  соответственно. Изобразите в системе координат хОу множество D , полученное из множеств А, В и С по формуле соответственно. Изобразите в системе координат хОу множество D , полученное из множеств А, В и С по формуле  . . 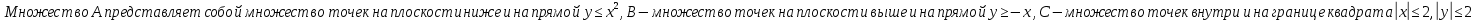 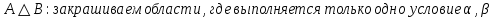         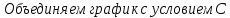 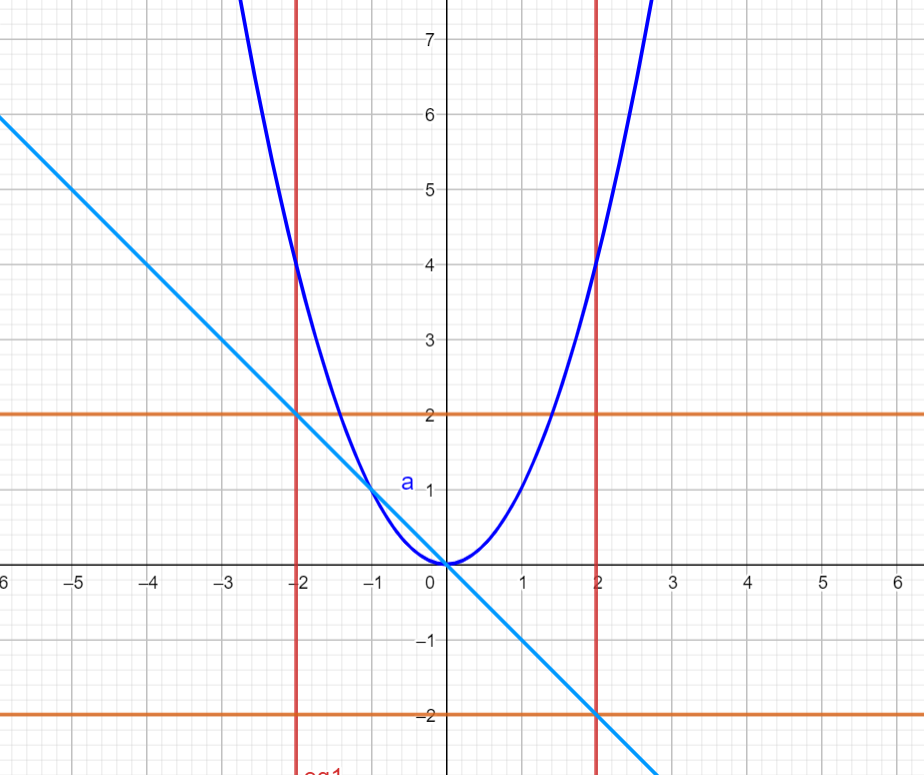           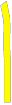  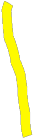    1.1.4) 1. Существуют ли множества А, В, X такие, что выполняется набор условий 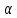 ? 2. Существуют ли множества N, Е, Р такие, что выполняется набор условий ? 2. Существуют ли множества N, Е, Р такие, что выполняется набор условий 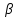 ? ?  1. Изобразим множества А, В, X в виде прямоугольников, расположенных на плоскости в общем положении, и поставим в каждой области, на которые плоскость разбита прямоугольниками, по одному символу: Символ 4, например, обозначает список всех элементов, попавших во множества А и В, но не попавших в X , и т.д. Теперь составим множества А, В, X и универсальное множество U : U = { 1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 } , А = {1 ,2 ,4 ,5 }, В = {4 ,5 ,6 ,7}, Х = { 2 ,3 ,5 ,7}. Изменим множества А, В, X так, чтобы выполнились условия нашего задания. 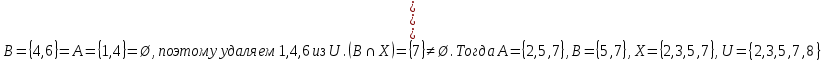 . Если под символами 2, 3, 5,7,8 будем понимать соответствующие числа, то мы получим конкретный пример множеств А, В, X , для которых выполнены все условия заданного набора требований. . Если под символами 2, 3, 5,7,8 будем понимать соответствующие числа, то мы получим конкретный пример множеств А, В, X , для которых выполнены все условия заданного набора требований. 2. Попробуем построить множества N , Е, Р так же, как мы это делали в п.1. Пусть N ={1 ,2 ,4 ,5 }, Е ={4 ,5 ,6,7}, Р ={2 ,3 ,5 ,7}. 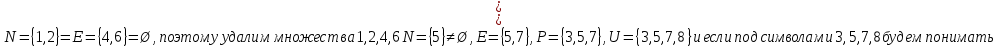   Существуют 1.1.5) Выяснить взаимное расположение множеств D, Е, F, если А, В, X - произвольные подмножества универсального множества U.  Возьмём множества А, В, X , находящиеся в общем положении: А = {1,2,4,5}, В = {4,5,6,7}, X = {2,3,5,7}. В нашем случае, как и при решении задания 1.1.3, цифры обозначают соответствующие списки переменных.  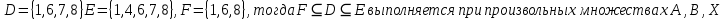 1.1.8) Решить систему соотношений относительно множества X и указать условия совместности системы 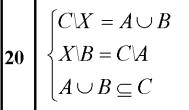 Построим таблицу возможных наборов
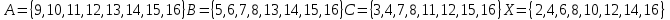 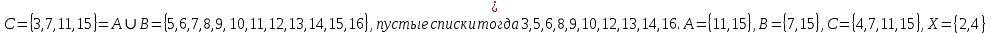 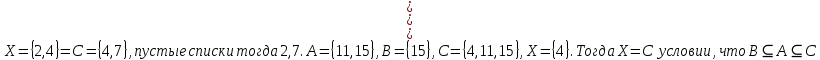  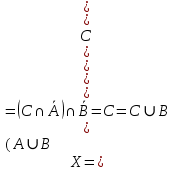 1.2.1) 1. Проверить справедливость равенства а для множеств А — {1,2}, В = {2,3}, С = {1,3}. 2. Выяснить, верно ли равенство а для произвольных А, В, С. 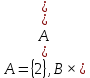    1.2.2) 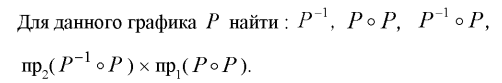   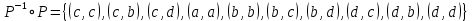  1 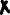 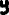 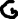  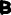 .3.1) Дано соответствие Г = (X,Y,G). 2. Выяснить, какими из 4 основных свойств (всюду определённость, сюръективность, функциональность, инъективность) обладает Г. 3. Найти образ множества А и прообраз множества В при данном соответствии. .3.1) Дано соответствие Г = (X,Y,G). 2. Выяснить, какими из 4 основных свойств (всюду определённость, сюръективность, функциональность, инъективность) обладает Г. 3. Найти образ множества А и прообраз множества В при данном соответствии. Соответствие не всюду определено, так как  Соответствие сюръективно, так как 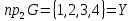 Соответствие не функционально, так как его график содержит две пары (a,1), (a,2) с одинаковыми первыми и различными вторыми координатами Соответствие инъективно, так как его график G не содержит пар с одинаковыми вторыми и различными первыми координатами. Найдём образ Г (А) и прообраз Г-1(В).   1.4.1)  Для антирефлексивных отношений 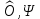 выполнены условия: выполнены условия:   2.1.1) Построить таблицу данной булевой функции f (х, у, z)
2.1.2) 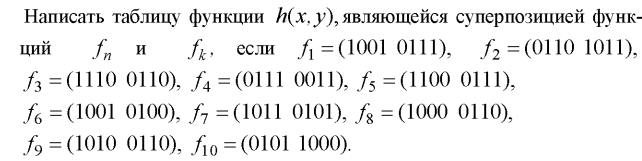   Сначала запишем таблицу функций
Составим таблицу функции h(x, у). Для этого запишем формулу, задающую функцию h(x, у), выпишем под символами переменных все наборы значений, которые эти переменные принимают, а под символами булевых функций будем выписывать значения функций, соответствующие этим наборам. Заключительный столбец, задающий функцию h,выделим. H(x, y)= f10 (x, f9( x x y), y)
h(x,y)=(0100) 2.1.3) Для данной функции f (х, у, z) 1. Выяснить, какие её переменные являются существенными, а какие - фиктивными. 2. Выразить f(x,y,z) формулой, содержащей только существенные переменные.f=
Переменная х является фиктивной для данной бф, так как на всех наборах, соседних по переменной x, значения функции равны, то есть выполняются равенства: f(0,0,0)=f(1,0,0)=0, f(0,0,1)=f(1,0,1)=1, f(0,1,0)=f(1,1,0)=1, f(0,1,1)=f(1,1,1)=1 Переменная y является существенной для данной бф, так как, например, наборы (0,0,0) и (0,1,0) являются соседними по переменной y и f ( 0 ,0 ,0 )  (0,1,0). (0,1,0).Переменная z является существенной для данной бф, так как, например, наборы (0,0,0) и (0,0,1) являются соседними по переменной z и f ( 0 ,0 ,0 )  (0,0,1). (0,0,1).Выпишем таблицу функции f, как функцию только от существенных переменных
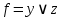 2.1.4) 1. Написать таблицу булевой функции f (х, у, z), заданной формулой. 2. Найти фиктивные переменные данной функции. 3. Преобразовать данную формулу в эквивалентную ей, но не содержащую фиктивных переменных. F=
Переменная х является фиктивной для данной бф, так как на всех наборах, соседних по переменной x, значения функции равны, то есть выполняются равенства: f(0,0,0)=f(1,0,0)=0, f(0,0,1)=f(1,0,1)=1, f(0,1,0)=f(1,1,0)=1, f(0,1,1)=f(1,1,1)=1 Переменная y является существенной для данной бф, так как, например, наборы (0,0,0) и (0,1,0) являются соседними по переменной y и f ( 0 ,0 ,0 ) 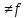 (0,1,0). (0,1,0).Переменная z является существенной для данной бф, так как, например, наборы (0,0,0) и (0,0,1) являются соседними по переменной z и f ( 0 ,0 ,0 ) 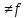 (0,0,1). (0,0,1).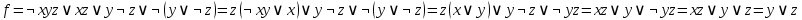 2.2.1) Выяснить взаимное расположение множеств D, Е, F, если А, В, С - произвольные подмножества универсального множества U.  Найдём соответствующие булевы функции: 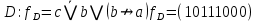  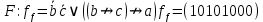 Так как множество единичных наборов функций 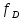 и и строго включены в множество единичных наборов функции строго включены в множество единичных наборов функции  , то , то   2.2.3) Для произвольных множеств А, В, Н проверить, является ли выполнение включения 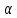 необходимым и достаточным условием выполнения равенства необходимым и достаточным условием выполнения равенства 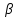 Составим булеву функцию, соответствующую высказыванию, которое надо доказать: 
Построим таблицу, убедимся, что заключительный столбец, являющийся вектором значений функции f ( a ,b ,h ) состоит из одних единиц, что доказывает справедливость требуемого утверждения. 2.3.2) 1. Выяснить вопрос о равносильности ДНФ 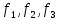 сведением их к СДНФ. 2. Преобразовать с помощью дистрибутивных законов сведением их к СДНФ. 2. Преобразовать с помощью дистрибутивных законов 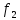 в КНФ, упростить полученное выражение. в КНФ, упростить полученное выражение.   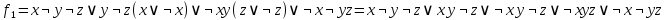  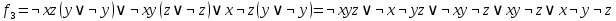 Сравнивая СДНФ этих функций, делаем вывод, что  2. Преобразуем 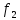 в КНФ. Воспользуемся одним из дистрибутивных законов: в КНФ. Воспользуемся одним из дистрибутивных законов: 2.3.3) 1. Найти двумя способами полином функции, заданной векторно. 2. Найти СДНФ; 3. СКНФ данной функции. F= Запишем таблицу данной функции в развёрнутом виде:
Способ 1. Применим метод неопределённых коэффициентов. Будем искать полином для данной функции в виде: f(х, у, z) = a000 ⊕ a001x ⊕ а010у ⊕ a011z ⊕ а100ху ⊕ a101xz ⊕ a110yz ⊕ a111xyz. Используя таблицу функции, будем подставлять наборы значений переменных и значения функции в это соотношение и последовательно находить неопределённые коэффициенты аi: f(0,0,0) = a000 = 0 ⇒ a000 = 0 f(1,0,0) = a000 ⊕ a100 = 0 ⊕ a100 = 1 ⇒ a100 = 1 f(0,1,0) = a000 ⊕ a010 = 0 ⊕ a010 = 0 ⇒ a010 = 0 f(0,0,1) = a000 ⊕ a001 = 0 ⊕ a001 = 1 ⇒ a001 = 1 f(1,1,0) = a000 ⊕ a100 ⊕ a010 ⊕ a110 = 0 ⊕ 1 ⊕ 0 ⊕ a110 = 0 ⇒ a110 = 1 f(1,0,1) = a000 ⊕ a100 ⊕ a001 ⊕ a101 = 0 ⊕ 1 ⊕ 1 ⊕ a101 = 0 ⇒ a101 = 0 f(0,1,1) = a000 ⊕ a010 ⊕ a001 ⊕ a011 = 0 ⊕ 0 ⊕ 1 ⊕ a011 = 1 ⇒ a011 = 0 f(1,1,1) = a000 ⊕ a100 ⊕ a010 ⊕ a001 ⊕ a110 ⊕ a101 ⊕ a011 ⊕ a111 = 0 ⊕ 1 ⊕ 0 ⊕ 1 ⊕ 1 ⊕ 0 ⊕ 0 ⊕ a111 = 1 ⇒a111 = 0, тогда f= 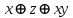 Способ 2. Найдём полином Жегалкина данной функции, исходя из формулы: 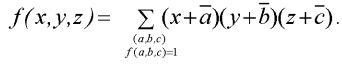 Получаем 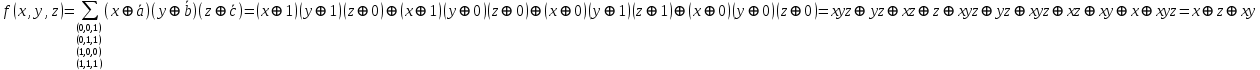 СДНФ (по единицам функции) 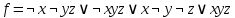 СКНФ (по нулям функции)  |
