Конспект. Конспект урока по алгебре в 9 классе на тему _Абсолютная и относ. Абсолютная и относительная погрешности
 Скачать 44.76 Kb. Скачать 44.76 Kb.
|
|
Тема урока Абсолютная и относительная погрешности Подготовила: учитель математики МБОУ Ужовской СШ Ухренкова Т.А. класс 9 Тип урока Урок изучения нового материала. Формируемые результаты Предметные: формировать умение оперировать понятиями «точное значение величины», «абсолютная погрешность», «относительная погрешность», сформировать понятие о приближённых вычислениях. Личностные: формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики. Метапредметные: формировать умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни. Планируемые результаты Учащийся научится оперировать понятиями «точное значение величины», «абсолютная погрешность», «относительная погрешность». Основные понятия Точное значение величины, абсолютная погрешность, относительная погрешность. Ход урока: 1. Организационный этап 2. Постановка формируемых результатов урока. Мотивация учебной деятельности учащихся 3. Актуализация знаний Устно. № 1. Округлите число 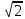 до: до:1) целых; (1) 2) десятых; (1,4) 3) сотых. (1,41) № 2. Округлите число 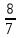 до: до: 1) целых; (1) 2) десятых; (1,1) 3) сотых (1,14) 4. Изучение нового материала § 16 Практическая деятельность человека неразрывно связана с числами, которые можно получать тремя способами: в результате измерений, счета и выполнения математических операций. Однако: - Любое измерение нельзя выполнить точно: ошибку дает либо прибор, либо наблюдатель. - Счет дает точные результаты, только если количество предметов невелико и если оно постоянно во времени. - Далеко не все математические операции можно выполнить абсолютно точно. В этих случаях мы имеем дело с приближенными числами. Но при вычислениях важно знать отклонение приближенного значения величины от ее точного значения, для этого вводится понятие абсолютной погрешности приближения. Определение. Абсолютной погрешностью приближения называется модуль разности между точным значением величины и ее приближенным значением. Δ = 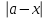 , где Δ – абсолютная погрешность , где Δ – абсолютная погрешностьa – точное значение величины x – приближенное значение Δ = 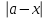 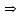 a - x= a - x= 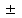 Δ Δ 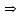 a = x a = x 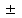 Δ ΔПример. Найти абсолютную погрешность приближения 0,44 числа 4/9. Δ = 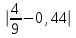 = = 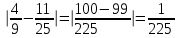 На практике во многих случаях точное значение бывает неизвестно, поэтому абсолютную погрешность найти нельзя. Однако можно дать оценку абсолютной погрешности, если известны приближения с избытком и с недостатком. Определение Границей абсолютной погрешности Δ приближения называется такое положительное число h больше которого абсолютная погрешность быть не может. Δ = 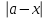 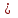 h hПример. 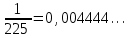 < 0,0045 < 0,0045x - Δ – Нижняя граница (Н.Г.) x + Δ – Верхняя граница (В.Г.) Приближенные числа, как и точные записываются как правило при помощи десятичных дробей. Но если в записи точного числа все его цифры верные, то в приближенном некоторые его цифры верные, а другие являются сомнительными. Определение. Цифра называется верной (точно значащей), если абсолютная погрешность числа не превосходит единицы того разряда в котором записана эта цифра. В противном случае она называется сомнительной. Пример. x = 3,7412 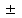 0,002 0,002Определить верные и сомнительные цифры. В.Г. = 3,7412 + 0,002 = 3,7432 Н.Г. = 3,7412 - 0,002 = 3,7392 Верные – 3 и 7, сомнительные 4,1 и 2. Замечания. В записи приближенного числа сохраняются только верные цифры. x = 3,7 Если в десятичной дроби последние верные цифры нули, то они остаются в записи числа. x = 0,301 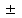 0,001 0,001 В.Г. = 0,302 Н.Г. = 0, 300 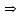 x = 0,30 x = 0,303) В десятичной записи числа значащими цифрами называются все его верные цифры, начиная с первой слева отличной от нуля. 0, 583; 38,57; 38,507; 29,830 Правило округления чисел: Если первая слева отбрасываемая цифра меньше 5, то округляют с недостатком, если это цифра 5 или больше, то округляют с избытком. Пример. 5,739 (с точностью до 0,01) 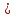 5,74 5,743, 53 (с точностью до целых) 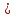 4 430253 (с точностью до 1000) 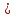 30000 30000Но абсолютной погрешности не достаточно для полной характеристики приближения. Если измерять расстояние между двумя городами, которое равно 100 км, с точность до 1 м, то это будет точное измерение, а если с точность до 1м измерена длина участка земли, которая равна 10м, то это грубое измерение. Определение. Относительной погрешностью называется отношение абсолютной погрешности к приближенному значению измеряемой величины. Обычно выражается в процентах. ω = 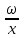 ; ω% = ; ω% = 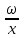 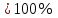 Т.о. для более полной оценки точности измерений необходимо определить, какую часть, или сколько процентов, составляет абсолютная погрешность от значения данной величины. Пример. Сравнить точность двух измерений . d = 4 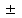 0,3; H = 600 0,3; H = 600 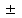 0,3 0,3ω(d) = 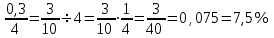 ω(H) = 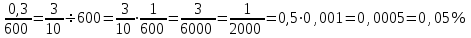 Второе измерение более точное. 5. Первичное закрепление нового материала № 555−558, 560 Дополнительно № 155, 156 6. Рефлексия учебной деятельности на уроке Продолжите высказывания об уроке. 1. Знания, полученные на уроке, мне необходимы … . 2. Я получил(а) полезную информацию о том, что … . 7. Информация о домашнем задании § 16, вопросы 1, 2, № 559, 561 |
