Курсовая работа. курсовя. Академия биоресурсов и природопользования факультет землеустройства и геодезии
 Скачать 2.35 Mb. Скачать 2.35 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего образования «КРЫМСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ имени В. И. Вернадского» (ФГАОУ ВО «КФУ им. В. И. Вернадского») АКАДЕМИЯ БИОРЕСУРСОВ И ПРИРОДОПОЛЬЗОВАНИЯ ФАКУЛЬТЕТ ЗЕМЛЕУСТРОЙСТВА И ГЕОДЕЗИИ Кафедра геодезии и геоинформатики Свистун Артем Олегович Особенности цифрового трансформирования и составление фотопланов Курсовой проект Обучающегося 3 курса Направления подготовки 21.03.03 «Геодезия и дистанционное зондирование» Форма обучения очная Руководитель должность, учёная степень, звание ст. пр. В. А. Нечаев Симферополь, 2019 Содержание
Цифровое трансформирование снимков 1.1. Назначение и области применения цифрового трансформирования снимков Трансформированием снимков в фотограмметрии называют процесс преобразования исходного снимка объекта в изображение объекта в заданной проекции. При цифровом трансформировании исходный снимок представляет собой цифровое изображение, получаемое или непосредственно цифровой съемочной системой или путем преобразования аналогового снимка в цифровую форму на сканере. Основными областями применения цифрового трансформирования являются топография и картография. При создании и обновлении карт различного назначения по аэрокосмическим снимкам создаются трансформированные изображения местности в проекции карты. Эти изображения могут быть созданы по одиночным снимкам или по нескольким перекрывающимся снимкам. Цифровое трансформирование выполняется с точностью, соответствующей точности, предъявляемой действующими нормативными документами к точности карт соответствующего масштаба. Цифровые трансформированные изображения используют для создания контурной части карт, путем векторизации цифровых изображений в среде CAD или ГИС, а также как самостоятельные картографические документы. В частном случае, если при трансформировании снимков не учитывается влияние кривизны Земли и проекции карты на положение контуров, трансформированное изображение представляет собой ортогональную проекцию местности на горизонтальную плоскость. Такой вид трансформирования называется ортофототрансформированием. Помимо топографии и картографии, цифровое трансформирование используется для создания по исходным снимкам перспективных изображений местности из заданных точек пространства. Такие изображения используют в военной области, например, в летных тренажерах и в архитектуре - при проектировании различных сооружений. Цифровое трансформирование применяют также для преобразования стереопар исходных снимков в стереопару снимков идеального случая съемки в системе координат фотограмметрической модели. Такое преобразование выполняется в цифровых стереофотограмметрических системах. В настоящей главе рассматриваются теоретические основы цифрового фототрансформирования снимков, в частности, методы наблюдения и измерения цифровых снимков и методы создания цифровых трансформированных снимков и фотопланов. 1.2. Методы создания цифровых трансформированных изображений местности (объекта). Рассмотрим процесс цифрового трансформирования исходного снимка на примере его преобразования в цифровое трансформированное изображение, представляющее собой ортогональную проекцию местности на горизонтальную плоскость (ортофотоснимок). Принципиальная схема этого процесса представлена на рис.1.1. В результате цифрового трансформирования исходный снимок преобразуется в цифровое изображение местности, представляющее собой ортогональную проекцию местности на горизонтальную плоскость. Принципиальная схема цифрового трансформирования снимков.  Рис.1.1 Исходными материалами при цифровом трансформировании снимков служат: цифровое изображение исходного фотоснимка; цифровая модель рельефа (ЦМР) значение элементов внутреннего и внешнего ориентирования снимков; значение параметров внутреннего ориентирования снимка в системе координат цифрового изображения. В большинстве случаев при трансформировании снимков используется цифровая модель местности в виде матрицы высот, представляющей собой регулярную сетку квадратов на местности, стороны которых параллельны осям XиYсистемы координат объекта 0XYZ. Координаты и высоты узлов сетки квадратов определены в системе координат объекта. Для формирования ЦМР в виде матрицы высот, в большинстве случаев, используют цифровые модели рельефа, созданные в результате стереофотограмметрической обработки снимков или по уже существующим топографическим картам. Наиболее распространённым методом построения цифровых моделей рельефа местности является, в настоящее время, метод триангуляции Делоне, в котором рельеф местности представлен в виде пространственной сети треугольников, координаты и высоты вершин которых определены в системе координат объекта. Рельеф местности в пределах треугольника в этом виде ЦМР, аппроксимируется плоскостью, проведённой через его вершины. При формировании ЦМР этим методом по высотным пикетам треугольники генерируются под условием, чтобы в окружность, проведенную через вершины треугольников, не должны попадать вершины других треугольников. По  цифровой модели рельефа в виде триангуляции Делоне можно сформировать ЦМР в виде матрицы высот. цифровой модели рельефа в виде триангуляции Делоне можно сформировать ЦМР в виде матрицы высот.р Для определения высоты узла i матрицы высот, по координатам xi и yi этого узла в системе координат объекта находят вершины треугольника триангуляции Делоне, в котором находится узел I (рис.1.2). Значение высоты узла i определяют по формуле: Zi = A + BXi + CYi (_1.1) Выражение (_2.1) представляет собой уравнение плоскости проведенной через вершины треугольника, внутри которого находится узел i. Коэффициенты уравнения (_1.1) A, B и C получают в результате решения системы из трёх уравнений A + BX + CY ─ Z = 0 , составленных по значениям координат X, Y и высот Z каждой из вершин треугольника. Цифровое трансформирование снимка выполняется следующим образом. Сначала формируется прямоугольная матрица цифрового трансформированного изображения, строки и столбцы которой параллельны осям XиYсистемы координат объекта, а координаты одного из углов матрицы заданы в этой же системе координат. Размер элементов (пикселей) матрицы обычно выбирают приблизительно равной величине×m, в которой: - - размер пикселя цифрового изображения исходного снимка; - m - знаменатель среднего масштаба снимка. Значения координат начала системы координат создаваемой матрицы, выбирают кратными величине элементов матрицы. Для формирования цифрового трансформированного изображения, каждому элементу цифрового изображения aij необходимо присвоить оптическую плотность изображения соответствующего участка объекта на исходном цифровом снимке. Эта операция выполняется следующим образом. По значениям индексов i и j элементов матрицы aij определяются координаты X, Y центра соответствующего пикселя цифрового трансформированного изображения в системе координат объекта. По координатам Xi, Yi точки объекта, соответствующей центру пикселя, по цифровой модели рельефа определяется высота этой точки Zi. Определение значения Zi по ЦМР в виде матрицы высот выполняется методом билинейного интерполирования (рис.1.3).  Рис.1.3 На рис.1.3 X = Xi - X1, а Y= Yi - Y1, где X1 и Y1 - координаты узла 1 цифровой модели рельефа. Высота точки Zi вычисляется по формуле: в которой:  . .По координатам Xi, Yi, Zi и значениям элементов внутреннего и внешнего ориентирования снимка вычисляются координаты х,у соответствующей точки на исходном цифровом снимке в системе координат снимка Sхуz. Вычисления производятся по формулам:  , (1.3) , (1.3)в которых  . .По координатам х,у и значениям параметров внутреннего ориентирования цифрового изображения определяют координаты точки снимка в системе координат цифрового изображения осхсус. В случае использования аффинных преобразований при выполнении внутреннего ориентирования, определение координат выполняется по формулам: 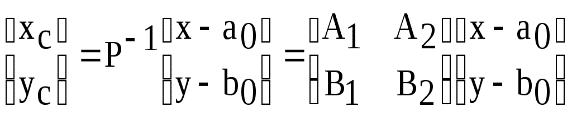 Затем по координатам хС и уС вычисляются пиксельные координаты точки  . .По значениям пиксельных координат xp,ypточки цифрового изображения снимка, которая является проекцией центра пикселя матрицы цифрового трансформированного изображения, находят ближайшие к этой точке четыре пикселя цифрового изображения снимка. А затем, методом билинейной интерполяции, изложенным в разделе 1.1, по формулам (1.7) определяют значение оптической плотностиDiили цвета соответствующего пикселя матрицы цифрового трансформированного изображения. При этом значение величинхp,yp в формулах (1.7) определяют по формулам:  . .Таким же образом определяются оптические плотности или цвет всех остальных пикселей цифрового трансформированного изображения. Помимо метода билинейной интерполяции для формирования цифрового трансформированного изображения применяют метод “ближайшего соседа”, в котором по пиксельным координатам xp,ypнаходят пиксель цифрового изображения снимка, на который проектируется точка, соответствующая центру пикселя цифрового трансформированного изображения, и значение его оптической плотности или цвета присваивается пикселю цифрового трансформированного изображения. Метод “ближайшего соседа” позволяет сократить время формирования цифрового трансформированного изображения по сравнению с методом билинейной интерполяции, однако изобразительные свойства формируемого цифрового изображения при этом ухудшаются. Если превышения точек на участке местности, изображенной на снимке, незначительны, при создании цифрового трансформированного изображения значения высот точек местности, соответствующих центрам пикселей трансформированного изображения, принимаются равными среднему значению высоты участка местности. В этом случае, нет необходимости в создании цифровой модели рельефа местности, так как трансформированное цифровое изображение представляет собой центральную проекцию исходного снимка на горизонтальную плоскость, расположенную на высоте Z, равной среднему значению высоты участка местности. Такой метод трансформирования допустим в случае, если ошибки в положении точек на трансформированном изображении, вызываемые рельефом местности, не превышают допустимых значений. Величины максимально допустимых значений превышений точек местности – h max относительно средней плоскости, при которых ошибки в положении точек на трансформированном изображении не будут превышать установленного допуска R max , можно определить по формуле : h max = в которой : f – фокусное расстояние съёмочной камеры; r – расстояние на исходном снимке от главной точки до точки на снимке. Как следует из формулы 1.4, величина ошибки, Rmax прямо пропорционально значению r. Поэтому при определении hmax измеряется значение r до наиболее удаленной от главной точки снимка точки, участвующей в формировании трансформированного изображения. Следует отметить, что формулы (1.4) используют только в случае, если трансформирование выполняется по снимкам, углы наклона которых не превышают 3 - 5. Аналогичным образом можно определить величину допустимой ошибки hmax определения высот точек местности, соответствующих центрам пикселей трансформированного изображения, по цифровой модели рельефа. hmax = В случае, если трансформирование снимков выполняется с целью создания или обновления карт и планов значение Rmax выбирается равной величине 0,2 мм на карте или плане. То есть Rmax = 0.2мм · M , где М – знаменатель масштаба создаваемой карты. При создании цифровых трансформированных изображений местности в проекции карты, плановые координаты узлов цифровой модели рельефа определяют в системе координат карты. В России топографические карты создаются в проекции Гаусса - Крюгера в государственных системах координат СК 42, СК 63 и СК 95. Высоты узлов цифровой модели рельефа задают равными геодезическим высотам Hэтих узлов относительно поверхности референц – эллипсоида. По значениям координат узлов x,yв государственной системе координат вычисляют значения геодезической широты В и долготыLузлов цифровой модели рельефа, а затем по величинамB, L иH, координаты узловXгц,YгциZгц в геоцентрической системе координат. Эти преобразования подробно изложены в курсах высшей геодезии и математической картографии. В остальном, процесс цифрового трансформирования аналогичен процессу создания цифрового ортофотоизображения. Необходимо только отметить, что элементы внешнего ориентирования снимка, в этом случае, должны быть определены в геоцентрической системе координат. Вместо геоцентрической системы координат можно использовать топоцентрическую систему координат OтцXтцYтцZтц. Начало топоцентрической системы координат обычно выбирают в середине обрабатываемого участка местности. ОсьXтц топоцентрической системы координат лежит в плоскости меридиана, проходящего через начало системы координат. ОсьZтц совпадает с нормалью к поверхности референц –эллипсоида в начале системы координат, а осьYтц дополняет систему до правой. При использовании топоцентрической системы координат, элементы внешнего ориентирования исходного снимка должны быть определены в этой системе координат. 2.Дешефрирование аэрофотоснимка 2.1. Лист карты номенклатуры L-36-119-a На Рис. 2.1. отмечены четверть – вторая и населенный пункт - Наниково, в которых выполнялось практическое задание На данном этапе была выполнена привязка карты по пяти пунктам Государственной Геодезической Сети, координаты которых были взяты в программе QGis.  Рис. 2.1. 2.2.Аэрофотоснимок населенного пункта Наниково Следующий этап – создание аэрофотоснимка в программе Google Earth и привязка данного снимка. Привязка была выполнена с помощью фигуры, начерченной на листе карты по видимым точкам и на карте, и на снимке. Далее были выполнено внешнее ориентирование, в результате которого и был привязан снимок.  Рис. 2.2. 2.3.Дешифрирование аэрофотоснимка населенного пункта Наниково Дешифрирование снимка было выполнено при использовании функции «сбор» и использовании различных слоев, представленных в программеDigitals.  Рис. 2.3.  Рис. 2.4. Заключение В ходе написания курсовой работы был рассмотрен вопрос в работе рассмотрены принципиальные вопросы сущности и содержания фотопланов и ортофотопланов. Доказано, что нет смыслового различия между фотопланами и ортофотопланами. Фотопланы создают на равнинную местность, а ортофотопланы — на горную. по своим пользовательским свойствам они должны отвечать единым требованиям. Различные названия являются следствием применяемых способов и технологий трансформирования снимков, которые особенно проявлялись на этапах развития аналоговой и аналитической фотограмметрии. Список литературы 1. Лобанов А.Н. Фотограмметрия: Учебник для вузов. М.: Недра, 1984 2.Назаров А.С. Фотограмметрия: учебное пособие для студентов вузов. — Минск: ТетраСистемс, 2006 3.Павлов В.И. Конспект лекций по дисциплине «Прикладная фотограмметрия». Санкт-Петербургский государственный горный университет. СПб, 2009. 4.Павлов В. И. Прикладная фотограмметрия. Методические указания к курсовой работе для студентов специальностей 120101 и 120303. Санкт-Петербургский государственный горный университет. СПб, 2009. 5.Павлов В.И. Фотограмметрия. Теория одиночного снимка и стереоскопической пары снимков. Санкт-Петербургский государственный горный университет. СПб, 2006 |
