программирование. Алашы функция. Аныталмаан интеграл, оны асиеттері Туындысы бойынша функцияны табу жніндегі есептер
 Скачать 4.35 Mb.
|
|
Саткулова Мадина Бактыбаевна Математика-Инфоматика (503) гр Студенттің өзіндік жұмысы-4 "Алғашқы функция және интеграл" тақырыбына логикалық-математикалық талдау жасау. Алғашқы функция. Анықталмаған интеграл, оның қасиеттері 1. Туындысы бойынша функцияны табу жөніндегі есептер. Біз берілген туындысы бойынша функцияның өзін табумен байланысты екі есептің шешімін таппақпыз. 1. Дененің қозғалыс заңы S=f(t) теңдеу арқылы берілген. Бұндағы t-уақыт, s-дененің жүрген жолы. Қарастырылып отырған қозғалыстың берілген мезгілдегі лездік жылдамдығы v: 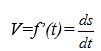 формуласы бойынша анықталатыны дифференциалдық есептеуден белгілі болатын. Ал механикада бұған кері есеппен тым жиі кездесуге тура келеді. Ондай есептер мына түрде болып келеді; дененің берілген t мезгіліндегі туындысы v=v(t) беріледі де, сол бойынша дененің қозғалу заңын табу, яғни өткен мерзім мен жүрген жол арасындағы тәуелділікті анықтау талап етіледі. Бұл есептің шешімі былай табылады: Берілген жылдамдық v=v(t) дененің қозғалыс заңын бейнелейтін f(t) функциясының туындысы болатыны бізге белгілі, демек ізделіп отырған белгісіз функция f(t)-тің туындысы f’(t)=v(t) берілген. Бізден сол f(t)-ті табу талап етіледі. Демек, бұл есеп дифференциалдық есептеуде қарастырылған негізгі есепке кері есеп болып табылады. Басқаша айтқанда: дифференциалдық есептеуде функция беріліп, оның туындысын табу талап етілсе, енді туынды беріледі де, бастапқы функцияны табу етіледі. 2.[0, i] кесіндісіне орналасқан дененің сол кесіндінің х нүктесіндегі  сызықтық тығыздығы p: функциясы түрінде беріледі. Енді сол дененің [0, i] кесіндісінің [0, x] бөлігіндегі тығыздығы m-ді табу керек. [0,x] бөлігінің массасы - x- тің функциясы, яғни m=f(x). Олай болса, массасын табу дегеніміз осы f(x) функциясын табу болып табылады. x нүктесіндегі сызықтық тығыздық p: 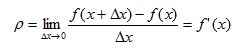 формуласымен анықталады. Ендеше,  болады. Ал есептің шарты бойынша  -белгілі функция, демек берілген сызықтық тығыздығы бойынша дененің массасын табу дегеніміз берілген туынды f’(x) бойынша функция f(x)- ті табу жөніндегі мәселе болады.2. Алғашқы функция ұғымы. Ғылым мен техниканың түрлі-түрлі салаларындағы көптеген мәселелерді шешу туындысы берілген функцияны табуға әкеліп соқтырады. Сондықтан математикада жаңа бір операция, интегралдау операциясы қарастырылады. Ізделіп отырған F(x) функциясының берілген туындысы f(x) бойынша сол F(x) функциясын табу мәселесі тек интегралдау операциясының жәрдемімен шешіледі. Міне осы F(x)-ті берілген функция f(x)-тің алғашқы функциясы деп атайды. Анықтама. Егер бір аралықтың әрбір нүктесінде функция F(x) үшін dF(x)=f(x)dx теңдігі орындалса, F(x) функциясы f(x)-тің сол аралықтағы алғашқы функциясы деп аталады. Мысалы: F(x)=x7 бүкіл сандар осі бойында f(x)=7x6 функциясының алғашқы функциясы болады, өйткені х-тің кез келген мәнінде (x7)’=7x6. Ал функция F(x)=lnx функция f(x)=1/x үшін алғашқы функция болады өйткені (lnx)’=1/x 1-теорема. Егер F(x) функциясы белгілі бір аралықта f(x)-тің алғашқы функциясы болса, F(x)+c Функциясыда (C- кез келген тұрақты) ол функция үшін сол аралықта алғашқы функция болады. Дәлеледеу: F(x) функциясы f(x) –тің алғашқы функциясы. Олай болса, F’(x)=f(x). Сонымен бірге [F(x)+C]’=f(x) Демек F(x)+C функциясы да f(x) үшін алғашқы функция болады. 2 теорема. Берілген функцияның алғашқы функцияларының бір-бірінен айырмасы тұрақты шама болады. Дәлелдеу. Егер берілген f(x) функциясының қандай да бір алғашқы функциясының F(x), ал, кез келген алғашқы функциясын  десек, онда мына шарттар орындалар еді:  яғни алынған аралықта F(x) пен функцияларының туындылары бірдей болады. Олай болса,  айырымы тұрақты болуы тиіс, яғни:  Бұдан  Дәлелденген екі теоремадан мынадай қорытынды шығады: егер F(x) функциясы белгілі аралықта f(x)–тің алғашқы функцияларының бірі болса, оның барлық алғашқы функцияларының жиыны f(x)+С қосындысымен өрнектеледі. Қосындының геометриялық мағнасы: f(x)-тің алғашқы функциясы F(x)-тің графигін жоғары не төмен жылжыту арқылы кез келген алғашқы функцияның графигін сала аламыз (1 сызба). 3. Анықталмаған интеграл ұғымы F(x) функциясы дифференциалдау деп берілген алғашқы F(x) функциясының F’(x)= f(x) туындысын немесе df(x)=f(x)dx Дифференциалын табу амалын айтамыз. Сол амалға кері амал, яғни F’(x) болып табылатын берілген f(x) үшін алғашқы F(x) функциясын табу амалы f(x)-ті интегралдау деп аталады. f(x)-ті интегралдау амалын көрсету үшін  символы қолданылады да, былай жазылады: Осы берілген f(x) функциясының барлық алғашқы функцияларының жиынын бейнелейді және f(x)-тен анықталмаған интеграл деп аталады.Демек, анықтамаға сәйкес  болады. Бұл формуладағы F(x) функциясы f(x)-тың белгілі бір алғашқы функциясы, С-кез келген тұрақты. Сонымен бірге f(x)- интеграл астындағы функция, ал f(x)dx – интеграл астындағы өрнек деп аталады. -символы ұзартылып алынған латын алфавитіндегі S- әріпі, ол символды интегралдың белгісі деп атайды.Функцияны интегралдау және олардың алғашқы функцияларының қаиеттері жайындағы ілім интегралдық есептеу деп аталады. Дифференциалдық есептеу сияқты интегралдық есептеуде математикалық анализдің өте маңызды бөлімдерінің бірі болып табылды. 1-параграфта қарастырылған есептердің шешуін енді интеграл түрінде былай жазуға болады: 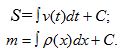 4. Анықталмаған интегралдың негізгі қасиеттері F’(x)=f(x) және  екенін ескере отырып анықталмаған интегралдың қасиеттерін қарастырамыз.1. Дифференциалдың анықталмаған интегралы дифференциалдаған функция мен кез келген тұрақтының қосындысына тең, яғни  2. Анықталмаған интегралдың дифференциалын интеграл астындағы өрнекке тең, яғни  3. Тұрақты көбейткішті интегралдық белгінің алдына шығаруға да, интегралдық белгінің астына алып баруға да болады, яғни  4. Бірнеше функциялардың алгебралық қосындының анықталмаған интегралы қосылғыштардан алынған анықталмаған интегралдардың алгебралық қосындысына тең, яғни  5. Анықталмаған интегралдың негізгі таблицасы Егер u аргумент х-тің белгілі бір аралықтағы дифференциалданатын функциясы болса, берілген дифференциалдық есептеудің формулаларын пайдаланып, анықталмаған интегралдың ішіндегі негізгілерінің таблицасын жасауға болады. Бұл таблицаға енетін әрбір формуланың дұрыстығын дифференциалдау арқылы дәлелдеп көрсетуге болады.   Осы көрсетілген форуларды пайдаланып функцияның анықталмаған интегралын табуға мысалдар қарастырайық: 1.  интегралын есептеу керек.Шешуі. (3) формула бойынша 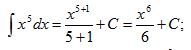 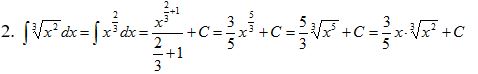  интегралын табу керек.Шешуі: Интеграл астындағы өрнекті жақшаны ашып мына түрге келтіреміз:  Қосындының интегралын интегралдардың қосындысымен ауыстырсақ,  боладыҮшінші интегралдағы тұрақты көбейткішті интеграл табысының алдына шығарсақ,  түрге келеді(2) және (3) формулаларды қолдансақ  4. 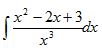 интегралын табу керекШешуі: Бөлшектің алымын бөліміне мүшелеп бөліп, алдыңғы мысалдағыдай есептейміз 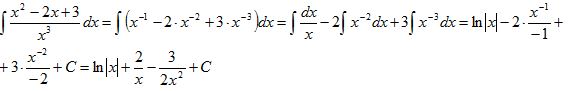 Берілген интегралды интенгралдардың қосындысына келтіріп интегралдау қосындысына келтіріп интегралдау әдісін жіктеу әдісі деп атайды. Қарастырылған 3 және 4 мысалдар жіктеу әдісімен шығарылады. Сабақтың тақырыбы: Туынды тақырыбын қайталау Сабақтың мақсаты: Оқушылардың есеп шығару дағдыларын қалыптастыру. Міндеттері: Білімділік: Оқушының туындыға қатысты білімін, туынды ережелерін қолдану шеберлігін, дағдыларын бақылау, тексеру.Туынды ұғымы бойынша оқушылардың ойлауын дамытуға, пәнді оқып үйренуге қажетті білім, білік және іскерлік дағдыларын меңгеруді бекітуге бағытталған; Дамытушылық: Оқушылардың логикалық ойлауын, математикалық дүниетанымын кеңейту; Тәрбиелік: Оқушылардың бір-біріне көмектесу адамгершілігін,өзіндік дүниетанымын қалыптастыру. Сабақтың түрі: Қайталау сабағы. Сабақтың көрнекілігі: Электронды оқулық, слайд, семантикалық карта, үлестірме қағаздар т.б Пәнаралық байланыс: Физика, тарих Сабақтың жоспары: Ұйымдастыру кезеңі 3 мин. Қайталау (флипчартпен жұмыс) 5 мин. Оқулықпен жұмыс. 15мин. Тарихи мәлімет 3мин. Кестемен жұмыс 5мин. Электронды оқулықпен жұмыс (тест) 6 мин. Сабақты қорытындылау 3 мин. Бағалау 3мин. Үй тапсырмасын беру 2мин. «Халық пен халықты, адам мен адамды теңестіретін нәрсе-білім» М.Әуезов Сабақтың барысы: І. Ұйымдастыру кезеңі: Оқушылармен сәлемдесу. Түгендеу.Назарларын сабаққа аудару. II. Қайталау сұрақтары: а) Туынды дегеніміз не? ә) Туындының белгіленуі б) у'(х) белгілеулерін енгізген кім? в) с;х; (хп)' – неге тең? г) Туындының қолданылуы? д) Дифференциалдау ережелері Функциялардың туындыларының формулаларын интерактивті тақтада сәйкестендіру (флипчартпен жұмыс) ІІІ. Оқулықпен жұмыс №144, №147, №154, №155 IV. Тарихи мәлімет. Дифференциалдық есептеудің негізгі ұғымы – туынды ұғымы – физика, механика және математика есептерін, атап айтсақ,түзусызықты бірқалыпсыз қозғалыстың жылдамдығы мен кез келген қисыққа жанама жүргізуге байланысты есептерді шешу кезінде XVII ғасырда пайда болды. XV-XVII ғасырларда математиктердің алдында кез келген нүктеге жанама жүргізудің жалпы әдісін табу мәселесі тұрды. Есептерді шешудің кейбір дербес жағдайлары ежелден-ақ белгілі болатын. Мысалы, Евлид бастамаларында шеңберге жанама жүргізу әдісі берілген, Архимед өз атымен аталатын шиыршыққа (спиралға) жанма жүргізсе, ал Аполоний – эллипс,гипербола және параболаға жүргізген. Алайда ежелгі грек ғалымдары есепті аяғына дейін шешкен жоқ, яғни қандай да бір қисықтың кез келген нүктесіне жанама жүргізудің тиімді жалпы әдісін таппады. V. Кестемен жұмыс.
VI. Электронды оқулықпен жұмыс. (тест) ҮII. Сабақты қорытындылау ҮIII. Оқушылар білімін бағалау. Жеке оқушыларды бағалау. ҮІ.Үй тапсырмасы: №142, №145, №1150, №156 (А.Е.Әбілқасымова, К.Д.Шойынбеков «Алгебра және анализ бастамалары-10», Мектеп,2006ж ) |
