СЛАУ. ПЗ-1с_19 СЛАУ. Алгебра & геометрия дисциплина и подготовка аудитории
 Скачать 190 Kb. Скачать 190 Kb.
|
|
АЛГЕБРА & ГЕОМЕТРИЯ Дисциплина и подготовка аудитории Организация обучения (Л-ПЗ-ДЗ-ТК) Текущий контроль (РАР-АР) и аттестация(20 б) Информационная поддержка (ИОП-@)
 СЗ-МЭ-1 СЗ-МЭ-1Практическое Занятие 1 СЛАУ 03-05.09.19 ДЗ-1: Задачник по АГ (файл) №1-4, 31, 32; 12, 17 Сборник СЗ-МЭ-1 №1.4, 1.8 МЭ-1 с.25-27, 34 конспекты доказ-в Системы линейных алгебраических уравнений (СЛАУ) Задача 1 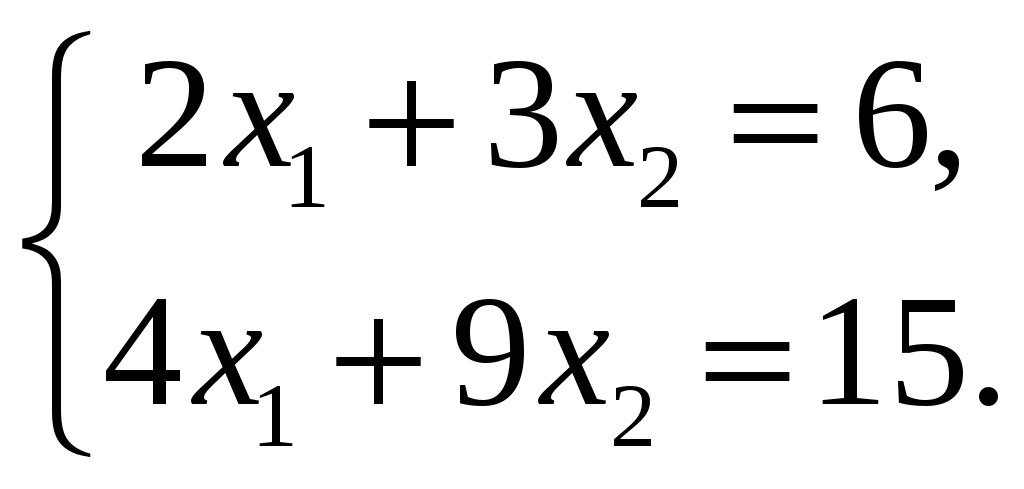 Ответ: (1,5; 1). 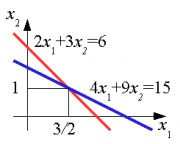 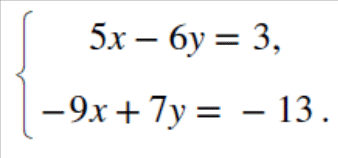 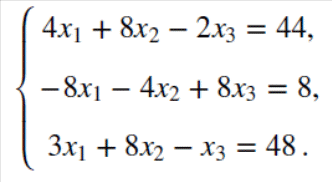 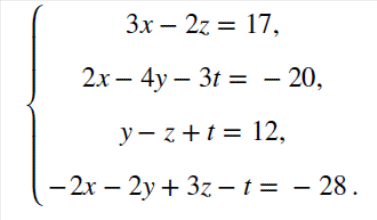 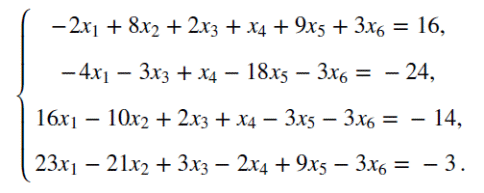 Решением СЛАУ называется упорядоченный набор n чисел 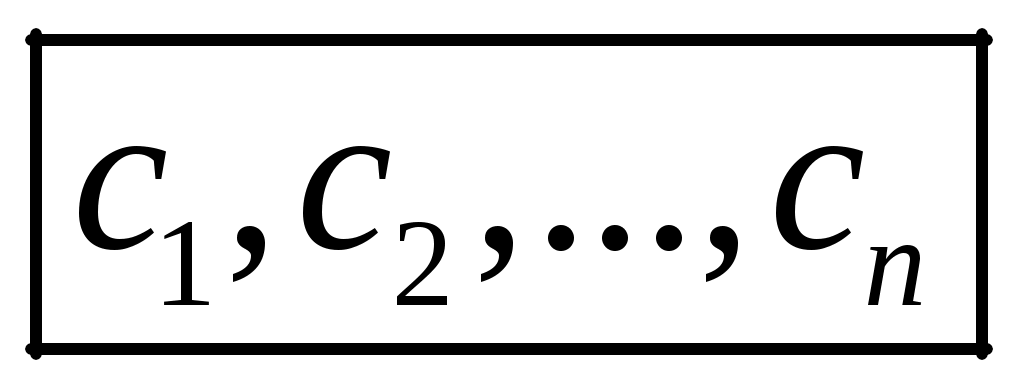 , подстановка которых вместо неизвестных обращает все уравнения в тождества. , подстановка которых вместо неизвестных обращает все уравнения в тождества.СЛАУ называется однородной (ОСЛАУ), если все ее свободные члены – нули. ОСЛАУ всегда совместна! СЛАУ называется совместной, если она имеет хотя бы одно решение (единственноеили бесконечное множество). ОСЛАУ всегда совместна! СЛАУ называется несовместной, если у нее нет ни одного решения. СЛАУ можно записать с помощью расширенной матрицы 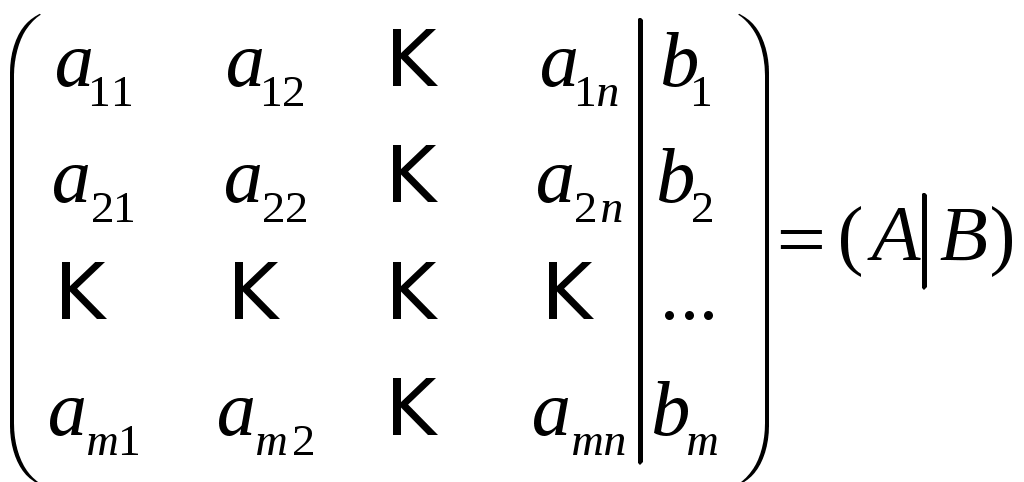 . .Элементарные преобразования расширенной матрицы ЭМ1: перестановка строк; ЭМ2:умножение строки на число, не равное нулю; ЭМ3: сложение строки с другой, умноженной на число; ЭМ4: добавление нулевой строки; ЭМ5: вычеркивание нулевой строки. Метод Гаусса – это универсальный алгоритмпоследовательного исключения неизвестных СЛАУ с помощью комбинированных элементарных преобразований расширенной матрицы. Используем модификацию, при которой добиваемся максимального исключения– метод Жордана-Гаусса. Задача 2 Решите систему линейных уравнений 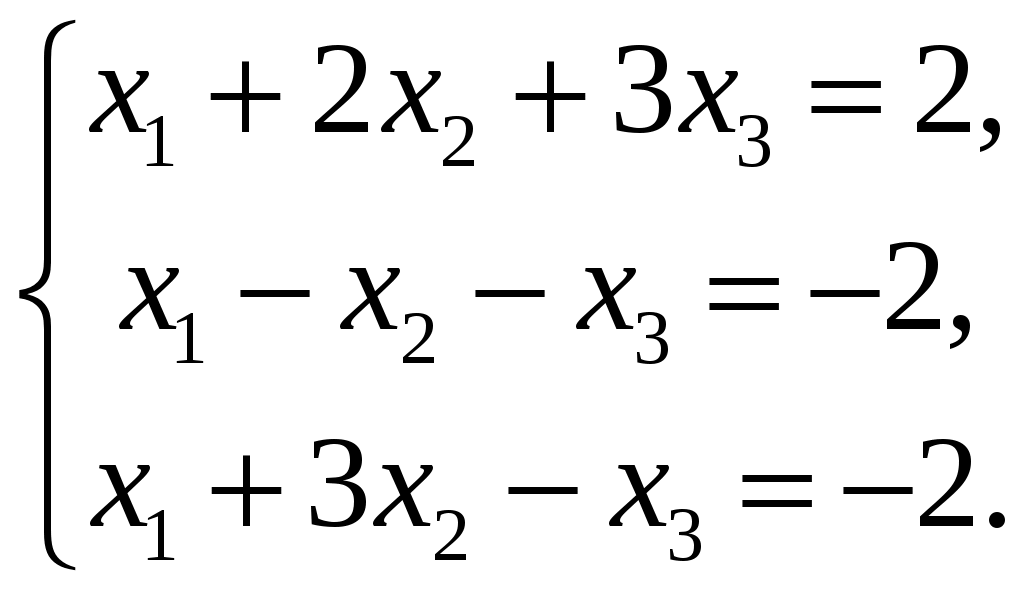 Ответ: (– 1; 0; 1). Шаги алгоритма: выбрать ненулевой разрешающий элемент в строке, не являвшейся разрешающей; все элементы разрешающей строки разделить на разрешающий; все элементы разрешающего столбца (кроме выбранного) заменить нулями; оставшиеся элементы пересчитать; вычеркнуть нулевые строки и проверить строки на совместность; выбрать новый разрешающий элемент (повторив для него пересчет) или выписать решение. Разрешающие столбцы в дальнейшем неизменны! Говорят, что эти столбцы (и соответствующие им неизвестные) становятся базисными. Остальные столбцы, не ставшие разрешающими (и соответствующие им неизвестные), называют свободными. Задача 3 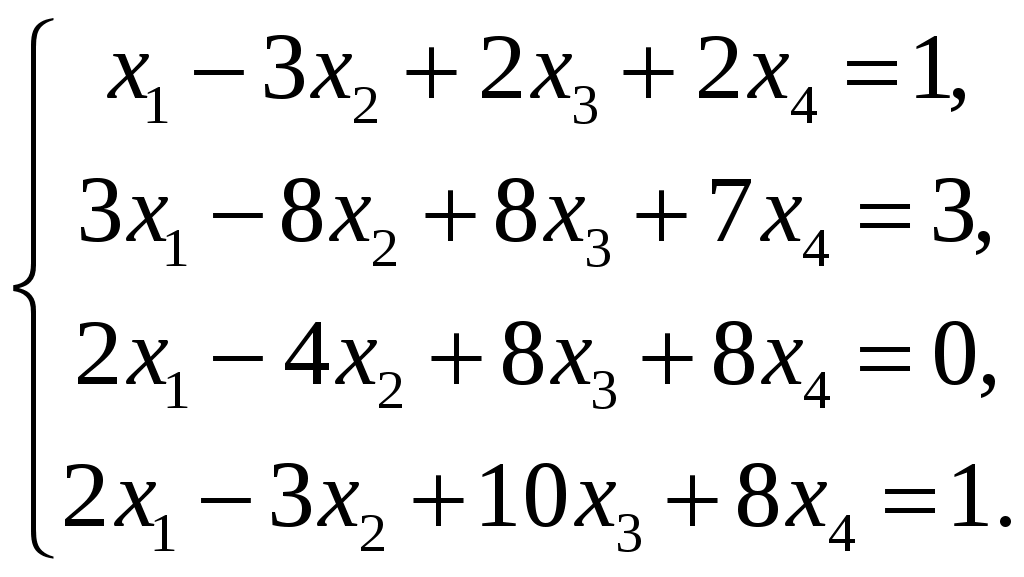 Ответ: 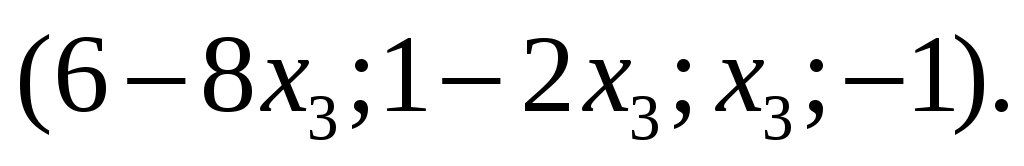 Общее и частное решение СЛАУ Общим решением СЛАУ называется совокупность всех решений, если базисные неизвестные выражены через свободные. Частным решением СЛАУ называется решение, если вместо свободных неизвестных подставлены числовые значения. Если вместо свободных неизвестных подставлены нули, то такое частное решение называется базисным. При различном выборе базисных неизвестных запись общего решения отличается, но в ответе указывают только один вариант! Для совместнойСЛАУ расширенная матрица преобразуется к одному из видов: диагональному (единственное решение), лестничному (бесконечное множество решений). Задания для самостоятельной работы Задача 4 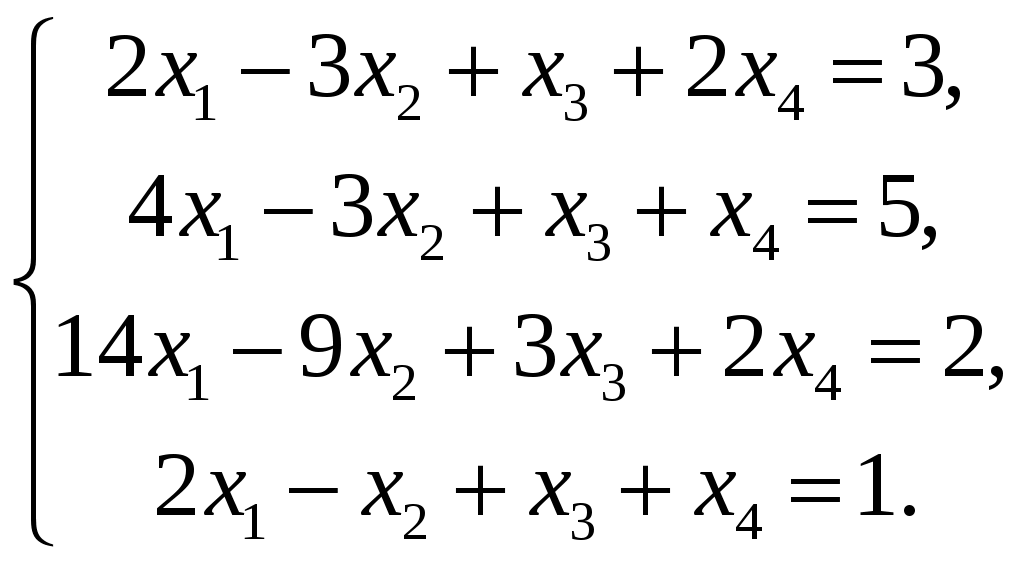 Ответ: нет решений. Задача 5 При каких значениях параметра система уравнений  а) неопределенная (имеет бесконечно много решений); б) определенная (имеет единственное решение); в) несовместна? Ответ: а) при 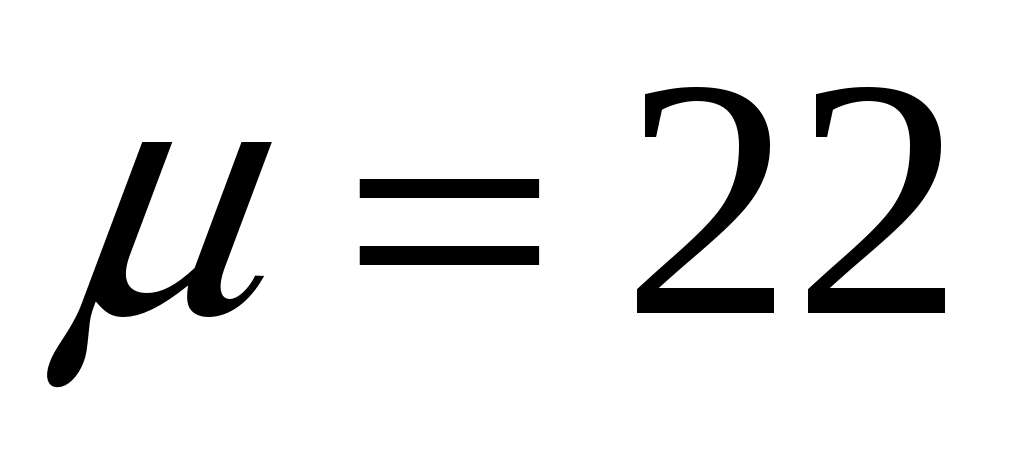 ; б) нет таких значений; в) при ; б) нет таких значений; в) при 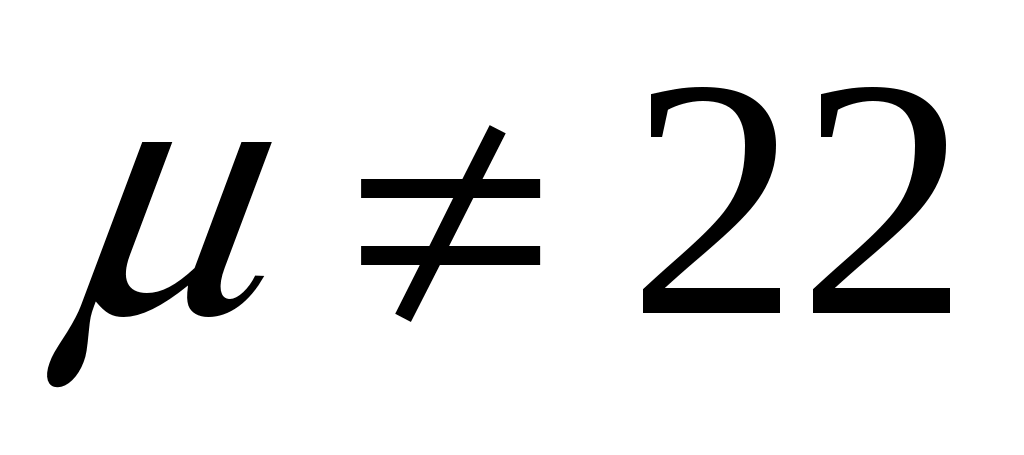 . . |
