разработки 8 класс. 8 кл. Алгебра. Учебник Алгебра, 8 класс Макарычев Ю. Н, Миндюк Н. Г. и др. Класс 8 Тип урока урок нового знания. Тема урока Квадратный корень. Арифметический квадратный корень. Оборудование учебник, проектор, компьютер
 Скачать 112.06 Kb. Скачать 112.06 Kb.
|
|
Учитель: Шогенова Рита Сарабиевна Предмет: алгебра. Учебник Алгебра, 8 класс Макарычев Ю.Н, Миндюк Н.Г. и др. Класс: 8 Тип урока: урок нового знания. Тема урока: Квадратный корень. Арифметический квадратный корень. Оборудование: учебник, проектор, компьютер. Цель: формирование понятий квадратный корень и арифметический квадратный корень. Форма организации учебной деятельности: фронтальная, индивидуальная, парная План урока: 1 этап. Организация класса 2 этап. Повторение изученного материала. 3 этап. Изучение нового материала 4 этап. Применение полученных знаний и умений (работа по учебнику, работа в парах, работа по карточкам) 5 этап. Рефлексия. Итоги урока. Выставление оценок. Ход урока 1.Организационный момент (2мин.) Проверка готовности к уроку. 2.Актуализация знаний (повторение изученного материала) (5 мин) - Наш урок хочется начать с восточной мудрости: « Можно коня привести к воде, но нельзя заставить его пить». Какой смысл скрывается в этом? Как вы это понимаете? (Ответы детей). Эту мудрость можно применить и к нам – людям. Ведь невозможно заставить учиться хорошо, если человек этого не хочет. Но вы должны понимать, что знания только тогда знания, когда они приобретены усилиями своей мысли, а не одной памятью. На прошлом уроке мы изучили темы «Рациональные и иррациональные числа». Сейчас с помощью математического диктанта вспомним пройденный материал. Ответим на вопросы: 1)Какие из чисел 351; -1253; -23,7; -1; 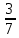 ; 12; 0; 32 ; 12; 0; 32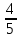 являются: являются: а) дробными б) натуральными в) целыми г) рациональными 2) С какими дробями вы ещё познакомились? Приведите пример. 3) Какие числа называются иррациональными? 4) Назовите самое известное иррациональное число? (число π) Ребята, оказывается, это число может звучать. Посмотрите, пожалуйста, ролик «Как звучит число π». Теперь мы можем двигаться вперед. 3.Изучение нового материала (15 мин) Послушайте стихотворение-загадку: Он есть у дерева, цветка, Он есть у уравнений, И знак особый – радикал – С ним связан, вне сомнений. Заданий многих он итог, И с этим мы не спорим, Надеемся, что каждый смог Ответить: это … (Корень) Сегодня мы рассмотрим понятие «корень» с точки зрения математики. Пусть дано уравнение Числа 5 и – 5 – квадратные корни числа 25, т.к. Какова тема сегодняшнего урока? (Запись темы урока в тетради): «Квадратный корень. Арифметический квадратный корень». Сформулируйте цель урока? Что каждый из вас должен усвоить и чему научиться? Вместо * вставьте числа, чтобы равенства были верными: *2 = 16 *2 = 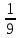 *2 = 100 *2 = 100Работа с учебником под руководством учителя (п.12 стр. 74-75) Определение: Квадратным корнем из числа а называют такое число, квадрат которого равен а. Действие, в результате которого находят квадратный корень из числа, называют извлечением квадратного корня. Квадрат никакого числа не может быть отрицательным. Поэтому, чтобы можно было извлечь квадратный корень из данного числа, необходимо, чтобы он был неотрицательным, т. е. это число должно быть или положительным или равным 0. Решим задачу: Площадь квадрата равна 81 см2. Чему равна длина стороны этого квадрата? Оба ли корня нам подходят по условию задачи? Почему? Определение: Положительный квадратный корень из неотрицательного числа называется его арифметическим квадратным корнем. Равенство Если № 298 (устно) Основное свойство арифметического квадратного корня: (√а)2 = а, если а ≥ 0 Например, (√3)2, (√49)2, (√ 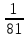 )2. )2.4.Физминутка 5.Применение полученных знаний и умений (работа по учебнику, работа в парах, работа по карточкам) (20 мин) № 299(устно) Давайте с вами подумаем: каким образом можно извлечь арифметический квадратный корень (вспомнить таблицу умножения, подобрать такое число, которое при умножении на само себя, дает подкоренное выражение) № 300 Знакомство с таблицей квадратов. № 306 (а,б) (работа в парах) А теперь предлагаю вам самостоятельно решить примеры карточек (на отдельных листах)
Проверка по ключу, самооценка. Дополнительный материал: Мы смотрим телевизор часами, целый день сидим за компьютером без перерывов, разговариваем по сотовому телефону без остановки, а потом не можем понять, почему же у нас так сильно болит голова и мы так устали, что ничего не видим. Помни! На компьютере рекомендуется работать не более 5.Рефлексия деятельности, домашнее задание (3 мин) Подведем итог работы на уроке. Что нового узнали сегодня на уроке? Надеюсь, что этот материал вы не забудете, он обязательно пригодится вам при дальнейшем изучении математики. Помните слова французского инженера-физика М.Лауэ: «Образование есть то, что остается, когда всё выученное уже забыто». Д.з.: п.12, № |

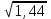 -2(
-2( 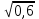 )2
)2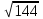 - 0,5 (
- 0,5 (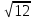 )2
)2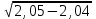
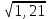
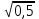 )
)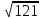
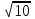 )
)