Алгоритм методу Ньютона-Рафсона. Курсова_дороб. Алгоритм методу НьютонаРафсона
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
|
ПОЯСНЮВАЛЬНА ЗАПИСКА ДО КУРСОВОЇ РОБОТИ З ПРОЕКТУВАННЯ АЛГОРИТМІВ ТА ПРОГРАМУВАННЯ на тему: «Алгоритм методу Ньютона-Рафсона» Зміст Вступ ……………………………………………………………………… 5 Основна частина…………………………………………………………. 7 Розділ 1. Алгоритм метода Ньютона-Рафсона загальні положення. 8 Розділ 2. Проектування програмного продукту …………………….. 10 Розділ 3. Реалізація програмного продукту ……………………………13 Висновок ………………………………………………………………….. 21 Список літератури ………………………………………………………. 22 Вступ Мета роботи: систематизація отриманих теоретичних знань з дисциплін «Проектування та аналіз алгоритмів», «Дискретні структури», «Чисельні методи», «Алгоритмізація та програмування», «Об’єктно-орієнтоване програмування», «Комп’ютерна графіка», «Операційні системи», «Технологія створення програмних продуктів», «Дослідження операцій», закріплення навичок самостійної роботи та поглиблення практичних навичок зі створення завершеного працездатного програмного продукту. Завдання: створити алгоритм для методу Ньютона-Рафсона, що призначений для оптимізації знаходження кореня дійсного рівняння Опис структури роботи за розділами: Перший розділ – аналітичний огляд інформаційних джерел, опис задачі, яка має вирішуватися в рамках курсової роботи, опис узагальненого алгоритму розв’язку задачі, переваги та недоліки методу, висновки, в яких буде формуватися ідеї програмного проекту та функціональні та не функціональні вимоги до нього; Другий розділ – проектування програмного продукту, де буде деталізована постановка задачі, що вирішується в рамках курсової роботи, опис методу та алгоритму розв’язку цієї задачі, опис основних структур даних, висновки, в яких ставиться задача на розробку програмного продукту; Третій розділ – реалізація програмного продукту, опис головних структур даних і змінних програми, функцій, структури програми, програмного інтерфейсу з користувачем та результати перевірки працездатності програмного продукту, висновки, в яких описується реалізований функціонал, аналіз результатів його тестування, виявлені недоліки тощо. Засоби розробки: Я збираюсь використовувати середовище «Pycharm studio», це середовище дозволяє вільно використовувати мову Python. Основна частина Розділ 1. Алгоритм метода Ньютона-Рафсона загальні положення Основна ідея градієнтних методів полягає в послідовних наближень до справжнього розв'язання рівняння f (x) = 0, які обчислюються за допомогою похідної від f (x). Основною ідеєю є введення нульової ітерації X0. В цій точці визначається похідна за методом кінцевих різниць. Користуючись розкладанням Тейлора, f (x) замінюється в околиці точки дотичній - прямою лінією f (x0) + f '(x0) (x-x0). Після цього визначається точка, в якій пряма перетинає вісь Х. Ця точка приймається за нову ітерацію, і цикл повторюється: будується дотична, точка її перетину з віссю і т.д., поки корінь не буде знайдений з потрібною точністю. Модифікація алгоритму Ньютона для розв'язання системи декількох рівнянь полягає в лінеаризації відповідних функцій багатьох змінних, тобто апроксимації їх лінійною залежністю за допомогою приватних похідних. Наприклад, для нульової ітерації у випадку системи двох рівнянь: 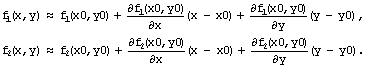 Щоб відшукати точку, відповідну кожної нової ітерації, потрібно прирівняти обидва рівності нулю, тобто вирішити на кожному кроці отриману систему лінійних рівнянь. На відміну від звичайного методу дотичних, в модифікованому методі надається менше вимог до вибору початкового наближення, а так само гарантовано відсутність поділу на нуль, якщо Однак модифікований метод має один істотний недолік: лінійну швидкість збіжності: Збіжність методу: Слід замітити, що метод дотичних є окремим випадком методу простих ітерацій Метод простих ітерацій сходиться тоді і тільки тоді, коли  Ця теория предназначена для вирішення задач з двома та бильше невідомими. Висновок: Є багато робіт, де метод Ньютона застосовується до проблем, які не зводяться до рішення рівнянь або оптимізації. прикладами можуть служити завдання додатковості і рівноважні завдання. Існують глибокі результати про складність основних задач обчислювальної математики (таких як відшукання всіх коренів полінома). Багато з них тісно пов'язані з методом Ньютона (Він часто виявляється оптимальним в деякому сенсі методом, придатним для вирішення цих завдань). Швидкість збіжності метода Ньютона досить висока; проте іноді пропонують методи з ще більш високою швидкістю збіжності. Такі спроби не здаються актуальними, тому немає потреби вводити ускладнення для прискорення збіжності. Розділ 2. Проектування програмного продукту Постановка задачі Ціль – реалізація програмного рішення для алгоритму Ньютона-Рафсона з графічним інтерфейсом для вивода графіка похідних и показу наближення точок. Користувач може вільно вписувати довільні функції та працювати з ними. Особливості реалізації Беремо нашу функцію та шукаємо першим її похідну, після цього використовуємо метод Ньютона-Рафсона. Для наших точок ми малюємо графік з довільним кроком, який вибере користувач. Метод полягає в діленні наших вихідних данних на два в кожній ітерації, тобто наша початкова функція поділенна на похідну віднеї. Таким чином ми через цей метод отримаємо перетин чере вісь Ox. Отже з кожною ітерацією ми будемо отримувати все більше наближений графік функції F(x). Узагальнення та варіації методу використовують для обчислення коренів системи нелінійніх рівнянь, знаходження екстремумів функції, обчислення коренів комплексного рівняння. Початкової точки x0 функція F(x0) повинна бути досить мала, тобто точка x0 повинна бути досить близька до вирішення. Таким чином, метод Ньютона сходиться локально. Дуже прості одномірні приклади показують відсутність глобальної збіжності навіть для гладких монотонних F(x). Існують глибокі результати про складність основних задач обчислювальної математики (таких як відшукання всіх коренів полінома). Багато з них тісно пов'язані з методом Ньютона. Для нелінійних рівнянь з двома чи більше невідомими ми будемо вирішувати за допомогою систем нелінійних рівнянь. 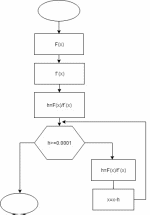 Рисунок 1 – Блок схема алгоритму для нелінійного рівнянння з однією змінною Переваги та недоліки Переваги Алгоритм має властивість зміни точності за рахунок зміни кроків, отже можливо отримувати більш точні значення за рахунок більшої кількості кроків для. Це сприяє тому, що наші данні будуть більш точними. Друга перевага – простота алгоритма для використання. Мала кількість запитів при можливості надання великої кількості кроків. Можна пришвидчити за допомогою графічного метода. Недоліки Є більш швидкі методи сходження в порівнянні з методом Ньютона-Рафсона. Всі результати про збіжність методу Ньютона отримані в припущенні про виконання тих чи інших умов на деякому проміжку. Якщо не існує друга похідна в точці кореня, то швидкість збіжності методу може бути помітно знижена Якщо похідна в точці кореня дорівнює нулю, то швидкість збіжності НЕ буде квадратичної, а сам метод може передчасно припинить пошук, і дасть неправильне для заданої точності наближення. Цей метод неможна використовувати для вирішення нелінійних рівнянь з двома невідомими. Вдосконалення алгоритму 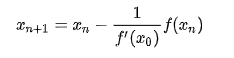 Ця формула дозволяє не обчислювати похідну на кожній ітерації, отже дозволяє позбутися можливого ділення на нуль. Однак цей алгоритм має тільки лінійну збіжність. Іноді, наприклад, поблизу кратного кореня, може відбуватися втрата значущих цифр, що призводить до "розхитування" підрахунку. Це обмежує точність, з якою можна знайти корінь. Від "розхитування" страхуються таким чином (прийом Гарвика) : вибирають не дуже мале Дуже важлива властивість ітераційних методів: помилки округлення в ітераційних методах не накопичуються від ітерації до ітерації. Висновок : Поставлена задача на розробку алгоритму за допомогую середовища розробки. Створити інтерфес для створення графіків, використовуючи бібліотеку «matplotlib». Для повної реалізації нашої умови будуть дотримані всі вище наведені вимоги для створення нашого алгоритму. Розділ 3. Реалізація програмного продукту Код програмного продукту для нелінійного рівняння з однією невідомою import matplotlib.pyplot as plt import numpy as np def func(x): return x * x * x - x * x + 2 def derivFunc(x): return 3 * x * x - 2 * x # Функція пошуку рута def newtonRaphson(x): h = func(x) / derivFunc(x) while abs(h) >= 0.0001: h = func(x) / derivFunc(x) # x (i + 1) = x (i) - f (x) / f '(x) x = x - h print("The value of the root is : ", "%.4f" % x) # Програма драйвера для тестування x0 = -20 # Можливі початкові значення newtonRaphson(x0) X = np.linspace(0, 1000, 1000) Y = [func(x) for x in X] plt.plot(X, Y) plt.show() Головні структури данних Func(x) – наша головна функція; derivFunc(x) – наша похідна функції; newtonRaphson(x) – алгоритм Ньютона-Рафсона; h – кількість кроків(точність); x0 – можливе початкове значення функції; plt.plot(X, Y) – точки за якими буде будуватися наш графік print("The value of the root is : ", "%.4f" % x) – вивід нашого результату Перевірка працездатності программи 1. Функція x^3-x^2+2 2. Кількість кроків 1000 3. Точність 0,0001. 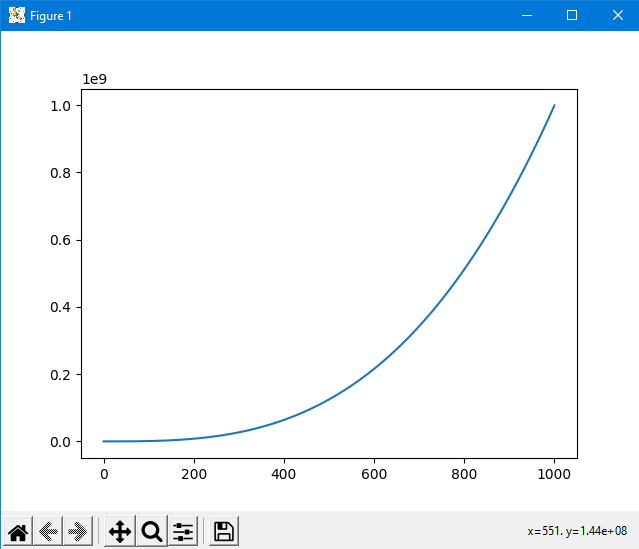 Рисунок 2 – графік функції x^3-x^2+2 при значення наведених вище Рисунок 3 – результат програми 1. Функція 4x^3+8x^2-2; 2. Кількість кроків 1000; 3. Точність 0,0001. 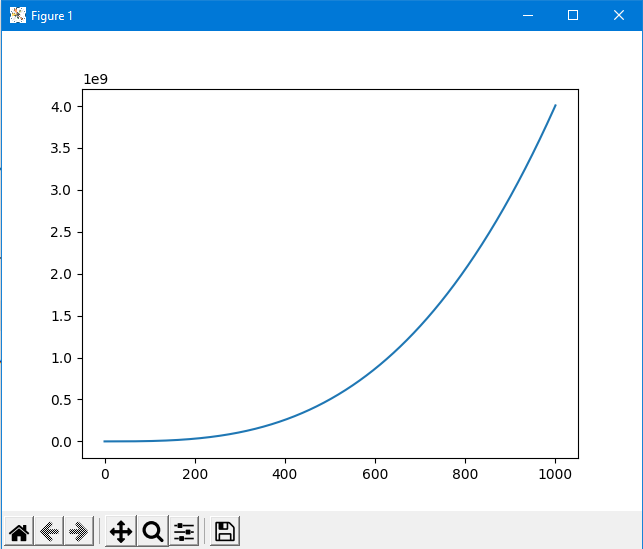 Рисунок 4 – графік функції 4x^3+8x^2-2 при значення наведених вище Рисунок 5 – результат програми Код програмного продукту для нелінійного рівняння з двома невідомими import math import matplotlib.pyplot as plt # Нехай x1 = x, а x2 def f1Function(x,y): return (math.pow(x,2) + 4)*y - 8 # Перша функція def f2Function(x,y): return math.pow(x-1,2)+math.pow(y-1,2) - 4 # Друга функція def jMatrix(x,y): J = [[2*x*y,math.pow(x,2) + 4],[2*x-2,2*y-2]] #Рахуємо часткові похідні для наших двух функцій return J def a1Matrix(x,y): A1 = [[f1Function(x,y),math.pow(x,2) + 4],[f2Function(x,y),2*y -2]] return A1 def a2Matrix(x,y): A2 = [[2*x*y,f1Function(x,y)],[2*x-2,f2Function(x,y)]] return A2 def determine(matrix): return matrix[0][0]*matrix[1][1] - matrix[0][1]*matrix[1][0] #Детермінант квадратної матриці x0 = 10000 #Початкові значення y0 = 0 differnces = [] #Список похибок print("Значення X0 взяте після наближення - " + str(x0)) print("Значення Y0 взяте після наближення - " + str(y0)) print() iter = 1 x1 = x0 - determine(a1Matrix(x0,y0))/determine(jMatrix(x0,y0)) y1 = y0 - determine(a2Matrix(x0,y0))/determine(jMatrix(x0,y0)) print("Значення X1 на " + str(iter) + " ітерації = " + str(x1) + " при значенні X0 - " + str(x0)) print("Значення Y1 на " + str(iter) + " ітерації = " + str(y1) + " при значенні Y0 - " + str(y0)) print("Детермінант матриці А1 - " + str(determine(a1Matrix(x0,y0)))) print("Детермінант матриці А2 - " + str(determine(a2Matrix(x0,y0)))) print("Детермінант матриці J - " + str(determine(jMatrix(x0,y0)))) print() maxDifference = 0 if(math.fabs(x1-x0)>math.fabs(y1-y0)): #Алгоритм який був описан у теорії maxDifference = math.fabs(x1-x0) else: maxDifference = math.fabs(y1-y0) differnces.append(maxDifference) iterations = [iter] while(maxDifference > 0.001): iter += 1 iterations.append(iter) x0 = x1 y0 = y1 x1 = x0 - determine(a1Matrix(x0, y0)) / determine(jMatrix(x0, y0)) y1 = y0 - determine(a2Matrix(x0, y0)) / determine(jMatrix(x0, y0)) print("Значення X1 на " + str(iter) + " ітерації = " + str(x1) + " при значенні X0 - " + str(x0)) print("Значення Y1 на " + str(iter) + " ітерації = " + str(y1) + " при значенні Y0 - " + str(y0)) print("Детермінант матриці А1 - " + str(determine(a1Matrix(x0, y0)))) print("Детермінант матриці А2 - " + str(determine(a2Matrix(x0, y0)))) print("Детермінант матриці J - " + str(determine(jMatrix(x0, y0)))) print() if (math.fabs(x1 - x0) > math.fabs(y1 - y0)): maxDifference = math.fabs(x1 - x0) else: maxDifference = math.fabs(y1 - y0) differnces.append(maxDifference) #Додаємо наші похибок print("Відповідь: значення X - " + str(x1) + ", значення Y - " + str(y1)) print("Кількість ітерацій = " + str(iter)) plt.plot(iterations,differnces) #Вивід графіка ітерацій на екран plt.show() 1. Функції: (x^2+4)*y-8 (x-1)^2+(y-1)^2-4 2. Кількість ітерацій 16 3. Точність 0.001 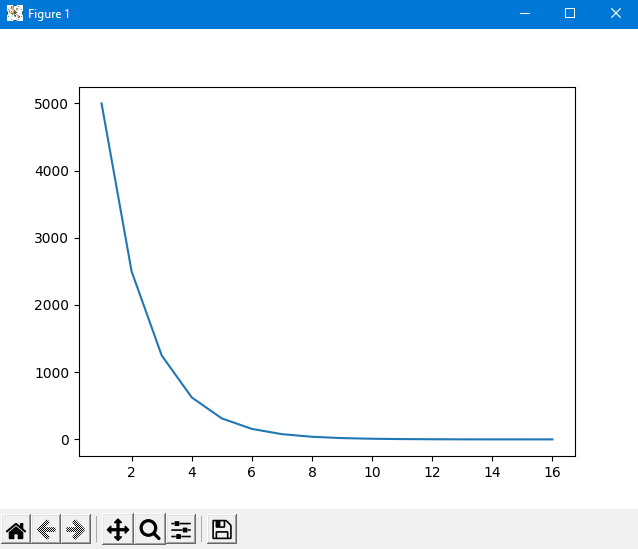 Рисунок 6 – графік ітерацій функцій 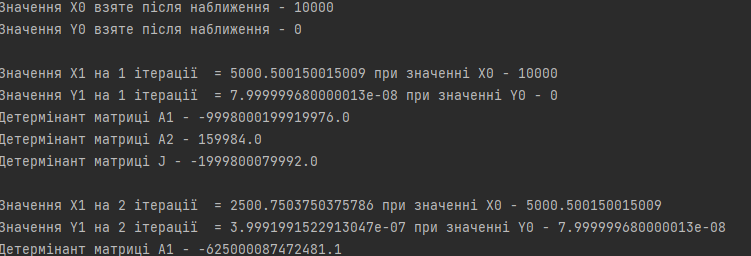 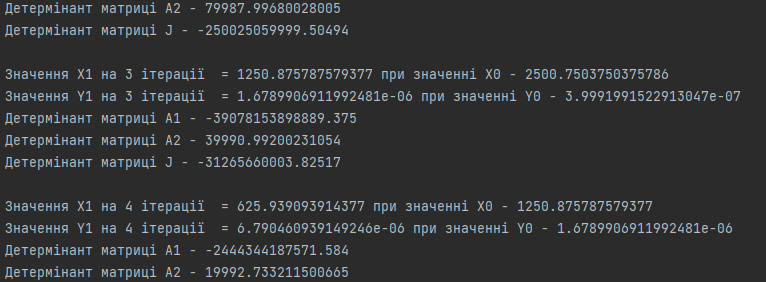 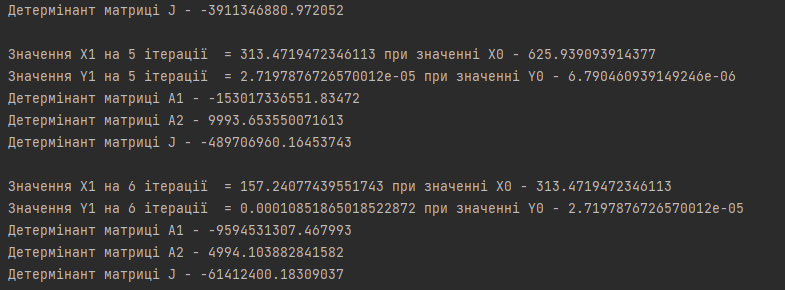 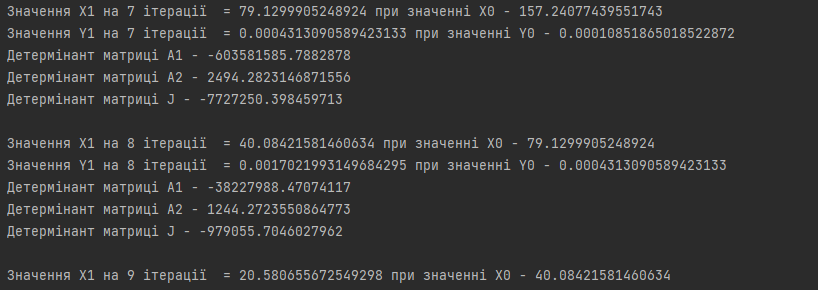 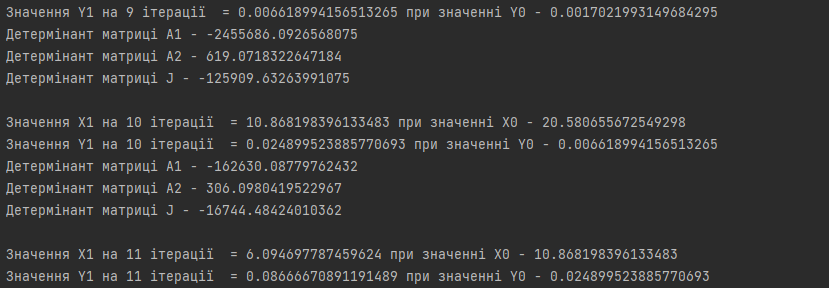 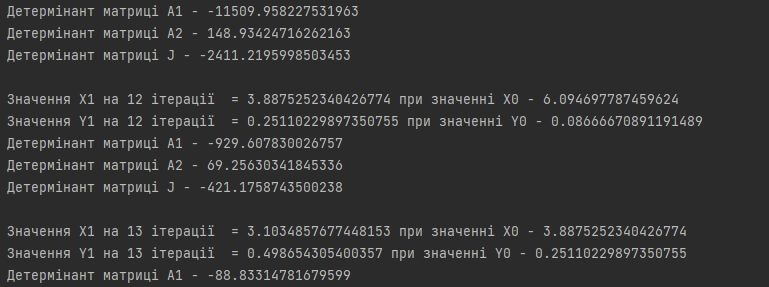 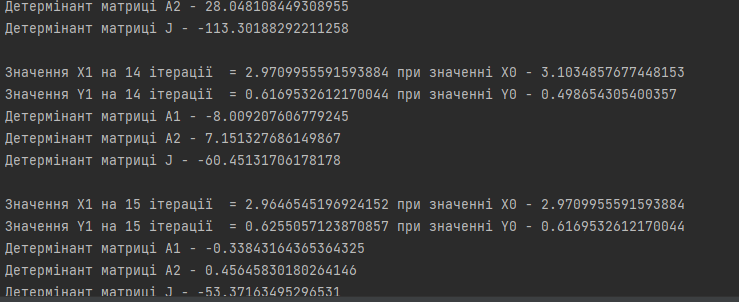 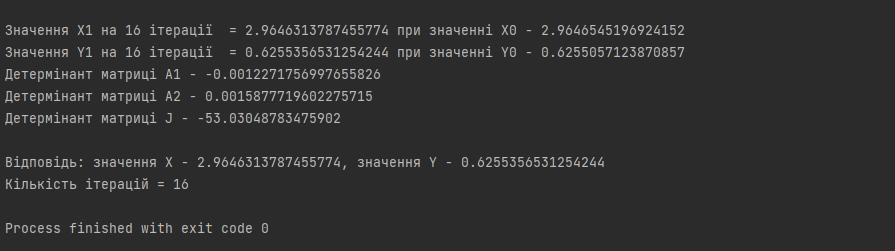 Рисунок 6-14 – результат роботи програми 1. Функції: (x^2+4)*y-8 (x-1)^2+(y-1)^2-4 2. Кількість ітерацій 10 3. Точність 0.001 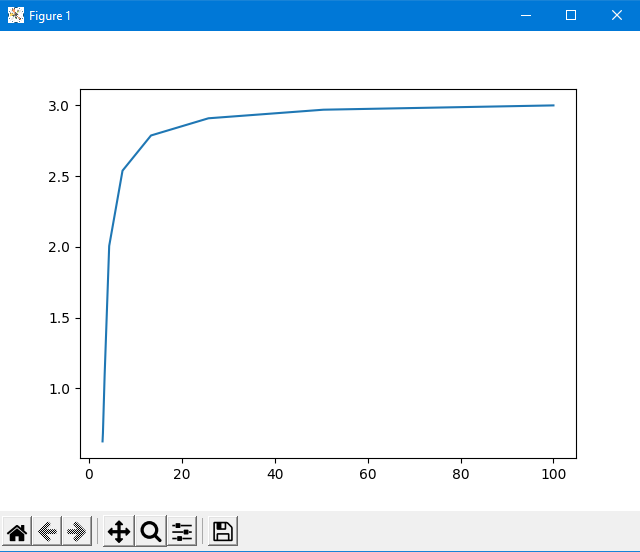 Рисунок 15 – графік, що показує наближення 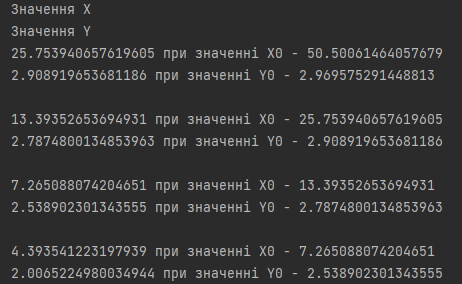   Рисунок 16-19 – результат роботи програми Висновок: При роботі з цим алгоритмом основним недоліком була можливість ділення на нуль, але при оптимізації не виникло таких проблем. Алгоритм дуже швидко показаю наближення та сам по собі є доволі простим при виконанні. Однак у світі є більш швидкі алгоритми з більшою ціною похибки. Однак через його простоту та швидкість виконання він є універсальним рішенням для пошуку наближеного значення функції. Він не потребує багато пам’яті та сам по собі простий. Джерела - Електронні ресурси 1. Алгебраїчні рівняння> Метод Ньютона-Рафсон URL: https://keldysh.ru/pages/comma/html/nonlinear/newton.html 2. Метод дотичних (Ньютона-Рафсона) URL: http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%BA%D0%B0%D1%81%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D1%85_%28%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0-%D0%A0%D0%B0%D1%84%D1%81%D0%BE%D0%BD%D0%B0%29 3. Книга «Метод Ньютона та його роль в оптимізації і обчислювальної математики». Автор Б. Т. Поляк URL: http://www.apmath.spbu.ru/cnsa/pdf/obzor/%D0%9F%D0%BE%D0%BB%D1%8F%D0%BA%20%D0%BE%20%D0%BC%D0%B5%D1%82%D0%BE%D0%B4%D0%B5%20%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0.pdf 4. Метод Ньютона-Рафсона URL: https://matica.org.ua/metodichki-i-knigi-po-matematike/vychislitelnaia-matematika/5-2-1-metod-niutona-rafsona 5. Метод Ньютона-РафсонаURL:https://studme.org/291158/tehnika/metod_nyutona_rafsona6. Метод Ньютона для систем нелінійних рівняньURL:https://algowiki-project.org/ru/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0_%D0%B4%D0%BB%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC_%D0%BD%D0%B5%D0%BB%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D1%8B%D1%85_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B97. Метод Ньютона-РафсонаURL:https://dic.academic.ru/dic.nsf/ruwiki/1034652 |
