Курсавая. Курсавая 1. Методы решения алгебраических и трансцендентных уравнений
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
МИНЕСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «КАЛМЫЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ Б.Б. ГОРОДОВИКОВА» Факультет математики, физики и информационных технологий Кафедра алгебры и анализа КУРСОВАЯ РАБОТА на тему: «Методы решения алгебраических и трансцендентных уравнений» Курсовая работа выполнена студентом (кой) 3 курса направления 02.03.01. Математика и компьютерные науки Саттаров Т.А.__________ Научный руководитель: кандидат физ.-мат. наук, доцент Мучкаева С.С.________ Элиста, 2022 г. Содежание1. Методы решений алгебраических уровненний 1.1 Корни уравнения. Отделение корней 1.2 Численное решение уравнения методом половинного Деления 1.3 Метод Гаусса 1.4 Метод Краута − Дулитла1.5 Метод квадратных корней1.6 Метод прогонки 1.7 Метод простой итерации1.8 Метод Зейделя1.9 Метод релаксации2. Методы решения транцендентных уравненний 2.1 Метод дихотомии2.2 Метод хорд2.3 Метод Ньютона – Рафсона (метод касательных)2.4 Метод наискорейшего спуска2.5 Обобщенный метод Ньютона (поиск комплексных Корней) Веденние Школьник решает системы линейных уравнений путем под- становок (выражает некую переменную из какого-то уравнения, подставляет результат в остальные уравнения и т. д.), переписы- вая имена переменных счетное число раз и допуская счетное ко- личество ошибок. Идея простая, но хаотичная и утомительная в реализации. Самым же популярным среди методов решения ли- нейных систем является метод последовательного исключения переменных – метод Гаусса*, описанный во всех руководствах по численному анализу, реализуемый различными вычислитель- ными схемами, менее утомительный и более изящный по сравне- нию с вышеприведенной реализацией. Иоганн Карл Фридрих Гаусс (1777–1855) − немецкий математик, астро- ном и физик, один из величайших математиков всех времен. С его именем связаны фундаментальные исследования почти во всех основных областях математики. Только за метод наименьших квадратов и нормальный закон распределения (фундамент современной статистики) Гаусса можно назвать «королем математиков». 1.2 Корни уравнения. Отделение корней Функция f(x) называется алгебраической, если для получения ее числового значения по данному значению аргумента хтребуется выполнить арифметические операции и возведение в степень с рациональным показателем. Если в запись уравнения входят только алгебраические функции, то уравне- ние называется алгебраическим. Алгебраическое уравнение всегда может быть приведено к виду anxn an1xn1 an2 xn2 ... a1x a0 0 , (1) где n 1,2,3..., an 0 . Все неалгебраические функции: показательная ах, логарифмическая logax, тригонометрические sin x, cos x, tgx, ctgx и обратные тригонометрические arcsin x, arccos x, arctgx, arcctgx называются трансцендентными. Если в запись уравнения входят трансцендентные функции, то уравнение называется трансцендентным, например tgx ax. Решение уравнения f (x) 0 с одним неизвестным хзаключается в отыска- нии корней, то есть тех значений х, которые обращают уравнение в тождество. В общем случае для уравнения лы, определяющие его корни. f (x) 0 отсутствуют аналитические форму- Задача отыскания корней сводится к нахождению всех точек xiпересечения графика функции f(x) с осью x (см. рисунок 1). Из рисунка видно, что число точек пересечения графика функции с осью x может быть несколько. Поэтому в качест- ве первого шага при решении любого уравнения проводят отделение его корней. Это означает, что ось x разбивают на такие отрезки, что в каждом из них содер- жится только один корень уравнения. После этого следует уточнить положение каждого корня в пределах допустимой погрешности. 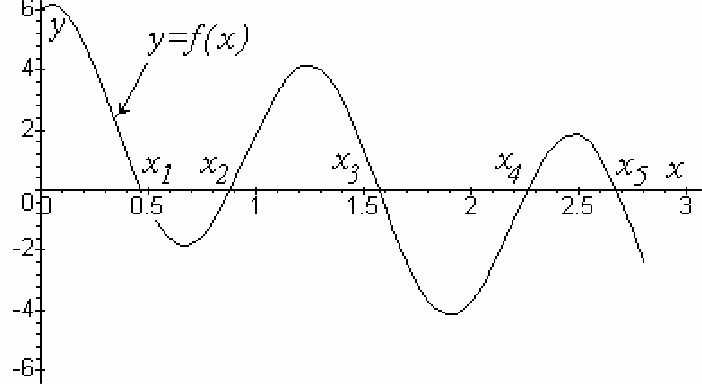 Для отделения корней полезна следующая теорема: если непрерывная функ- ция f(x) принимает значения разных знаков на концах отрезка [a,b] , т.е. f(a) f(b) 0 , то внутри этого отрезка содержится, по меньшей мере, один ко- рень уравнения f(x) = 0. На основе этой же теоремы реализуются самые простые и надежные методы численного определения корней уравнений: метод половинного деления и метод хорд. Процесс отделения корней начинается с установления знаков f(x) в гранич- ных точках интересующего нас отрезка определения переменной x: x = a и x = b. Затем определяются знаки f(x) в ряде промежуточных точек x = 1, 2 ..., выбор которых должен учитывать особенности функции f(x).Если окажется, что f(i)f(i+1) < 0, то в интервале (i, i+1) есть корень уравнения f(x) = 0. Необходимо убедиться, является ли этот корень единственным на данном интервале. Для отделения корней практически достаточно провести процесс половинного деле- ния, последовательно деля исходный отрезок [a, b] на 2, 4, 8 и т. д. равных частей и определяя знаки f(x) в точках деления. Напомним, что алгебраическое уравнение (1) степени n имеет не более n действительных корней. Поэтому если для алгеб- раического уравнения мы получили n+1 перемену знака f(x), то все его корни от- делены. Пример1.Отделить корни уравнения x3 6x+2 = 0. Имеем f(x) = x3 6x+2. Составим приблизительную таблицу перемены знака f(x):
Из данных, приведенных в таблице, следует, что в интервалах (−3, −1); (0, 1) и (1, 3) происходит перемена знака f(x) . Так как f(x) – полином 3-й степени, то все корни в заданном уравнении отделены. Пример2.Отделить корни уравнения х4 4х 1 0 . В данном примере f(x) х4 4х 1, f'(x) 4х3 4 4x3 1, поэтому f'(x) 0 при x 1 это точка экстремума функции f(x) . Далее имеем: f() 0 , f(1) 0 , f() 0 . Следовательно, точка x 1 является точкой минимума, а рас- сматриваемое уравнение имеет только два действительных корня, один из кото- рых лежит в интервале (,1) , а другой – в интервале (1, ) . 1.2 Численное решение уравнения методом половинного деления |
