Курсавая. Курсавая 1. Методы решения алгебраических и трансцендентных уравнений

• Название: Методы решения алгебраических и трансцендентных уравнений
• Анкор: Курсавая
• Дата: 22.06.2022
• Размер: 0.64 Mb.
• Имя файла: Курсавая 1.docx
• Тип: Курсовая; #610528
• страница: 9 из 9

2.4 Метод наискорейшего спуска

Популярный в приложениях метод наискорейшего спускадля случая одной переменной упрощается до элементарнейшего алгоритма.

Выбираем приближение к корню X_nи начальный шаг H. Ес- ли f (X_n) > 0, производим переход в точку X_n+1 слева или справа от X_nв зависимости от знака f′(X_n) (в сторону убывания функции):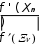

X_n+1 = X_n− H.
Если f (X_n+1) < f (X_n), то эта точка принимается за очередное при- ближение и процесс продолжается; в противном случае возвра- щаемся в точку X_n, уменьшаем шаг вдвое и повторяем переход. Процесс продолжается до малого шага или малого значения функции (его сходимость зависит от близости начального при- ближения к корню и удачного выбора шага).

Очевидно, что такой метод приемлем и в случае кратных корней.

2.5 Обобщенный метод Ньютона (поиск комплексных корней)

Этот метод является, как нам кажется, самым эффективным методом поиска любых корней уравнения и, в частности, всех корней алгебраического многочлена [1].

Возьмем уравнение f (Z) = 0, выберем начальное приближе- ние к корню Z_k= X_k+ i Y_kи начальный шаг t (например, t = 1).Находим первую отличную от нуля производную f ^(m)(Z_k) и после- дующий процесс приближений ведем по формуле



1

^Zk1 ^{ Z}k



 t^



f(Z_k) ^m

f^(m) (Z_k) _

.

Если f (Z_k+1) > f (Z_k), то tуменьшаем вдвое (как в методе наискорейшего спуска) и повторяем переход до f (Z_k) <  или близости очередных приближений.

В случае, когда f (Z) является алгебраическим многочленом (полиномом), метод сходится при любом начальном приближе-

нии к одному из корней. Для аналогичного поиска других корней полинома достаточно его степень понизить делением на (Z − Z*), где Z* − найденный корень.

Для примера найдем корни алгебраического уравнения P (Z) = Z³ − 5 Z² + 9 Z − 5 = 0. Пусть t = 1 и начальное приближе- ние Z₀ = 0. Отыскав первую производную P(Z) = 3 Z² − 10 Z+ 9


⁰  01 


и обнаружив P(Z₀) = 9 ≠ 0, ищем первое приближение (m= 1):

Z Z

1 0



1^



P(Z) _



P^(Z₀ ) _

^{ 5}  0.556 .

9

Значение полинома уменьшилось, т. к.

P(Z₁)  –1.37 < P(Z₀) = 5, продолжаем итерации:

Z  Z

³ 2

1



P(Z)

2
^1 P^(Z
^  1.004 1 





)
 1.000 .


0.008


2

 2 

В итоге обнаруживаем, что Z = 1 − один из корней уравне- ния. Разделив P(Z) на Z − 1, получаем уравнение P₂(Z) = Z² − 4 Z + 5 = 0 с производной P₂(Z) = 2 Z − 4. Вновь возьмем t = 1 и начальное приближение Z₀ = 0. Аналогично предыдущему рассмотрению, имеем:

P₂(Z₀) = 5; P₂(Z₀) = 2  0 − 4 = −4; Z₁ = 0 + 1  5 / 4 = 1.25;

P₂(Z₁) = 1.5625; P₂(Z₁) = −1.5; Z₂ = 1.25 + 1  1.5625 / 1.5  2.2916;

P₂(Z₂) = 1.0851; P₂(Z₂) = 0.5833; Z₃ = 2.2916 − 1  1.0851 / 0.5833 

0.4315;

P₂(Z₃) = 3.4600; (значение полинома > P₂(Z₂) = 1.0851 − уменьша- ем tдо 0.5); Z₄ = 2.2916 − 0.5  1.0851 / 0.5833  1.3616;

P₂(Z₄) = 1.4075; (значение полинома > P₂(Z₂) = 1.0851 − уменьша- ем tдо 0.25); Z₅ = 2.2916 − 0.25  1.0851 / 0.5833  1.8266;

P₂(Z₅) = 1.0301; P₂(Z₅) = −0.3467;

Z₆ = 1.8266 + 0.25  1.0301 / 0.3467  2.5693;

P₂(Z₆) = 1.3241; (значение полинома > P₂(Z₅) = 1.0301; следова- тельно, уменьшаем tдо 0.125 и т. д.).

После серии переходов с многократным изменением t полу- чается оценка Z₂₀ = 2.0000 со значениями P₂(Z₂₀) = 1; P₂(Z₂₀) = 0. Поскольку значение производной обратилось в нуль, берем m = 2, находим ненулевую P₂(Z₂₀) = 2 и получаем (восстановив t= 1)

1

^ P(Z

_{) }² _1

Z  Z

_1^_2 20 ^

 2.0000 1  ^{1.00 2}

 2.0000 ¹ i.

)
21 20

 _P''(Z  ₂





2 20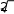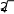

Здесь P₂(Z₂₁) = 0.5; P₂(Z₂₁) = i/ ;

Z₂₂ = (2.0000 + i/

) − 0.5 / (i/

) = 2 + i ;

P₂(Z₂₂) = 3 > P₂(Z₂₁) (вновь уменьшаем tдо 0.5 и т. д. до получения оценки, близкой к истинному корню Z = 2 + i. В силу веществен- ности коэффициентов уравнения третий из корней является ком- плексно-сопряженным Z= 2 − i.

Литература

1. 
   Математический практикум / Г. Н. Положий, Н. А. Пахарева, И. З. Степаненко, П. С. Бондаренко, И. М. Великоиваненко ; под ред. Г. Н. Положего. − Москва : Физматгиз, 1960. – 512 с.
   
2. 
   Березин, И. С. Методы вычислений (в 2-х томах). Т. 2 / И. С. Березин, Н. П. Жидков. − Москва : Физматгиз, 1962. – 620 с.
   
3. 
   Крылов, А. Н. Лекции о приближенных вычислениях. − Москва : Гостехиздат, 1954. – 400 с.
   
4. 
   Демидович, Б. П. Основы вычислительной математики / Б. П. Демидович, И. А. Марон. − Москва : Наука, 1966. – 664 c.
   
5. 
   Хаусхолдер, А. С. Основы численного анализа. − Москва : Издательство иностранной литературы, 1956. – 321 с.
   
6. 
   Фаддеев, Д. К. Вычислительные методы линейной алгеб- ры / Д. К. Фаддеев, В. Н. Фаддеева. − Москва : Физматгиз, 1963. – 734 с.
   
7. 
   Воеводин, В. В. Численные методы алгебры (теория и ал- горифмы). − Москва : Наука, 1966. – 243 с.
   
8. 
   Форсайт, Дж. Численное решение систем линейных ал- гебраических уравнений / Дж. Форсайт, К. Молер. − Москва : Мир, 1969. – 168 с.
   
9. 
   Ланцош, К. Практические методы прикладного анализа. Справочное руководство. − Москва : Физматгиз, 1961. – 524 с.
   
10. 
    Ланс, Дж. Н. Численные методы для быстродействую- щих вычислительных машин. − Москва : Издательство иностран- ной литературы, 1962. – 208 с.
    
11. 
    Демидович, Б. П. Численные методы анализа: приближе- ние функций, дифференциальные и интегральные уравнения / Б. П. Демидович, И. А. Марон, Э. З. Шувалова. − Mосква : Наука, 1967. – 368 c.
    
12. 
    Копченова, Н. В. Вычислительная математика в приме- рах и задачах / Н. В. Копченова, И. А. Марон. − Москва : Наука, 1972. – 368 с.
    
13. 
    Агеев, М. И. Библиотека алгоритмов 151б-200б: Спра- вочное пособие. Вып. 4 / М. И. Агеев, В. П. Алик, Ю. И. Марков ;
    

14. 
    Программное обеспечение ЭВМ МИР-1 и МИР-2. Чис- ленные методы. Т. 1. − Киев : Наукова думка, 1976. – 280 с.
    
15. 
    Программное обеспечение ЭВМ МИР-1 и МИР-2. Про- граммы. Т. 2. − Киев : Наукова думка, 1976. – 371 с.
    
16. 
    Загускин, В. Л. Справочник по численным методам ре- шения алгебраических и трансцендентных уравнений. − Москва : Физматгиз, 1960. – 216 с.
    
17. 
    Воробьева, Г. Н. Практикум по вычислительной матема- тике / Г. Н. Воробьева, А. Н. Данилова. − Москва : Высшая шко- ла, 1990. – 208 с.
    
18. 
    Бусленко, Н. П. Метод статистических испытаний (Мон- те-Карло) и его реализация на цифровых вычислительных маши- нах / Н. П. Бусленко, Ю. А. Шрейдер. − Москва : Физматгиз, 1961. – 228 с.
    
19. 
    Годунов, С. К. Разностные схемы. Введение в теорию / С. К. Годунов, В. С. Рябенький. − Москва : Наука, 1977. – 440 с.
    
20. 
    Яненко, Н. Н. Метод дробных шагов решения многомер- ных задач математической физики. − Новосибирск : Наука, 1967.
    

– 197 с.

21. 
    Хемминг, Р. В. Численные методы для научных работни- ков и инженеров. − Москва : Наука, 1972. – 400 с.
    
22. 
    Марчук, Г. И. Методы вычислительной математики. – Москва : Наука, 1977. – 456 с.
    
23. 
    Тихонов, А. Н. Вводные лекции по прикладной матема- тике / А. Н.Тихонов, Д. П. Костомаров. − Москва : Наука, 1984. – 192 с.
    
24. 
    Мак-Кракен, Д. Численные методы и программирование на Фортране / Д. Мак-Кракен, У. Дорн. − Москва : Мир, 1977. – 583 с.
    
25. 
    Самарский, А. А. Численные методы / А. А. Самарский, А. В. Гулин. − Москва : Наука, 1989. – 432 с.
    
26. 
    Корн, Г. Справочник по математике для научных работ- ников и инженеров / Г. Корн, Т. Корн. − Москва : Наука, 1984. – 832 с.
    
27. 
    Беккенбах, Э. Ф. Современная математика для инжене- ров. − Mосква : Издательство иностранной литературы, 1958. – 498 с.
    
28. 
    Янке, Е. Специальные функции (формулы, графики, таб- лицы) / Е. Янке, Ф. Эмде, Ф. Леш. − Mосква : Наука, 1964. – 344 с.
    
29. 
    Банди, Б. Методы оптимизации (вводный курс). − Москва : Радио и связь, 1988. – 128 с.
    

Литература последних лет

30. 
    Демидович, Б. П. Основы вычислительной математики / Б. П. Демидович, И. А. Марон. – Санкт-Петербург : Лань, 2011. – 672 с.
    
31. 
    Демидович, Б. П. Численные методы анализа. Прибли- жение функций, дифференциальные и интегральные уравнения / Б. П. Демидович, И. А. Марон, Э. З. Шувалова. – Санкт- Петербург : Лань, 2010. – 400 с.
    
32. 
    Копченова, Н. В. Вычислительная математика в приме- рах и задачах / Н. В. Копченова, И. А. Марон. – Санкт- Петербург : Лань, 2009. – 368 с.
    
33. 
    Берцун, В. Н. Сплайны сеточных функций. – Томск : Изд-во Томск. гос. ун-та, 2002. – 124 с.
    
34. 
    Меркулова, Н. Н. Методы приближенных вычислений : учеб. пособие / Н. Н. Меркулова, М. Д. Михайлов. – Томск : Изд- во Томск. гос. ун-та, 2011. – 184 с.
    
35. 
    Самарский, А. А. Введение в численные методы : учеб. пособие для вузов. − Санкт-Петербург : Лань, 2005. – 288 с.
    
36. 
    Бахвалов, Н. С. Численные методы в задачах и упражне- ниях : учеб. пособие / Н. С. Бахвалов, А. В. Лапин, Е. В. Чижон- ков. − Москва : Высшая школа, 2000. – 190 с.
    
37. 
    Бахвалов, Н. С. Численные методы / Н. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков. − Москва : БИНОМ. Лаборатория знаний, 2009. – 632 с.
    
38. 
    Чен, К. MATLAB в математических исследованиях / К. Чен, П. Джиблин, А. Ирвинг. – Москва : Мир, 2001. – 346 с.
    
39. 
    Мэтьюз, Д. Г. Численные методы. Использование MATLAB / Д. Г. Мэтьюз, К. Д. Финк. − Москва : Вильямс, 2001. – 720 с.
    

41. 
    Плис, А. И. MATHCAD 2000. Математический практи- кум / А. И. Плис, Н. А. Сливина. – Mосква : Финансы и статисти- ка, 2000. – 656 с.
    
42. 
    Иглин, С. П. Математические расчеты на базе MATLAB.
    

– Санкт-Петербург : БХВ – Петербург, 2005. – 640 с.

41. 
    Потемкин, В. Г. Система инженерных и научных расче- тов MATLAB 5.x. Т. 1. – Mосква : Диалог-МИФИ, 1999. – 366 с.
    
42. 
    Воеводин, В. В. Параллельные вычисления / В. В. Воево- дин, Вл. В. Воеводин. − Санкт-Петербург : БХВ − Петербург, 2002. – 608 с.
    
43. 
    Старченко, А. Б. Параллельные вычисления на много- процессорных вычислительных системах / А. Б. Старченко, А. О. Есаулов. – Томск : Изд-во Томск. гос. ун-та, 2002. – 56 с.
    
44. 
    Афанасьев, К. Е. Многопроцессорные вычислительные системы и параллельное программирование / К. Е. Афанасьев, С. В. Стуколов. – Кемерово : Кузбассвузиздат, 2003. – 233 с.
    
45. 
    Недорезов, Л. В. Введение в экологическое моделирова- ние : учеб. пособие. Т. 1. – Новосибирск : Изд-во Новосиб. гос. ун-та, 1998. – 142 с.
    
46. 
    Недорезов, Л. В. Введение в экологическое моделирова- ние : учеб. пособие. Т. 2. – Новосибирск : Изд-во Новосиб. гос. ун-та, 1999.