Курсавая. Курсавая 1. Методы решения алгебраических и трансцендентных уравнений
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
1.5 Метод квадратных корнейВ многочисленных приложениях (в частности, при обработ- ке статистических данных) возникает система уравнений с сим- метрической матрицей коэффициентов (матрица Аназывается симметрической, если для ее элементов выполняется условие аij= аjiпри всех i и j). Такие матрицы представляют частный слу- чай так называемых эрмитовых матриц*, в которых элементы главной диагонали вещественны, а симметричные образуют пары комплексно сопряженных чисел. Например: 1 8   8 3 2 i 0 11 i . 2 i 11 7 1     9 0 i 1 Всякую вещественную симметрическую матрицу можно предста- вить произведением взаимно транспонированных матриц A= RT R, где r11 0 R ... r12 r22 ... ... ... ... r1n  r2n . ... 0 0 ... r nn Перемножая матрицы, получаем систему r2 r2 … r2 a ; i, j 1, 2,…, n; 1i 2i ii ii r1ir1 j r2ir2 j … riirij aij , i 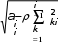 решение которой имеет вид решение которой имеет видrii , i 1, 2,…, n; r 1 a i1 r r , j i 1, i 2,…, n. ij r ij ki kj ii k1 Полученное разложение сводит систему AX= Bк двум си- стемам с треугольными матрицами коэффициентов RT Y = B, R X = Y, решаемым по схеме, описанной выше для метода Краута. Если матрица А− положительно определенная (все ее глав- ные миноры положительны), все элементы матрицы R − веще- ственные числа. В общем случае элементы R могут быть и чисто мнимыми числами. Самый плохой случай в технологии такого разложения возникает, когда какие-то из главных миноров обра- щаются в нуль. Метод квадратных корней является самым быстродейству- ющим, но его программная реализация требует операций с повы- шенной точностью (точность теряется из-за операций извлечения корня) и арифметики комплексных чисел. Рассмотрим пример применения метода квадратных корней.
Получаем r 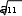 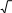 1 1, r 1 1, r a12 2 2 , r a13 3 3, 11 r22   12 a22 r2 12 r11  1 13 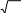 1 i, 1 i,r11 1 r23 1 a23 r12r13 1 4 2 3 2 / i 2 i, i i  r33 r33 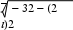 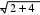 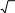 2. 2.То есть
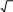 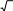 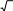 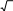  Согласно методу Краута, получаем Согласно методу Краута, получаем
|
