Курсавая. Курсавая 1. Методы решения алгебраических и трансцендентных уравнений
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
| b1 | c1 | 0 | 0 | 0 | … | 0 | 0 | | x1 | | d1 |
| a2 | b2 | c2 | 0 | 0 | … | 0 | 0 | | x2 | | d2 |
| 0 | a3 | b3 | c3 | 0 | … | 0 | 0 | | x3 | | d3 |
| 0 | 0 | a4 | b4 | c4 | …. | 0 | 0 | | x4 | = | d4 |
| 0 | 0 | 0 | ak | bk | … | 0 | 0 | | x5 | | d5 |
| … | … | … | … | … | … | … | … | | | | |
| 0 | 0 | 0 | 0 | 0 | | an | bn | | xn | | dn |
или в компактном виде
b1 x1 + c1 x2 = d1,
akxk-1 + bkxk+ ckxk+1 = dk, k= 2, ..., n – 1,
anxn-1 + bn xn= dn.
Положим
xk= Pkxk+1 + Qk, k= 1, 2, …, n – 1
и, подставив в получим
или
ak(Pk–1 xk+ Qk–1) + bkxk+ ckxk+1 = dk, k= 2, 3, …, n – 1
(akPk–1 + bk) xk+ ckxk+1 = dk− akQk–1, k= 2, 3, …, n – 1.
С учетом представления первого уравнения в виде
x2 = (d1 − b1 x1) / c1
и последнего:
an(Pn–1 xn+ Qn–1) + bnxn= dn,
получаем двухшаговую процедуру решения: на прямомходе ищем прогоночные коэффициенты в порядке роста k и на обратном– находим решение системы:
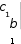 P
P 1
P
, Q
1
ck
,
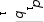 , Q dk
, Q dkakQk1 , k
2,…, n 1;
k bk
akPk1
k bk
akPk1
x dn anQn1 , x
Px Q, k
n 1, n 2,…,1.
n bn anPn1 k
kk1 k
Заметим, что трехдиагональная матрица коэффициентов со- держит только 3 n – 2 << n2 ненулевых элементов, что при раз- мерности порядка сотен существенно сокращает требования к объему используемой памяти компьютера. Этот метод называ- ют методомпрогонки; его использование значимо уменьшает объем вычислительных затрат в сравнении с любыми другими методами.
Существуют видоизменения метода прогонки для систем с более чем трехдиагональной матрицей коэффициентов (в частности, пятидиагональных), но здесь приходится обра- щать матрицы.

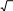
 1.6 Метод
1.6 Метод