Курсавая. Курсавая 1. Методы решения алгебраических и трансцендентных уравнений

• Название: Методы решения алгебраических и трансцендентных уравнений
• Анкор: Курсавая
• Дата: 22.06.2022
• Размер: 0.64 Mb.
• Имя файла: Курсавая 1.docx
• Тип: Курсовая; #610528
• страница: 8 из 9

)  ¹

2

f(Z_n)

f'(Z_n)

f' ' (Z_n

)^ 

_

 f(Z

_{)  1 h}2[ f'(Z_n)]²  f(Z_n) f''Z_n)] _{ 0.}

n  

_ f'(Z_n) _


2
Откуда получаем формулу

h 

2 f(Z_n) f'(Z_n) _

2[ f'(Z_n)]²  f(Z_n)  f''(Z_n)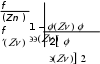
.

Для уточнения корня можно воспользоваться методом Эй-ткена – Стеффенсена, который строится как сочетание методов хорд и простой итерации с итерационным процессом вида

Можно свести решение системы линейных уравнений

n

^{ a}ij^xj

j1

 b_i,

i 1, n

к задаче минимизации (до нуля) функции

n _ n

_2

_ g_i^ _ a_ijx_j b_i^

, g_i

• 
  0, i 1, n.
  

i1 _ j1 _

В самом деле, если решение (2.32) существует и оно един- ственно, то (2.33) обращается в нуль. В случае противоречивой системы достижение нуля нереально, и существенную роль игра- ет выбор весовых коэффициентов g_i, выражающих степень зна- чимости соблюдения того или иного уравнения (2.32). Очевидно, что решение задачи оптимизации не проще использования других рассмотренных здесь методов, требует знакомства с соответ- ствующими методами оптимизации и, может быть, даже с мето- дами случайных испытаний (методами Монте-Карло).

Мы не пытаемся рассмотреть все многообразие прямых и итерационных методов решения линейных алгебраических си- стем, большинство из которых потеряло свою практическую зна- чимость в век могущества вычислительной техники. Заметим только, что для систем высокого порядка, где матрица коэффици- ентов может быть разбита на блоки, среди которых есть нулевые, используют клеточные методы, сводящие исходную задачу к по- следовательному перебору клеток (блоков) матрицы и поиску со- ответствующих обратных матриц.

Особого внимания заслуживают и «плохообусловленные» системы, для которых определитель матрицы близок к нулю. Здесь малейшее изменение исходных данных ведет к значитель- ному изменению решения (решение неустойчиво по исходным
данным). В принципе может обнаружиться и отсутствие решения

− несовместность системы. Разрешение такой ситуации, связан- ной обычно с некорректной постановкой задачи, предлагает ме-тод регуляризации А. Н. Тихонова^*, сводящий исходную систему AX= Bк всегда совместной системе

(A^TA+  E) X= A^TB,  > 0,

где параметр  выбирается с учетом требуемой точности решения и погрешности исходных данных.

К решению системы A^TA X = A^TB сводится и случай пере-определенных систем, в которых число уравнений m превышает число переменных n (m> n)