Курсавая. Курсавая 1. Методы решения алгебраических и трансцендентных уравнений
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
1.7 Метод простой итерацииИдея итерационных методов решения системы уравнений AX= Bсостоит в преобразовании ее к виду X= X+ с последующим использованием сходящегося итерационного процесса X(k+1) = X(k) + , k= 0, 1, 2, …, где начальное приближение X(0) выбирается произвольно, напри- мер, равным нулю или оценкам, найденным другими методами. Процесс итераций заканчивается обнаружением близости очеред- ных приближений. Прежде чем говорить об условиях сходимости итерационно- го процесса (2.19), напомним понятие нормы матрицы. Нормойэлемента Uназывают скалярную величину ||U||, обладающую свойствами: ||U|| 0 при всех U, причем ||U|| = 0 при U= 0; 2) ||k U|| = k ||U||, где k– скаляр; 3) ||U+ V|| ||U|| + ||V||. С этим понятием мы встречаемся в курсе школьной математики при знакомстве с длиной вектора, заявляя, что в треугольнике длина любой стороны меньше суммы длин двух других его сто- рон. За норму скаляра принимается его абсолютная величина. 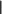 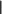 В качестве нормы вектора приемлемы варианты В качестве нормы вектора приемлемы варианты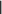 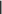 X1 xi, X1 xi,i X x2 , 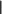 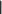   i 2 i Xinf max xi i . За норму матрицы выбирают из нескольких вариантов: 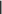 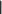 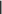 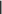 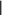 A max aij, A max aij, A A max aij, A max aij, A 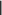 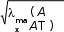   j i 1 inf 2 i j (здесь max – максимальное собственное число матрицы ААТ; о поиске собственных чисел см. ниже) или завышенную евклидо- ву норму 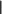 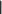 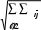 A . A . Достаточным условием сходимости итерационного процес- са является весьма жесткое требование: |||| K< 1. Выполнение этого условия легко обеспечивается, если вне- диагональные элементы матрицы A по модулю много меньше со- ответствующих диагональных элементов |аij| << |аii|, например, при всех i n а аii. j1 ijii В общем случае сведение A X = B к виду X = X + с со- блюдением условия |||| K < 1 неоднозначно и требует опреде- ленного искусства. Пример 1. Возьмем такую систему [4]: 4 x1 + 0.24 x2 − 0.08 x3 = 8, 0.09 x1 + 3 x2 − 0.15 x3 = 9, 0.04 x1 − 0.08 x2 + 4 x3 = 20 и элементарным делением на диагональные элементы преобразу- ем ее к эквивалентной системе x1 = 2 − 0.06 x2 + 0.02 x3, x2 = 3 − 0.03 x1 + 0.05 x3, x3 = 5 − 0.01 x1 + 0.02 x2. При нулевом начальном приближении получаем
(здесь сходимость процесса очевидна; уже найденное четвертое приближение гарантирует, по крайней мере, четыре верных зна- чащих цифры). Заметим, что соблюдения условия |||| K < 1 достаточно для сходимости, но не всегда в этом есть необходимость. Пусть исходная система приведена к виду x1 = 1.5 + 0.5 x1 − x2, x2 = 1.1 + 0.5 x1 − 0.6 x2. 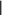 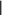 Приведенные в (2.22) оценки нормы матрицы коэффициен- Приведенные в (2.22) оценки нормы матрицы коэффициен-тов A=1.6, 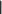 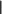 1 1A=1.1, 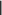 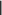 inf infA2 = 1.84 (последнюю из них обсудим позднее) превышают 1. Тем не менее процесс итераций оказывается сходящимся
Условие |аij| <<|аii| эффективного преобразования А X = Bк виду X = X + делением на диагональные элементы можно ослабить, если диагональные элементы близки к 1, а внедиаго- нальные достаточно малы. Пример 2. Возьмем систему 1.12 x1 + 0.24 x2 − 0.08 x3 = 8, 0.09 x1 + 0.95 x2 − 0.15 x3 = 9, 0.04 x1 − 0.08 x2 + 1.53 x3 = 20 и преобразуем ее к виду x1 = 8 − 0.12 x1 − 0.24 x2 + 0.08 x3, x2 = 9 − 0.09 x1 + 0.05 x2 + 0.15 x3, x3 = 20 −0.04 x1 − 0.08 x2 − 0.53 x3. Очевидно, что норма матрицы
меньше 1 и процесс простой итерации сходится
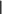 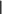 Процесс итераций заканчивается обнаружением близости очередных приближений в смысле абсолютной или относитель- ной погрешности [12, с. 78]: Процесс итераций заканчивается обнаружением близости очередных приближений в смысле абсолютной или относитель- ной погрешности [12, с. 78]:x(k1) xk , x(k1) xk , max i i i max i i i 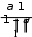 max maxx(k1) xk x(k1) . i i i i |
