Курсавая. Курсавая 1. Методы решения алгебраических и трансцендентных уравнений

• Название: Методы решения алгебраических и трансцендентных уравнений
• Анкор: Курсавая
• Дата: 22.06.2022
• Размер: 0.64 Mb.
• Имя файла: Курсавая 1.docx
• Тип: Курсовая; #610528
• страница: 7 из 9

1.8 Метод Зейделя

Процесс простой итерации в развернутом виде

n

_x(k1)

 _

x^(k)   ,

i 1, 2, ..., n.

i ij j ij1

Метод Зейделя отличается тем, что на очередной итерации берут не оценки предыдущей итерации, а последние полученные:

x
(k 1) 1

n

 __ijj1

x^(k)   ,

j 1

1

j 2
n

x


(k 1) 2

_21x(k) _

^2 j

j2

x^(k)   ,

_x(k1)

i1

 _

n

_x(k1) _{ }

x^(k)   .

i ij j

j1

ji

ij j i

Так для приведенной выше системы

x₁ = 2 − 0.06 x₂ + 0.02 x₃,

x₂ = 3 − 0.03 x₁ + 0.05 x₃,

x₃ = 5 − 0.01 x₁ + 0.02 x₂.

при нулевом начальном приближении получаем


1
x⁽¹⁾ = 2,


2
x⁽¹⁾ = 3 − 0.03 ∙ 2 = 2.94,


3
x⁽¹⁾ = 5 − 0.01 ∙ 2 + 0.02 ∙ 2.94 = 5.0388,


1
x⁽²⁾ = 2 − 0.06 ∙ 2.94 + 0.02 ∙ 5.0388 = 1.9244, …

Как правило, метод Зейделя ускоряет сходимость прибли- жений к истинному решению.

1.9 Метод релаксации

Среди итерационных методов достаточно популярен методрелаксации (ослабления) [2], где на каждом шаге меняется значе- ние только одной из компонент вектора приближения. Здесь ис- ходную систему A X = B (например, делением на диагональные элементы) преобразуем к эквивалентному виду

–x₁ + c₁₂ x₂ +… + c_1nx_n+ d₁ = 0,

c₂₁ x₁ – x₂ + … + c_2nx_n+ d₂ = 0,

. . . .. . .. . . .. . .. . . .. . .. . . .. . .. . .. . . ... . ..

c_n1 x₁ + c_n2 x₂ + … – x_n+ d_n= 0

и подстановкой начального приближения X⁽⁰⁾ в получаем так называемые «невязки»:

R₁⁽⁰⁾ = d₁ − x₁⁽⁰⁾ + c₁₂ x₂⁽⁰⁾ + … + c_1nx_n⁽⁰⁾,

R₂⁽⁰⁾ = d₂ – x₂⁽⁰⁾ + c₂₁ x₁⁽⁰⁾ + … + c_2nx_n⁽⁰⁾,

. . . .. . .. . . .. . .. . . .. . .. . . .. . .. . .. . . ... . ..

R_n⁽⁰⁾ = d_n− x_n⁽⁰⁾ + c_n1 x₁⁽⁰⁾ + … + c_{n n–1} x_n–1⁽⁰⁾

или в компактной форме


i i i
_R(0) _{= d− x}(0) ₊

^cij

ji
_x(0) _,
i 1, 2,…, n.

j
Выберем максимальную по модулю невязку R_s⁽⁰⁾ и положим в очередном приближении

x_s⁽¹⁾ = x_s⁽⁰⁾ + R_s⁽⁰⁾

(подавляя эту невязку). Корректируя остальные невязки, имеем

R_s⁽¹⁾ = 0, R_i⁽¹⁾ = R_i⁽⁰⁾ + c_is R_s⁽⁰⁾, i s.

Среди найденных невязок вновь отыскиваем наибольшую по мо- дулю R_k⁽¹⁾ и, положив x_k⁽²⁾ = x_k⁽¹⁾ + R_k⁽¹⁾, получаем очередные R_k⁽²⁾ = 0, R_i⁽²⁾ = R_i⁽¹⁾ + c_isR_k⁽¹⁾, i  k, и т. д. до получения максимума невязки в пределах заданной точности.

Пример. Обратимся к рассмотренной выше системе: 4 x₁ + 0.24 x₂ − 0.08 x₃ = 8,

0.09 x₁ + 3 x₂ − 0.15 x₃ = 9,

0.04 x₁ − 0.08 x₂ + 4 x₃ = 20.

Разделив на элементы главной диагонали, имеем

x₁ + 0.06 x₂ − 0.02 x₃ = 2,

0.03 x₁ + 3 x₂ − 0.05 x₃ = 3,

0.01 x₁ − 0.02 x₂ + x₃ = 5.

Преобразуем к виду, приемлемому для последующих итераций:

R₁ = 2 − x₁ − 0.06 x₂ + 0.02 x₃, R₂ = 3 − 0.03 x₁ − x₂ + 0.05 x₃, R₃ = 5 − 0.01 x₁ + 0.02 x₂ − x₃.

Задав x₁⁽¹⁾ = 2, x₂⁽¹⁾ = 3, x₃ = 5, получаем

R₁⁽²⁾ = −0.08, R₂⁽²⁾ = 0.19, R₃⁽²⁾ = 0.04.

Выбираем наибольшую невязку R₂⁽²⁾ = 0.19 и, согласно ^{(2.30), корректируем: x}2^{(2) = 3 + 0.19 = 3.19.}

Очевидно R₂⁽²⁾= 0,

R₁⁽²⁾ =R₁⁽¹⁾ – 0.06 R₂⁽¹⁾ = −0.08 – 0.06  0.19 = −0.0912,

R₃⁽²⁾ =R₃⁽¹⁾ + 0.02 R₂⁽¹⁾ = 0.04 + 0.02  0.19 = 0.0438.

Наибольшая невязка R₁⁽²⁾ = −0.0912 и x₁⁽³⁾ = 2 − 0.0912 = 1.9088. Отсюда R₁⁽³⁾ = 0,

R₂⁽³⁾ = R₂⁽²⁾ – 0.03 R₁⁽²⁾ = 0 – 0.03 (–0.0912) = 0.002736,

R₃⁽³⁾ = R₃⁽²⁾ – 0.01 R₁⁽²⁾ = 0.0438 – 0.01 (–0.0912) = 0.044712.

3 ³
Наибольшая невязка R⁽³⁾ = 0.044712, x⁽³⁾ = 5 + 0.044712 =

= 5.044712 и т. д.

Нетрудно увидеть, что объем вычислительной работы не больше, чем при использовании других итерационных методов.


Можно свести решение системы линейных уравнений

n

^{ a}ij^xj

j1

 b_i,

i 1, n

(2.32)

к задаче минимизации (до нуля) функции

n _ n

_2

_ g_i^ _ a_ijx_j b_i^

, g_i

• 
  0, i 1, n.
  

(2.33)

i1 _ j1 _

В самом деле, если решение (2.32) существует и оно един- ственно, то (2.33) обращается в нуль. В случае противоречивой системы достижение нуля нереально, и существенную роль игра- ет выбор весовых коэффициентов g_i, выражающих степень зна- чимости соблюдения того или иного уравнения (2.32). Очевидно, что решение задачи оптимизации не проще использования других рассмотренных здесь методов, требует знакомства с соответ- ствующими методами оптимизации и, может быть, даже с мето- дами случайных испытаний (методами Монте-Карло).

Мы не пытаемся рассмотреть все многообразие прямых и итерационных методов решения линейных алгебраических си- стем, большинство из которых потеряло свою практическую зна- чимость в век могущества вычислительной техники. Заметим только, что для систем высокого порядка, где матрица коэффици- ентов может быть разбита на блоки, среди которых есть нулевые, используют клеточные методы, сводящие исходную задачу к по- следовательному перебору клеток (блоков) матрицы и поиску со- ответствующих обратных матриц.

Особого внимания заслуживают и «плохообусловленные» системы, для которых определитель матрицы близок к нулю. Здесь малейшее изменение исходных данных ведет к значитель- ному изменению решения (решение неустойчиво по исходным

2.1 Метод дихотомии

Самым простейшим из методов уточнения корней является метод Больцано^** половинногоделенияили методдихотомии(бисекции).

Пусть непрерывная функция f (x) на концах отрезка [a, b] имеет значения разных знаков, т. е. f (a)  f (b) < 0. Другими слова- ми, на отрезке имеется хотя бы один корень. Возьмем середину отрезка x = (a + b) / 2. Если f (a)  f (x) < 0, то корень явно принад- лежит интервалу от aдо (a + b) / 2 и в противном случае от (a + b) / 2 до b. Берем подходящий из этих интервалов, вычисляем значение функции в его середине и т. д., пока длина очередного интервала не окажется меньше заданной предельной абсолютной погрешности (или выполнятся другие вышеупомянутые крите- рии). Так как каждое очередное вычисление f (x) сужает интервал поиска вдвое, то при исходном отрезке [a, b] и предельной по- грешности  количество вычислений nопределяется условием (b − a) / 2ⁿ< , или n log₂((b − a) / ). Например, при исходном единичном интервале и точности порядка шести знаков после де- сятичной точки достаточно провести лишь 20 вычислений значе- ний функции.

Если при некотором x = Z значения полинома и его производных неотрицательны (n-я про- изводная положительна), то Z может быть принято за верхнюю границу положительных корней полинома.

Возьмем полином P(−x) = −x5 − 4 x4 − 5 x3 + 6 x + 4. Для рас- сматриваемого полинома и его производных, например при x = 2.5 P(x) = x5 − 4 x4 + 5 x3 − 6 x + 4 = 8.53125, P(x) = 5 x4 −

– 16 x3 + 15 x2 − 6 = 33.0625, P″(x) = 20 x3 – 48 x2 + 30 х = 87.5,

P(3)(x) = 60 x2 – 96 х + 30 = 165, P(4)(x) = 120 x – 96 = 204,

P(5)(x) = 120. Значения положительны и можно утверждать, что верхняя граница для положительных корней не превышает 2.5.

Если обратиться к уравнению –P(−x) = − (x5 + 4 x4 + 5 x3 −

– 6 x − 4) = 0 и получить для −P(–x) аналогичные оценки при х = 2.5, получаем право утверждать, что нижняя граница для от- рицательных корней не менее −2.5.

Иногда оказываются полезными и следующие утверждения.

2.2 Метод хорд

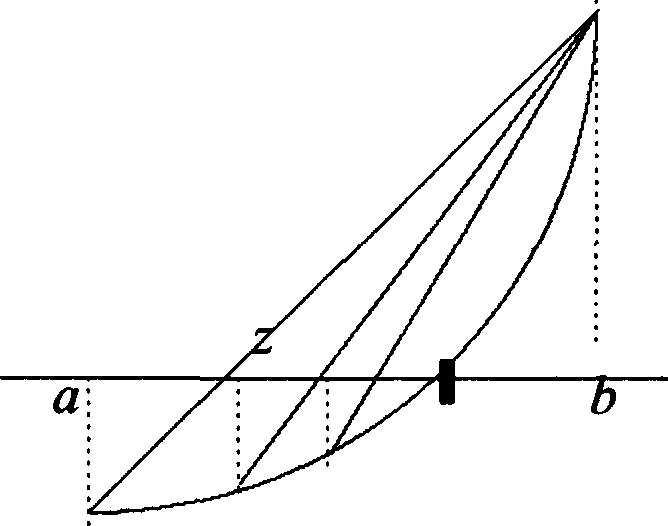В отличие от метода дихотомии, обращающего внимание лишь на зна- ки значений функции, но не на сами значения, методхордиспользует пропорциональное деление интервала . Здесь вычисляются значе- ния функции на концах интервала, и строится «хорда», соединяющая точки (a, f(a)) и (b, f(b)). Точка пере-

Рис.3.4

сечения ее с осью абсцисс

_z af(b)bf(a)

f(b)  f(a)

принимается за очередное приближение к корню. Анализируя знак f (z) в сопоставлении со знаком f (x) на концах интервала, сужаем интервал до [a, z] или [z, b] и продолжаем процесс по- строения хорд до тех пор, пока разница между очередными при- ближениями не окажется достаточно малой (в пределах допусти- мой погрешности).

Доказано, что истинная погрешность найденного приближе-

ния

X^*  Z_n

 ^MmZ_n Z_n1 ,

m
где X^* − корень уравнения, Z_nи Z_n–1 − очередные приближения; mи M − наименьшее и наибольшее значения |f (x)| на отрезке [a, b]. В случае так называемых быстро осциллирующих функций,

где в небольшой окрестности корня значения функции меняются весьма значимо, условие завершения итераций можно взять в ви- де |f(x)| < ε.

2.3 Метод Ньютона – Рафсона (метод касательных)

Другую обширную группу методов уточнения корня пред- ставляют итерационные методы, в отличие от методов дихотомии и хорд требующие задания не начального интервала местонахож- дения корня, а его начального приближения.

Наиболее популярным из таких методов является метод Ньютона − Рафсона (метод касательных). Пусть известно неко- торое приближенное значение Z_nкорня X^*. Применяя формулу Тейлора

f(Z_n

 h) 

f(Z_n

)  hf'(Z_n

)  ^h2

2!

f''(Z_n

)  ...  ^hn

n!

_f(n) _(Zn

)  ...

и ограничиваясь в ней двумя членами, имеем

f(Z_n+ h)  f(Z_n) + h f(Z_n) = 0,

откуда
h= −

f(Z_n) _{, Z}

f '(Z_n)


n+1
= Z_n−

^f(Zn) .

f'(Z_n)

Число положительных кор- ней полинома равно числу перемен знаков в системе его коэффи- циентов или меньше этого числа на четную величину.

Так для уравнения P(x) = x⁵ − 4 x⁴ + 5 x³ − 6 x + 4 = 0 (нуле- вые коэффициенты не учитываются) число положительных кор- ней равно 4 или 2. Если взять P(−x) = − (x⁵ + 4 x⁴ + 5 x³ − 6 x− 4) =

= 0, то число перемен знаков равно 1 и исходное уравнение имеет один отрицательный корень Если полином с вещественными коэффициентами имеет только действительные корни, то система его коэффициентов удовлетворяет условию

a²  a a ( k 1, 2,…, n1) .

k k1 k1

Обратите внимание, что обратное утверждение неверно. Например, полином P(x) = x² − 4 x + 5 , где 4² > 1 ∙ 5, обладает двумя комплексными корнями.


Геометрически этот метод предлагает построить касатель-

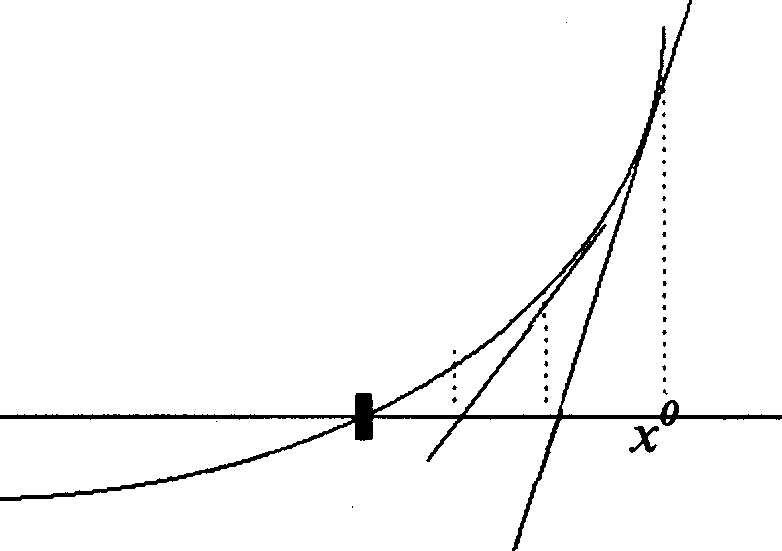ную к кривой y = f (x) в выбран- ной точке x = Z_n, найти точку пе- ресечения ее с осью x и принять эту точку за очередное прибли- жение к корню

Очевидно, метод касатель- ных обеспечивает сходящийся процесс приближений лишь при

Рис.3.5

выполнении некоторых условий: в зависимости от выбора началь-

ного приближения и особенностей f(x) может возникнуть расхо-

дящийся процесс или уход к другому корню
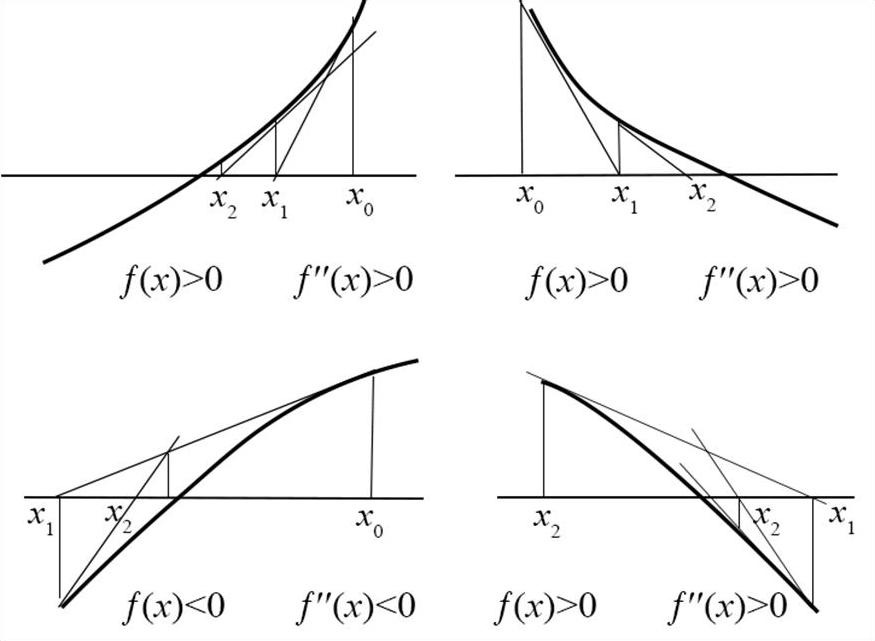
В случае функций, непрерывных на [a, b] вместе со своими производными, для выбора начального приближения полезна следующая теорема [1, 2, 4].

Теорема. Если f (a) f (b) < 0, f (a) и f (b) ≠ 0 и знакопостоян- ны на [a, b], то при соблюдении f (z₀) f (z₀) > 0, z₀  [a, b] итера- ционный процесс сходится

Очевидно, что для функций, производная от которых в окрестности корня близка к нулю, использовать метод Ньютона едва ли разумно.

Вернемся к формуле Тейлора учитывая на единицу большее число слагаемых

f(Z_n

 h) 

f(Z_n

)  hf'(Z_n

)  ^h2

2!

f''(Z_n) 

f(Z_n

)  h^ f'(Z

_ n

)  ^h

2

f''(Z_n

)^  0 .

_

Положив внутри скобок h= −

^f(Zn) , получаем

f '(Z_n)

f(Z_n

 h) 

f(Z_n

)  h^ f' (Z

_ n