ЛЕКЦИЯ-5 полиномы и графики двумерных функций. Значение полинома, найти корни полинома, выполнить операции умножения
 Скачать 296 Kb.
|
|
ЛЕКЦИЯ 5 Операции над полиномами В системе MATLAB имеется большое количество функций для работы с полиномами, с использованием которых можно вычислить значение полинома, найти корни полинома, выполнить операции умножения и деления полиномов, произвести дифференцирование и интегрирование полиномов. Как известно, полином (или многочлен) – это выражение вида  ,где  – постоянные коэффициенты.В MATLAB полином задается и хранится в виде вектора, элементами которого являются коэффициенты полинома  .Так, например, для задания полинома  следует ввести команду:>> p=[5 -4 2 -1 8] p = 5 -4 2 -1 8 1. Вычисление значения полинома. Для вычисления значения полинома от некоторого аргумента предназначена функция polyval, имеющая следующий синтаксис: y=polyval(p,x) где p – вектор коэффициентов полинома; x – значение аргумента. В частности, для рассматриваемого полинома можем вычислить >> polyval(p,2) ans = 62 В качестве аргумента может быть задан вектор или матрица. В этом случае значение полинома будет вычислено для каждого элемента данного вектора или матрицы, в результате чего будет сформирован вектор или матрица того же размера, что и аргумент x. Например: >> p=[2 0 4 6]; >> x=[1 3; 2 7]; >> y=polyval(p,x) y = 12 72 30 720 Пример выполнения лабораторной работы. Пример 1. Табулирование полинома  на отрезке [ ,  ] с последующим построением графика, а также выдачей максимального и минимального значения функции и точек, где эти значения достигаются, ,  ,  Пример текста М-файла p=input('ввести коэффициенты полинома: [a(n),a(n-1),...,a(1),a(0)]='); xn=input('ввести начальное значение xn='); xk=input('ввести конечное значение xk='); n=input('ввести значение n='); h=(xk-xn)/n; x=xn:h:xk; y=polyval(p,x); [fmin,imin]=min(y); [fmax,imax]=max(y); fprintf('\n fmin=%8.2f в точке xmin=%6.2f \n fmax=%8.2f в точке xmax=%6.2f \n',fmin,x(imin),fmax,x(imax)) plot(x,y),grid on Результаты счета ввести коэффициенты полинома: [a(n),a(n-1),...,a(1),a(0)]=[1 4 -6 12 -1] ввести начальное значение xn=-5 ввести конечное значение xk=5 ввести значение n=20 fmin= -145.00 в точке xmin= -4.00 fmax= 1034.00 в точке xmax= 5.00 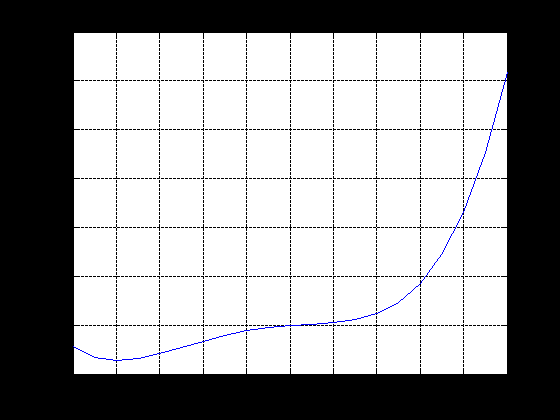 2. Вычисление корней полинома. Вычислить все корни полинома можно с помощью функции roots (причем число корней полинома всегда совпадает со степенью полинома). Вычислив корни полинома, можно восстановить коэффициенты приведенного полинома (т.е. полинома, у которого коэффициент при старшей степени равен 1). Для этих целей в MATLAB имеет функция poly: >> p=[2 -6 6 -6 4]; >> r=roots(p) r = 2.0000 + 0.0000i 0.0000 + 1.0000i 0.0000 - 1.0000i 1.0000 + 0.0000i >> p1=poly(r) p1 = 1.0000 -3.0000 3.0000 -3.0000 2.0000 Для того, чтобы получить коэффициенты исходного полинома, следует умножить полученные вектор коэффициентов на коэффициент при старшей степени полинома (в рассматриваемом примере он равен 2): >> p1*2 ans = 2.0000 -6.0000 6.0000 -6.0000 4.0000 Пример 2. Найти корни полинома ,Пример текста М-файла p=input('ввести коэффициенты полинома: [a(n),a(n-1),...,a(1),a(0)]='); r=roots(p); fprintf('\n корни полинома:\n'),disp(r) Результаты счета вести коэффициенты полинома: [a(n),a(n-1),...,a(1),a(0)]=[1 4 -6 12 -1] корни полинома: -5.4953 0.7042 + 1.2643i 0.7042 - 1.2643i 0.0869 >> 3. Умножение и деление полиномов. Для выполнения операций умножения и деления полиномов в системе MATLAB имеются функции conv и deconv. Функция conv вычисляет так называемую свертку векторов (построение расширенного вектора коэффициентов по заданным векторам коэффициентов полиномов-сомножителей), а функция deconv производит обратную свертку векторов (вычисление векторов коэффициентов полиномов, являющихся частным и остатком от деления одного полинома на другой. Функция conv имеет следующий синтаксис: w=conv(u,v) где w – вектор коэффициентов полинома, полученного в результат перемножения полиномов, заданных векторами u и v. Например, имеем: >> u=[1 2 3 4 5]; >> v=[1 3 5]; >> w=conv(u,v) w = 1 5 14 23 32 35 25 Пример 3. Табулирование полиномов ,  и их произведения  на отрезке [, ] с последующим построением графиков, ,  ,  , Пример текста М-файла p=input('ввести коэффициенты полинома P: [p(n),p(n-1),...,p(1),p(0)]='); q=input('ввести коэффициенты полинома Q: [q(n),q(n-1),...,q(1),q(0)]='); r=conv(p,q); xn=input('ввести начальное значение xn='); xk=input('ввести конечное значение xk='); n=input('ввести значение n='); h=(xk-xn)/n; x=xn:h:xk; yp=polyval(p,x); yq=polyval(q,x); yr=polyval(r,x); hold on plot(x,yp,'r',x,yq,'b',x,yr,'g'),grid on legend('P','Q','R=PQ',0) Результаты счета ввести коэффициенты полинома P: [p(n),p(n-1),...,p(1),p(0)]=[2 -9] ввести коэффициенты полинома Q: [q(n),q(n-1),...,q(1),q(0)]=[1 -4 3] ввести начальное значение xn=0 ввести конечное значение xk=5 ввести значение n=20 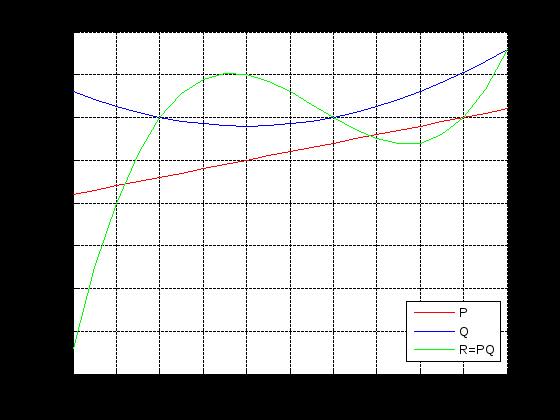 Синтаксис функции deconv следующий: [q,r]=deconv(u,v) где q и r – векторы коэффициентов полинома-результата (частного) и полинома-остатка, полученных в результате деления полиномов, заданных векторами u и v. Рассмотрим пример: >> u=[1 2 3 4 5]; >> v=[1 3 5]; >> [q,r]=deconv(u,v) q = 1 -1 1 r = 0 0 0 6 0 Для того, чтобы определить только лишь частное, следует обратиться к функции deconv следующим образом: >> q=deconv(u,v) q = 1 -1 1 Пример 4. Табулирование полиномов , и их частного  на отрезке [, ] с последующим построением графиков, ,  ,  , .Пример текста М-файла p=input('ввести коэффициенты полинома P: [p(n),p(n-1),...,p(1),p(0)]='); q=input('ввести коэффициенты полинома Q: [q(n),q(n-1),...,q(1),q(0)]='); r=deconv(p,q); xn=input('ввести начальное значение xn='); xk=input('ввести конечное значение xk='); n=input('ввести значение n='); h=(xk-xn)/n; x=xn:h:xk; yp=polyval(p,x); yq=polyval(q,x); yr=polyval(r,x); hold on plot(x,yp,'r',x,yq,'b',x,yr,'g'),grid on legend('P','Q','R=P/Q',0) Результаты счета ввести коэффициенты полинома P: [p(n),p(n-1),...,p(1),p(0)]=[1 -6 11 -6] ввести коэффициенты полинома Q: [q(n),q(n-1),...,q(1),q(0)]=[1 -5 6] ввести начальное значение xn=0 ввести конечное значение xk=4 ввести значение n=20 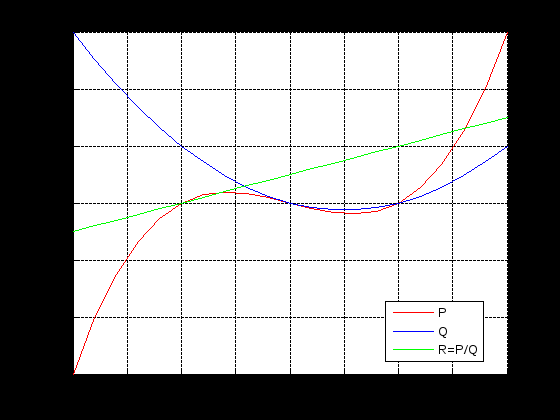 4. Дифференцирование и интегрирование полиномов. Для нахождения производной от полинома можно использовать функцию polyder, к которой можно обратиться различными способами (в зависимости от необходимого результата): q=polyder(p) – выполняется вычисление вектора коэффициентов полинома-производной (q) от исходного полинома, заданного вектором коэффициентов p; c=polyder(a,b) – выполняется вычисление производной от произведения двух полиномов, заданных векторами коэффициентов a и b; [q,d]=polyder(a,b) – выполняется вычисление производной от отношения двух полиномов, заданных векторами коэффициентов a и b, причем результат выдается в виде отношения полиномов q и d, т.е. q/d. Пусть, например, требуется вычислить производную от уже рассматривавшегося выше полинома . Имеем:>> p=[5 -4 2 -1 8]; >> q=polyder(p) q = 20 -12 4 -1 Вычислим теперь производную от произведения двух полиномов: >> a=[1 2 9]; >> b=[-4 7]; >> c=polyder(a,b) c = -12 -2 -22 Заметим, что тот же результат можно получить, если предварительно перемножить полиномы с использованием функции conv, после чего определить производную от этого произведения: >> p=conv(a,b) p = -4 -1 -22 63 >> c=polyder(p) c = -12 -2 -22 Для интегрирования полиномов служит функция polyint, имеющая следующий синтаксис: q=polyint(p,k) где k – константа (постоянная) интегрирования, которая может быть опущена (по умолчанию принимается равной нулю). Приведем пример: >> p=[2 5 7 -4]; >> q=polyint(p) q = 0.5000 1.6667 3.5000 -4.0000 0 Пример 5. Табулирование полинома , его производных и первообразной на отрезке [, ] с последующим построением графиков,, , Пример текста М-файла p4=input('ввести коэффициенты полинома: [a(n),a(n-1),...,a(1),a(0)]='); p3=polyder(p4); % 1-я производная p2=polyder(p3); % 2-я производная p1=polyder(p2); % 3-я производная p0=polyder(p1); % 4-я производная p5=polyint(p4); % 1-я первообразная xn=input('ввести начальное значение xn='); xk=input('ввести конечное значение xk='); n=input('ввести значение n='); h=(xk-xn)/n; x=xn:h:xk; y0=polyval(p0,x); y1=polyval(p1,x); y2=polyval(p2,x); y3=polyval(p3,x); y4=polyval(p4,x); y5=polyval(p5,x); hold on plot(x,y4,'r',x,y3,'b',x,y2,':b',x,y1,'c',x,y0,'m',x,y5,'g'),grid on legend('P','dP','d2(P)','d3(P)','d4(P)','int(P)',0) Результаты счета ввести коэффициенты полинома: [a(n),a(n-1),...,a(1),a(0)]=[1 4 -6 12 -1] ввести начальное значение xn=-5 ввести конечное значение xk=5 ввести значение n=20 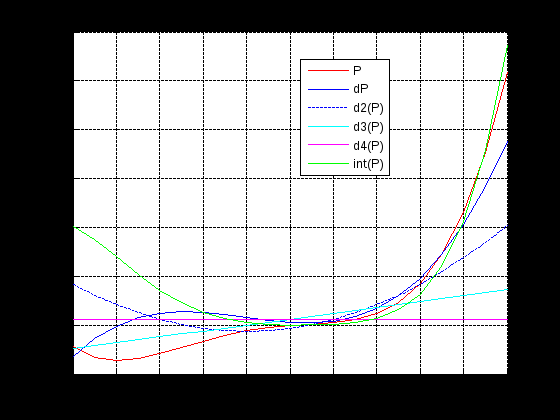 Пример 6. Табулирование полинома ,  , производной от  : на отрезке [ , ] с последующим построением графиков, где ,  ,т.е.  и  , , Пример текста М-файла p=input('ввести коэффициенты полинома P : [a(n),a(n-1),...,a(1),a(0)]='); q=input('ввести коэффициенты полинома Q: [a(n),a(n-1),...,a(1),a(0)]='); [t r]=polyder(p,q) % производная P/Q [tr rr]=deconv(t,r) % tr-коэффициенты полинома TR частного и остатка RR от деления T/R xn=input('ввести начальное значение xn='); xk=input('ввести конечное значение xk='); n=input('ввести значение n='); h=(xk-xn)/n; x=xn:h:xk; P=polyval(p,x); Q=polyval(q,x); T=polyval(t,x); R=polyval(r,x); TR=polyval(tr,x); RR=polyval(rr,x); plot(x,P,x,Q,x,T,x,R,x,TR,x,RR),grid on legend('P','Q','T=dP*Q-P*dQ','R=Q^2','TR=[T/R]','RR=mod(T/R)',0) Результаты счета ввести коэффициенты полинома P : [a(n),a(n-1),...,a(1),a(0)]=[1 0 1] ввести коэффициенты полинома Q: [a(n),a(n-1),...,a(1),a(0)]=[1 0] t = 1 0 -1 r = 1 0 0 tr = 1 rr = 0 0 -1 ввести начальное значение xn=1 ввести конечное значение xk=2 ввести значение n=20 >> 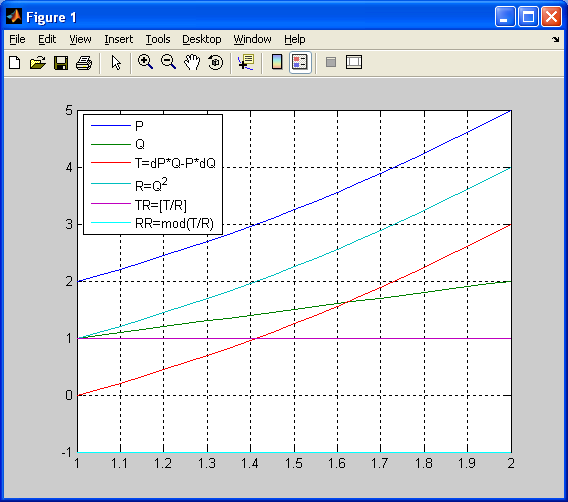 Графическое построение двумерных функций, заданных на прямоугольной области. Рассмотрим некоторые возможности МАТЛАБ на примере функции  ,  Примеры отдельных текстов М-файлов Построение сеточной области xy=input('[xa ya;xb yb]='); dl=xy(2,:)-xy(1,:); n=input('[n1 n2]='); h=dl./n; x1=xy(1,1):h(1):xy(2,1); x2=xy(1,2):h(2):xy(2,2); [x y] = meshgrid(x1,x2); U=-log(x.^2+y.^2+1); Ввод исходных данных в командном окне [xa ya;xb yb]=[-3 -4;3 4] [n1 n2]=[10 20] Использование функции surf figure() surf(x,y,U) title('SERF: function U') colormap hsv colorbar; axis image; xlabel('X'),ylabel('Y'),zlabel('z=U(x,y)') 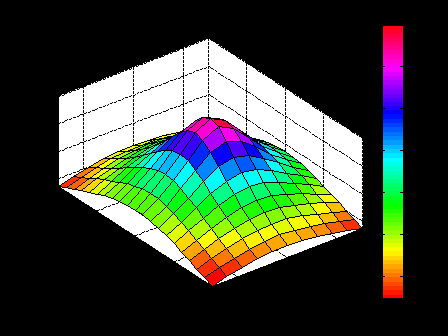 figure() surf(x,y,U) title('SERF: function U') colormap hsv colorbar; %axis image; xlabel('X'),ylabel('Y'),zlabel('z=U(x,y)') 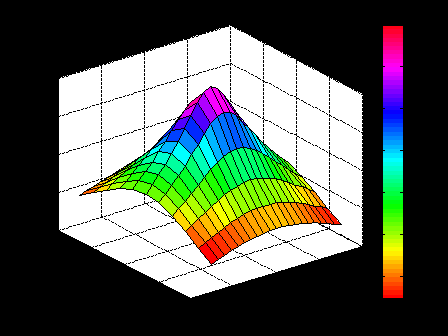 figure() surf(x,y,U) title('SERF: function U') colormap copper colorbar; axis image; xlabel('X'),ylabel('Y'),zlabel('z=U(x,y)') shading interp 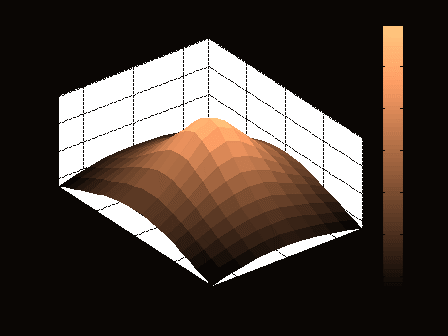 figure() surf(x,y,U) title('SERF: function U') colormap copper colorbar; axis image; xlabel('X'),ylabel('Y'),zlabel('z=U(x,y)') %shading interp 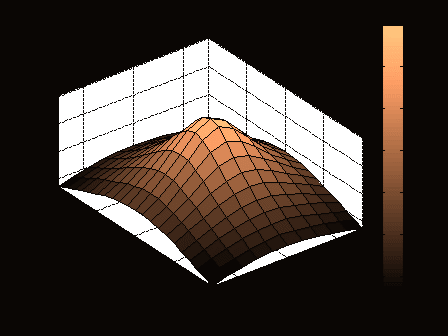 Использование функции plot3 figure() plot3(x,y,U,'LineWidth',8) grid on title('PLOT3: function U') colormap hsv axis image; xlabel('X'),ylabel('Y'),zlabel('z=U(x,y)') 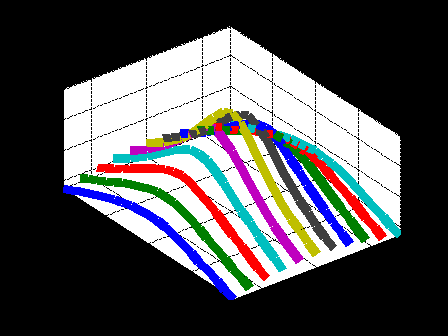 figure() %plot3(x,y,U,'LineWidth',8) plot3(x,y,U) grid on title('PLOT3: function U') colormap hsv axis image; xlabel('X'),ylabel('Y'),zlabel('z=U(x,y)') 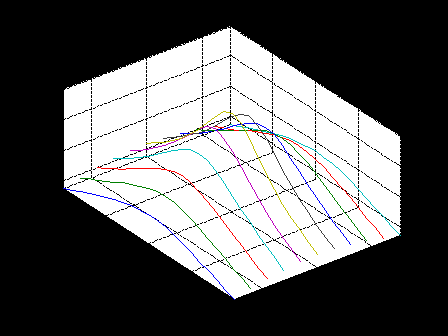 Использование функции contour3 figure() [C h]=contour3(x,y,U,10); set(h,'LineWidth',5) grid on title('COUNTOUR3: function U') colormap hsv colorbar; axis image; xlabel('X'),ylabel('Y'),zlabel('z=U(x,y)') 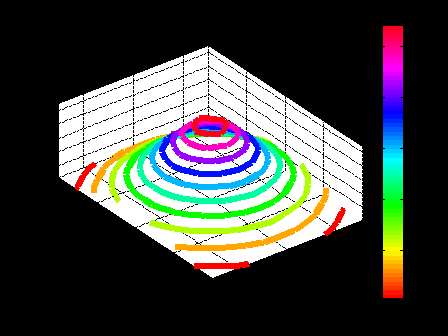 figure() %[C h]=contour3(x,y,U,10); set(h,'LineWidth',5) contour3(x,y,U,10); grid on title('COUNTOUR3: function U') colormap hsv colorbar; axis image; xlabel('X'),ylabel('Y'),zlabel('z=U(x,y)') 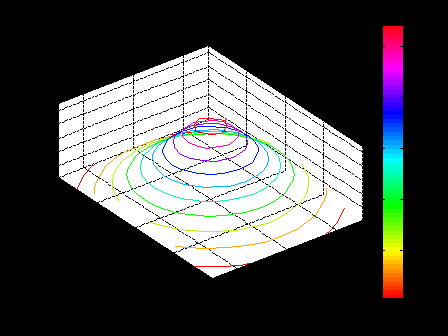 Использование функции contourf figure() contourf(x,y,U,8) title('CONTOURF: function U') colormap hsv colorbar; axis image; xlabel('X'),ylabel('Y') 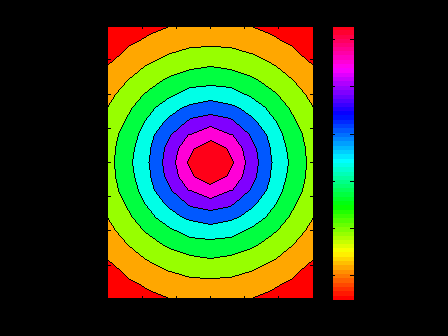 figure() contourf(x,y,U,8) title('CONTOURF: function U') %colormap hsv colorbar; axis image; xlabel('X'),ylabel('Y') 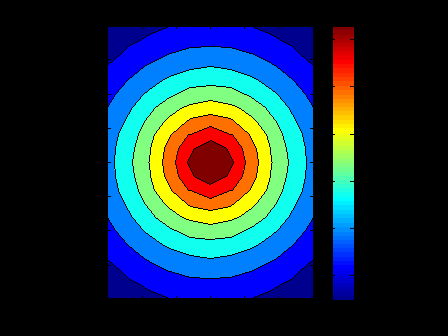 Использование функции contour figure() [C h]=contour(x,y,U,8); set(h,'LineWidth',2),clabel(C,h); title('CONTOUR: function U') colormap gray colorbar axis image; xlabel('X'),ylabel('Y') 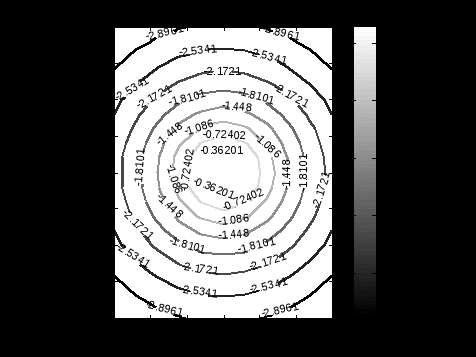 figure() %[C h]=contour(x,y,U,8); set(h,'LineWidth',2),clabel(C,h); contour(x,y,U,8); title('CONTOUR: function U') %colormap gray colorbar %axis image; xlabel('X'),ylabel('Y') 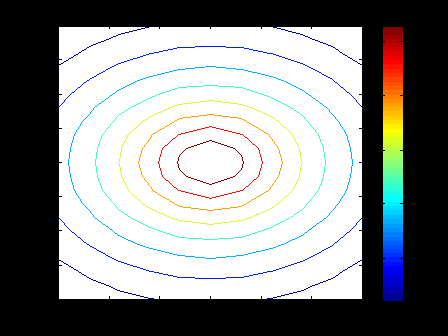 |