Курсавая. Курсавая 1. Методы решения алгебраических и трансцендентных уравнений
 Скачать 0.64 Mb.
|
|
Предположим, что процесс отделения корней проведен и на отрезке [a, b] находится ровно один корень ξ уравнения f(x)=0. Необходимо определить его положение с погрешностью . Метод половинного деления заключается в следующем, Сначала определяем середину с отрезка [a, b] c = (a+b)/2 и вычисляем значение функции f(c). Далее делаем выбор, какую из двух частей взять для уточнения корня. Очевидно, что корень будет находиться в той половине переприсваивая новому значению bзначение c . Если же реализуется ситуация, когда функция имеет разные знаки на концах отрезка [c, b], то из рассмотрения следует исключить отрезок [a, c], формально переприсваивая новому значению азначение c. В результате мы получим последовательность вложенных друг в друга отрезков все уменьшающейся длины: [a1, b1], [a2 , b2 ],...[an, bn]. Этот повторяющийся (итерационный) процесс будем продолжать до тех пор, пока длина отрезка [an, bn] не станет меньше заданной погрешности вычислений. Тогда искомый корень an bn (an+bn)/2. (2) 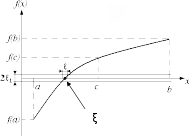 Графическая интерпретация метода половинного деления Следует учитывать, что функция f(x) вычисляется с некоторой абсолютной погрешностью . Вблизи корня значения функции f(x) малы по абсолютной вели- чине и могут оказаться сравнимыми с погрешностью ее вычисления. Другими словами, при подходе к корню мы можем попасть в “полосу шумов” 21 и дальнейшее уточнение корня становится бессмысленным. Поэтому надо за- дать ширину “полосы шумов” и прекратить итерационный процесс при попадании в нее. Также необходимо иметь в виду, что при уменьшении длины интервала [an, bn] увеличивается погрешность вычисления его длины an bnза счет вычи- тания двух близких чисел. Метод половинного деления обладает довольно большой скоростью сходи- мости. Так как за каждую итерацию интервал, где расположен корень, уменьшает- ся в два раза, то через nитераций длина интервала будет равна (b−a)/2n. За 10 итераций интервал уменьшится в 220 раз. 210 1024 103 раз, а за 20 итераций – в Приведем вычислительную схему подпрограммы, реализующей метод деле- ния отрезка пополам. 1.3 Метод Гаусса Пусть a11 0. Первое уравнение делим на a11 и исключаем x1 из последующих уравнений. Если коэффициент при x2 во втором уравнении отличен от нуля, то второе уравнение делим на этот коэффициент и исключаем x2 из последующих уравнений. Про- должая аналогичную процедуру, в результате получим систему с так называемой верхней треугольной матрицей коэффициентов при неизвестных x1 + с12 x2 + с13 x3 + … + с1 n–1 xn–1 + с1 nxn= d1, x2 + с23 x3 + … + с2 n–1 xn–1 + с2 nxn= d2, . . . .. . . .. . .. . . .. . .. . . .. . . .. . .. . . .. .. .. . . .. . . xn-1 + cn–1 nxn= dn–1, xn= dn. Выполнив такую процедуру «прямого хода», затем выпол- няем «обратный ход» поиска значений переменных n xn dn, xk dk ckjxj, k jk1 n 1, n 2,…, 2,1. В этом случае общее количество арифметических операций при n> 7 имеет порядок N 2n(n 1)(n2) n(n1) n3, т. е. такой 3 подход является менее трудоемким, чем правило Крамера. Реше- ние ранее рассмотренного примера в этой схеме имеет вид:
В результате получаем решение системы x3 = 3, x2 = 10 − (3) 3 = 1, x1 = 5/3 − (0) 3 − (–1/3) 1 = 2. Заметим, что произведение всех возникающих здесь делителей («ведущих элементов») дает определитель матрицы коэф- фициентов. Очевидно, что при обращении в нуль ведущих эле- ментов приходится переставлять строки (уравнения) или столбцы (переменные). Другая эквивалентная по затратам схема полного исклю-чения отличается лишь тем, что исключение переменных выпол- няется не только из последующих, но и из предыдущих уравне- ний. Эта схема применима и для поиска обратной матрицы (если к матрице A Bприсоединить единичную, то после действий полного исключения на месте матрицы A B E получится мат- рица E X A–1). Например:
  В случае ведущих элементов, близких к нулю, погрешность вычислений значимо возрастает и часто, особенно в случае больших n, можно получить решение, далекое от истины. Во избежание такого эффекта практически во всех программных реализациях метода Гаусса используют схему главных элементов. Здесь сначала в качестве ведущего выбирается наибольший по модулю элемент матрицы коэффициентов, соответствующее уравнение делится на этот элемент и соответствующая переменная исключается из остальных уравнений. На следующих шагах решения за ведущий принимается наибольший по модулю элемент преобразованной матрицы без учета ранее рассмотренных уравнений (если ведущий элемент окажется нулевым, то либо система не имеет решений, либо система имеет бесчисленное множество решений). Например:
|