Шпаргалка по методам оптимизации. Шпоры. Алгоритм пассивного поиска минимума

• Название: Алгоритм пассивного поиска минимума
• Анкор: Шпаргалка по методам оптимизации
• Дата: 09.06.2022
• Размер: 468.5 Kb.
• Имя файла: Шпоры.doc
• Тип: Документы; #581813
• страница: 1 из 3

Алгоритм пассивного поиска минимума

Отрезок [a,b] исходный отрезок неопределенности. Пусть N- число точек, в которых необходимо провести вычисления целевой функции f(x), т.е. N экспериментов. Точки, в которых необходимо провести эксперименты, определяются следующим образом:



Среди вычисленных значений {f(x_i)} (i=1,N), ищется точка x_j , в которой достигается минимум:

f(x_j)= min f(x_i) 1iN

Найденная точка принимается за приближенное решение задачи . Исходный отрезок неопределенности [a,b] после экспериментов в N точках сужается до [x_j-1,x_j+1], длина которого равна:



Точность найденного решения равна половине отрезка неопределенности, т.е. , где и x^* - точное решение.

Алгоритм равномерного блочного поиска

Схема алгоритма

Шаг 1. Задаются исходный отрезок неопределенности [a,b],  - точность приближенного решения , число экспериментов в блоке – n (нечетное, n=2k-1). Проводим эксперимент в середине отрезка [a,b], т.е. вычисляем y_k=f(x_k), где xk=(a+b)/2.

Шаг 2. Проводим эксперименты в остальных точках блока: y_i=f(x_i), где x_i=a+i*(b-a)/(n+1), i=1,2,..,n, ik. Находим точку x_j, в которой достигается минимум среди вычисленных значений: f(x_j)=min f(x_i), следовательно, точное значение минимума x^* содержится на отрезке [x_j-1,x_j+1].

Шаг 3. Полагаем a=x_j-1, b=x_j+1, x_k=x_j, y_k=y_j. Если b-a2, то , и поиск заканчивается. Иначе перейти к шагу 2. Если заданная точность  достигнута после т итераций, т.е. после экспериментов в m блоках, то длина отрезка неопределенности после всех N вычислений (N=n+(m-1)(n-1)=(n-1)m+1) будет:

и

Алгоритм деления интервала пополам

Это вариант предыдущего алгоритма при n=3.

Схема алгоритма.

Шаг 1. Задаются a,b,. Производим эксперимент в точке x₂=(a+b)/2, т.е. вычисляем y₂=f(x₂).

Шаг 2. Проводим эксперименты в остальных точках блока: x₁=(a+x₂)/2, y₁=f(x₁), x₃=(x₂+b)/2, y₃=f(x₃).

Находим x_j такую, что f(x_j)=min {f(x_i)}.

1 ≤ i ≤ 3 Тогда точное решение x* содержится на отрезке [x_j-1,x_j+1]. Предполагается .

Шаг 3. Полагаем a=x_j-1, b=xj+1, x₂=x_j, y₂=y_j. Если b-a2, то и поиск заканчивается. Иначе перейти к шагу 2.

После к итераций общее число проведенных экспериментов равно N=2к+1, а длина получившегося отрезка неопределенности будет , где [z] – целая часть числа z. Следовательно, достигнутая точность будет , =1/2L_N.

Метод дихотомии

Это алгоритм блочного поиска для ni=n=2, т.е. когда в блоке два эксперимента. Так как пассивная составляющая алгоритма, т.е. блок, содержит четное число экспериментов, то оптимальный выбор точек x_ij, в которых необходимо провести эксперименты, будет неравномерным, в отличие от предыдущих алгоритмов, где число экспериментов в блоке было нечетным и, соответственно, расположение точек равномерным. Если блок содержит два эксперимента, то оптимальное (дельта оптимальное) расположение точек, в которых будут проводится эксперименты, это как можно ближе к середине отрезка. Такое расположение точек позволяет получить наименьший отрезок неопределенностей после экспериментов в блоке.

Схема алгоритма.

Шаг 1. Задаются a,b, и  - малое положительное число, значительно меньшее чем .

Шаг 2. Определяется середина отрезка x=(a+b)/2. Производятся эксперименты в двух точках близких середине: y1=f(x-), y2=f(x+).

Шаг 3. Определяется следующий отрезок локализации, т.е. определяется какой из отрезков [a,x+] или [x-,b] содержит точное решение x*. Если y₁y₂, то это отрезок [a,x+] и b=x+, иначе это отрезок [x-,b] и a=x-, т.е. выбранный отрезок локализации мы снова обозначили как [a,b].

Шаг 4. Если b-a2, то x=(a+b)/2, и поиск заканчивается. Иначе перейти к шагу 2.

После к итераций общее число экспериментов будет N=2к, а длина получившегося отрезка неопределенности . Следовательно, .ъ

Метод золотого сечения

Для того чтобы уменьшить отрезок неопределённости [a,b], нам необходимо вычислить значение целевой функции f(x), по крайней мере, в двух точках на отрезке [a,b].

В результате этих двух экспериментов отрезок неопределённости сузится до отрезка [a,x₂] или [x₁,b]. Так как у нас нет никаких оснований предпочесть один из этих вариантов, то точки x₁ и x₂ должны быть симметричны относительно середины отрезка [a,b]. В этом случае длины отрезков [a,x₂] и [x₁,b] будут равны. Таким образом, остаётся вопрос как выбрать точку x₁.

В методе золотого сечения точка x₁ выбирается из соображения, что должно выполняться соотношение:



т.е. точка x₁ делит отрезок [a,b] по правилу «золотого сечения», где λ - есть «золотое отношение». Точка x₂ определяется как точка симметричная к x₁ относительно середины отрезка.

В результате экспериментов у нас получается отрезок неопределённости [a,x₂], содержащий точку x₁, или отрезок неопределённости [x₁б], содержащий точку x₂. Оказывается, что остающаяся точка на суженном отрезке неопределённости делит его вновь по правилу «золотого сечения». Следовательно, чтобы, в свою очередь, уменьшить новый отрезок неопределённости, нам не достаёт одного эксперимента, а именно, вычисления целевой функции в точке, симметричной к оставшейся точке относительно середины этого нового отрезка. Всё продемонстрировано на рисунке,

а)

б)

где буквы со штрихами обозначают новый отрезок неопределённости. Вариант а) соответствует случаю, если новым отрезком неопределённости будет [a,x₂], а вариант б) – отрезку [x₁,b].

В приводимой ниже схеме алгоритма остающиеся отрезки неопределённости переименовываются каждый раз как [a,b], а точки, в которых проводятся эксперименты на этом отрезке, обозначается через x₁ и x₂, причём . Кроме того, y₁ и y₂ имеют следующие значения: y₁ =f(x₁) и y₂ =f(x₂).
Схема алгоритма

Шаг1. Задаются a,b,ε и λ=1.618… Вычисляют .

Шаг2. а) Если 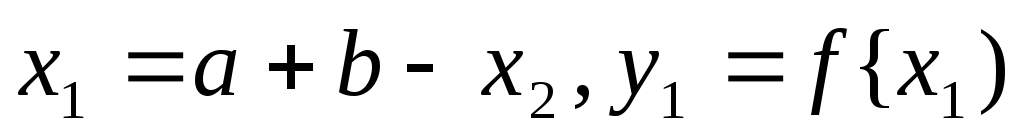, то полагают и вычисляют .

б) Если y₁>y₂, то полагают и вычисляют .

Шаг3. Если b-a>ε, то переходят к шагу 2. Иначе если y₁2, то полагают и если y₁≥y₂, то полагают и

Закончить поиск.

После каждой итерации длина отрезка неопределённости уменьшается в λ раз. Так как первая итерация начинается после двух экспериментов, то после N экспериментов длина отрезка неопределённости будет .

Метод чисел Фибоначчи

Этот метод применяется, когда число экспериментов N заранее задано. Метод чисел Фибоначчи, также как и метод золотого сечения относится к симметричным методам, т.е. точки, в которых выполняются два эксперимента, на основе которых происходит уменьшение отрезка неопределённости, расположены симметрично относительно середины отрезка. Вот только выбор точки x₁ происходит на основе других соотношений. Для этого используются числа Фибоначчи: , где и F₀=F₁=1.Точка x₁ определяется из соотношения:



т.е. . Точка x₁ делит [a,b] на две неравные части. Отношение малого отрезка к большему равно . Точка x₂ определяется как точка, симметричная к x₁ относительно середины отрезка [a,b]. Поэтому . При этом будет выполняться условие x₁2.

В результате экспериментов в точках x₁ и x₂ у нас получится отрезок неопределённости [a,x₂], содержащий точку x₁, или отрезок неопределённости [x₁,b], содержащий точку x₂. Остающаяся точка делит новый отрезок неопределённости на две неравные части в отношении:

. То 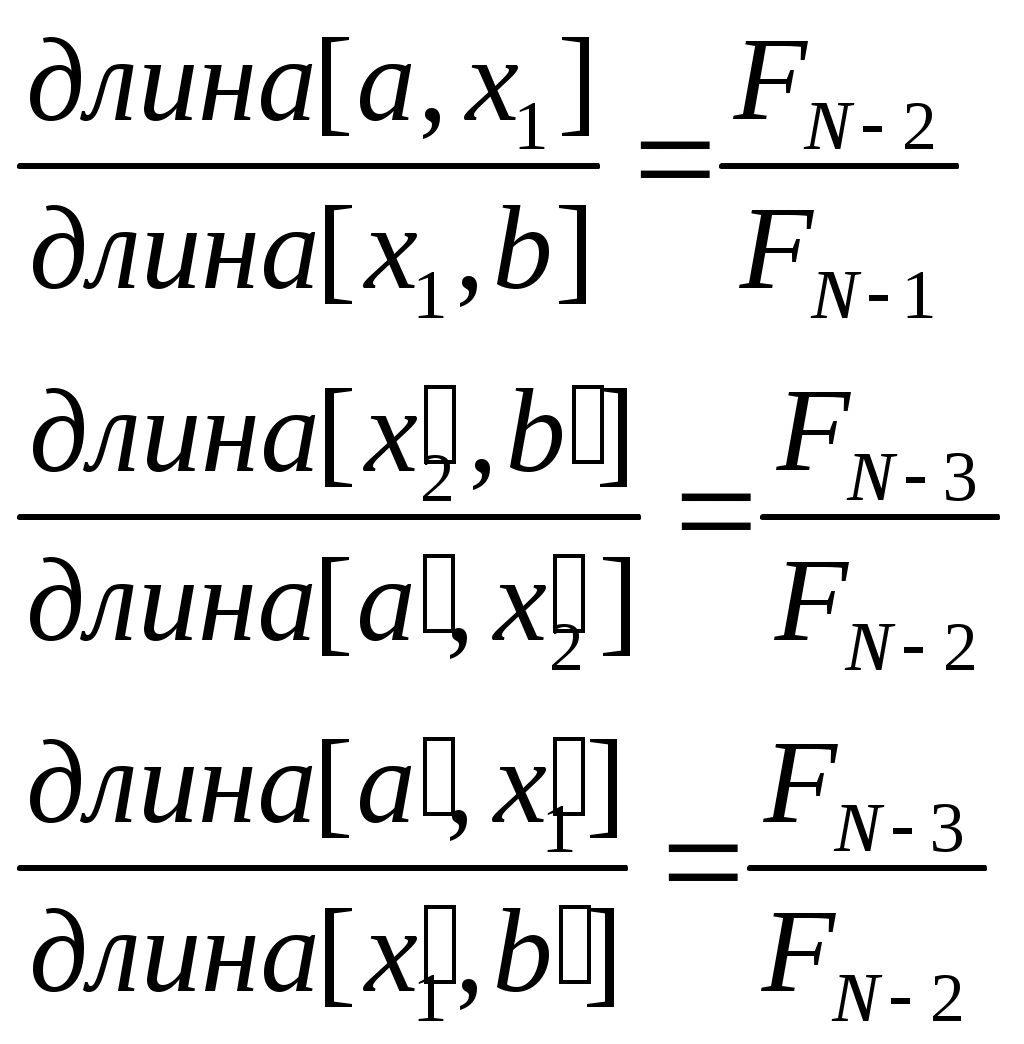есть в методе Фибоначчи остающаяся точка делит отрезок на две неравные части в пропорциях определяемых числами Фибоначчи. Так на к-ом шаге это отношение равно а длины отрезков равны: и . Всё это показано на рисунке:

а)

б)



Для того чтобы в свою очередь уменьшить получившийся отрезок неопределённости, надо определить симметричную точку относительно середины отрезка и произвести эксперимент в ней. Этот процесс продолжается, пока не будет проведено N экспериментов.

Схема алгоритма

Шаг 1. Задаются a,b,N Вычисляются числа Фибоначчи 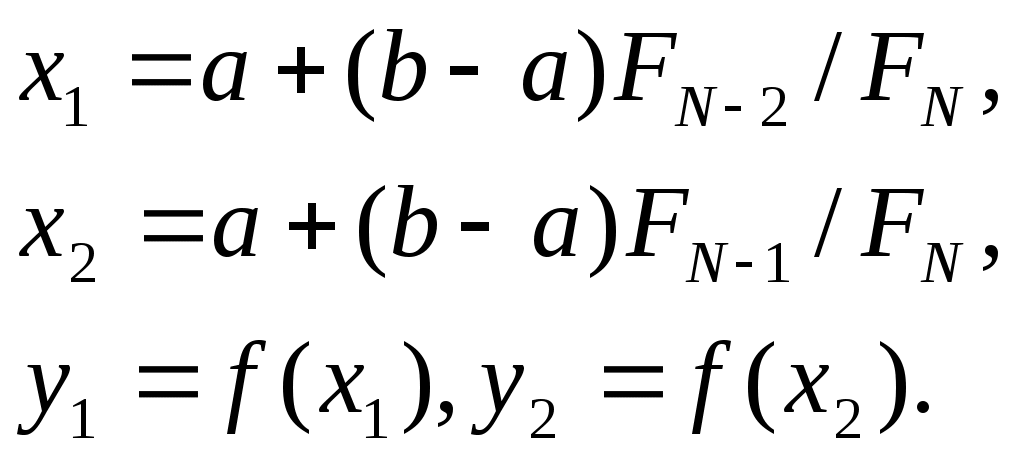. Определяется:



Шаг 2. а) Если y₁≤y₂, то полагают и вычисляют .

б) Если y₁>y₂, то полагают и вычисляют .

Повторить шаг 2 N-2 раза.

Шаг 3. Если y₁2, то полагают и . Если y₁≥y₂, то полагают и .

Закончить поиск.

Длина отрезка неопределённости в методе Фибоначчи .

Метод касательных

Пусть функция f(x) выпукла и дифференцируема на [a,b]. Идея метода состоит в следующем. Пусть [a,b] - отрезок неопределённости и - результаты вычислений в точках a и b. По этой информации строится аппроксимирующая функция, представляющую из себя кусочно-линейную функцию, состоящую из касательной к f(x) в точке a и касательной к f(x) в точке b.

Полученная аппроксимирующая функция есть ломанная состоящая из прямой L_a(x) на [a,c] и L_b(x) на [c,b], где с – точка пересечения касательных. Легко заметить, что при f(a)>0 и f(b)>0 минимум аппроксимирующей функции достигается в точке с. Значение точки пересечения с можно определить по формуле



В точке с производятся вычисления f(c) и f``(c). Если f``(c)=0, то решением задачи будет x^*=c. Если же f `(c)>0, то в качестве следующего отрезка неопределённости будет [a,c]. Если же f``(c)<0, то – отрезок [c,b]. Процесс повторяется до тех пор, пока f `(c)=0 или отр–к неопр–ти не достигнет заданной точности.

Схема алгоритма:

Шаг 1. Заданы a,b,ε. Вычислить .

Шаг 2. Если b-a≤2ε, то полагаем . Поиск окончен. Если b-a>2ε, то вычислить . Если z=0, то полагаем и поиск окончен. Если z<0, то . Если z>0, то . Повт–ть шаг2 .