Алгоритмы цифровой подписи файла RSA, DSA. Алгоритмы цифровой подписи файла rsa, dsa
 Скачать 306.95 Kb. Скачать 306.95 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Пермский национальный исследовательский политехнический университет» Факультет: Прикладной математики и механики Кафедра: Вычислительной математики, механики и биомеханики Направление: 09.03.02 «Информационные системы и технологии» Профиль бакалавриата: «Информационные системы и технологии» КУРСОВАЯ РАБОТА по дисциплине «Информационная безопасность и защита информации» Тема: «Алгоритмы цифровой подписи файла RSA, DSA» Выполнил: студент гр. ИСТ-18-1б а Черных Полина Денисовна т (Ф.И.О.) _______________________ (подпись) Принял: к.т.н., доцент Труфанов А.Н. ______________________________________________________ (должность, ФИО ) ___________ _________________________ (оценка) (подпись) _____________ (дата) Пермь 2021 ОглавлениеВведение 2 Электронная цифровая подпись 4 Хэш-функции 6 Обзор наиболее распространенных ассиметричных алгоритмов ЭЦП 7 Алгоритм цифровой подписи файла RSA 8 Атаки цифровой подписи RSA 9 Алгоритм цифровой подписи файла DSA 10 Оценка скорости алгоритмов RSA и DSA 12 Заключение 14 Список литературы 15 Приложение 1 16 Приложение 2 18 Приложение 3 19 Введение Информация – это один из самых ценных объектов современной жизни. Доступ к информации на сегодняшний день стал простым в связи с появлением глобальных компьютерных сетей. Сегодня большая часть информации, которой обмениваются многие частные лица и организации, представлена в электронном виде. Важно обеспечить защиту электронных данных, также проверить документ на истинность сведений об авторе и на целостность. Эту проблему эффективно решает электронная цифровая подпись. [1] Цифровая подпись файла (далее ЦПФ) – это комплекс мероприятий, который направлен на проверку подлинности и целостности файла после его передачи. ЦПФ может использоваться для проверки безошибочности доставки файла адресату, не была ли потеряна во время передачи какая-либо информация и доставлен ли оригинальный файл без искажений, например, не было ли воздействий на переданный файл со стороны злоумышленников. Недостатком ЦПФ является необходимость надежного хранения своего секретного ключа. ЦПФ включает в себя: Алгоритм генерации ключевых пар пользователя; Функцию вычисления подписи; Функцию проверки подписи. Для подписания и проверки электронной подписи выбраны следующие криптографические алгоритмы: с открытым ключом RSA и DSA, которые имеют существенные различия, рассмотренные в главах. В обоих случаях над содержимым файла вычисляется хеш-функция. Объектом данного исследования является оценка быстродействия работы алгоритмов цифровой подписи файла. Предметом исследования является рассмотрение отдельных вопросов, сформулированных в качестве задач данного исследования. Целью исследования является сравнение двух алгоритмов цифровой подписи файла с точки зрения скорости выполнения. В рамках достижения поставленной цели были поставлены следующие задачи: Изучить теоретические аспекты «Цифровая подпись файла алгоритмом RSA», «Цифровая подпись файла алгоритмом DSA»; Выявить недостатки каждого алгоритма; Провести сравнительный анализ скорости подписи файла и скорости проверки на подлинность двух алгоритов; Электронная цифровая подписьОдной из важных задач криптографии является электронная цифровая подпись. Электронная цифровая подпись (далее ЭЦП) – это информация, которая дополняет электронный документ, подтверждая его подлинность и согласие человека с данными в документе. ЭЦП служит аналогом обычной подписи, которая устанавливает подлинность какого-либо документа или договора. В таблице 1 представлены различия между цифровой и ручной подписями. Таблица 1. Различия цифровой и ручной подписями
Электронная цифровая подпись позволяет осуществить: Контроль целостности; Защиту от подделки документа; Невозможность отказа от авторства; Доказательное подтверждение авторства документа. Перечисленные выше свойства ЭЦП позволяют использовать её для организации юридически значимого электронного документооборота. Целью аутентификации электронных документов является их защита от возможных злоумышленных действий, к которым относятся: активный перехват — нарушитель, подключившийся к сети, перехватывает данные и изменяет их; маскарад — абонент С посылает документ абоненту В от имени абонента А; ренегатство — абонент А заявляет, что не посылал сообщения абоненту В, на деле сообщение было отправлено; подмена — абонент В изменяет или формирует новый документ и заявляет, что получил его от абонента А; повтор — абонент С повторяет ранее переданный документ, который абонент А посылал абоненту В. [2] Эти действия могут нанести ущерб банковским и коммерческим структурам, государственным предприятиям и организациям, частным лицам, которые в своей деятельности применяют компьютерные информационные технологии. Проблему проверки целостности сообщения и подлинности автора сообщения позволяет решить электронная цифровая подпись. Существующие схемы электронной цифровой подписи: Симметричная схема ЭЦП на основе алгоритмов симметричного шифрования. В схеме имеется третье лицо – арбитр, доверием которого пользуются обе стороны. Аутентификацией документа является сам факт его шифрования секретным ключом и передача его арбитру. Используется редко, так как не существует эффективных алгоритмов. Преимуществами симметричной схемы являются: стойкость симметричных схем вытекает из стойкости используемых блочных шифров, надежность которых хорошо изучена; если стойкость шифра недостаточна, шифр можно заменить другим. Недостатками симметричной схемы являются: нужно подписывать отдельно каждый бит информации, что увеличивает подпись (подпись может стать длиннее документа на порядок); сгенерированные для подписи ключи можно использовать только один раз, так как после подписывания половина секретного ключа становится известной. Асимметричная схема ЭЦП на основе алгоритмов асимметричного шифрования. Ассиметричная схема более распространена и широко применяется в криптографии. Если в асимметричных криптосистемах шифрование выполняют на открытом ключе, а дешифрование – на закрытом ключе получателя, то в схемах ЭЦП подпись производится при помощи закрытого ключа, а проверку – с помощью открытого ключа пользователя, который передает сообщение, т.е. схема ЭЦП меняет роли закрытых и открытых ключей. Недостатками ассиметричной схемы являются: асимметричные схемы ЭЦП базируются, как и асимметричное шифрование, на вычислительно сложных задачах дискретного логарифмирования и факторизации; для увеличения криптостойкости необходимо увеличивать длину ключей, это заставляет переписывать программы, реализующие схемы. Также существуют другие алгоритмы цифровых подписей – групповая подпись, неоспоримая подпись, доверенная подпись, слепая подпись.[3] Так как подписываемые документы большого объёма, в схемах ЭЦП подпись ставится не на сам документ, а на его хеш-функцию. Хэш-функцииХэш–функции – это функции, предназначенные для "сжатия" произвольного сообщения, записанного, как правило, в двоичном алфавите, в некоторую битовую последовательность фиксированной длины, называемую сверткой. В криптографии хэш-функции применяются для решения следующих задач: построения систем контроля целостности данных при их передаче или хранении; аутентификация источника данных. При решении первой задачи для каждого набора данных вычисляется значение хеш-функции (называемое кодом аутентификации сообщения), которое передается или хранится вместе с самими данными. При получении данных пользователь вычисляет значение свертки и сравнивает его с имеющимся контрольным значением. Если возникло какое-то несовпадение, значит данные были изменены. При решении второй задачи, аутентификации источника данных, дело ведется с не доверяющими друг другу сторонами. В связи с этим подход, при котором обе стороны обладают одним и тем же секретным ключом не применим. Применяют схемы цифровой подписи, позволяющие осуществить аутентификацию источника данных. Как правило, при этом сообщение, прежде чем быть подписано личной подписью, основанной на секретном ключе пользователя, сжимается с помощью хеш-функции, выполняющей функцию кода обнаружения ошибок. Обозначим через 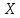 множество, элементы которого являются сообщениями, множество, элементы которого являются сообщениями, 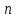 – натуральное число. Хеш–функцией называется легко вычислимая односторонняя функция – натуральное число. Хеш–функцией называется легко вычислимая односторонняя функция 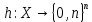 . Ее можно понимать, как отображение из множества сообщений в некоторое подмножество неотрицательных чисел. [4]. . Ее можно понимать, как отображение из множества сообщений в некоторое подмножество неотрицательных чисел. [4]. Использование хэш-функций даёт следующие преимущества: Вычислительная сложность. Обычно хеш цифрового документа делается во несколько раз меньшего объёма, чем объём исходного документа, и алгоритмы вычисления хеша являются быстрыми, чем алгоритмы ЭЦП. Поэтому формировать хэш документ и подписывать его получается намного быстрее, чем подписывать сам документ. Совместимость. Большинство алгоритмов оперирует со строками бит данных, но некоторые используют другие представления. Хеш-функцию можно использовать для преобразования произвольного входного текста в подходящий формат. Целостность. Без использования хеш-функции большой электронный документ в некоторых схемах нужно разделять на достаточно малые блоки для применения ЭЦП. При верификации невозможно определить, все ли блоки получены и в правильном ли они порядке. Стоит заметить, что использование хеш-функции не обязательно при цифровой подписи, а сама функция не является частью алгоритма ЭЦП, поэтому хеш-функция может как использоваться (любая), так и не использоваться. Обзор наиболее распространенных ассиметричных алгоритмов ЭЦПДля генерации пары ключей (секретного и открытого) в ассиметричных алгоритмах ЭЦП используются разные математические схемы, основанные на применении однонаправленных функций. Эти схемы разделяются на две группы. В основе такого разделения лежат известные сложные вычислительные задачи: задача факторизации больших целых чисел; задача дискретного логарифмирования. Алгоритмы ЭЦП подразделяются на цифровые подписи и на цифровые подписи с восстановлением документа. При верификации цифровых подписей с восстановлением документа данные документа восстанавливается автоматически, то есть его не нужно прикреплять к подписи. Обычные цифровые подписи требуют присоединение документа к подписи. К ЭЦП с восстановлением документа относится алгоритм RSA. Схемы цифровой подписи могут быть одноразовыми и многоразовыми. В одноразовых схемах после проверки подлинности подписи необходимо провести замену ключей, в многоразовых схемах это делать не требуется. Алгоритм цифровой подписи файла RSAБезопасность алгоритма электронной подписи RSA основана на трудности задачи разложения на множители. Алгоритм использует два ключа - открытый и закрытый, вместе эти ключи образуют пару ключей. Открытый ключ не требуется скрывать, он используется для зашифровывания данных. Если сообщение было зашифровано открытым ключом, то расшифровать его можно только соответствующим закрытым ключом. RSA может также применяться для того, чтобы подписать и подтвердить сообщение. Схема цифровой подписи меняет роли закрытых и открытых ключей. Первое: используются закрытый и открытый ключи передатчика, а не приемника. Второе: передатчик использует свой собственный закрытый ключ для подписи документа; приемник использует открытый ключ передатчика, чтобы проверить этот документ. Алгоритм подписи RSA с восстановлением сообщения Генерация ключей: Генерация ключей в схеме цифровой подписи RSА точно такая же, как и генерация ключей в криптографической системе RSА. Отправитель выбирает два простых числа 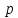 и и 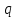 , чтобы не допустить возможности нахождения , чтобы не допустить возможности нахождения 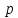 и и 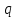 с помощью простого перебора вариантов, эти простые числа должны быть выбраны из достаточно большого множества (т.е. с помощью простого перебора вариантов, эти простые числа должны быть выбраны из достаточно большого множества (т.е. 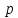 и и 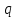 должны быть большими числами и вычисляется модуль этих простых чисел должны быть большими числами и вычисляется модуль этих простых чисел 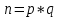 . . Далее отправитель вычисляет значение функции Эйлера от числа 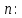 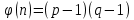 . Выбирается целое число . Выбирается целое число 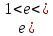 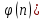 , для открытого ключа взаимно простое со значением функции , для открытого ключа взаимно простое со значением функции 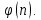 Обычно в качестве Обычно в качестве 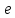 берут простые числа. Вычисляется берут простые числа. Вычисляется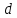 , мультипликативно обратное к числу , мультипликативно обратное к числу 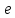 по модулю по модулю 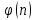 для закрытого ключа, такое, что для закрытого ключа, такое, что 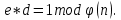 Отправитель сохраняет Отправитель сохраняет 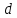 и публично объявляет и публично объявляет 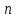 и и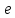 . .Для шифрования данных по открытому ключу 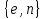 , текст разбивается на блоки, каждый из которых представляется в виде числа , текст разбивается на блоки, каждый из которых представляется в виде числа 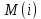 . Обычно блок берут равным одному символу и представляют этот символ в виду числа – его номера в алфавите или кода в таблице символов (например ASCII или Unicode) и данный текст зашифровать по формуле . Обычно блок берут равным одному символу и представляют этот символ в виду числа – его номера в алфавите или кода в таблице символов (например ASCII или Unicode) и данный текст зашифровать по формуле 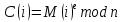 . .Для дешифрования сообщения, используя секретный ключ 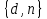 , вычисляется: , вычисляется: 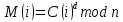 . В результате будет получено множество чисел . В результате будет получено множество чисел 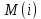 , которые представляют собой исходное сообщение.[5] , которые представляют собой исходное сообщение.[5]Пример: 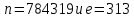 – открытые ключи, – открытые ключи, 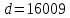 – закрытый ключ. Необходимо передать подписанное сообщение – закрытый ключ. Необходимо передать подписанное сообщение 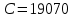 Решение: 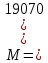 Пара Пара 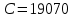 и M = 210625 передается получателю. Для проверки подписи получатель находит на открытом ключе отправителя: и M = 210625 передается получателю. Для проверки подписи получатель находит на открытом ключе отправителя: 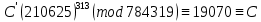 . Подпись законна. Для подписи длинного сообщения его придется разбить на блоки и подписывать каждый блок, что занимает большое количество времени. . Подпись законна. Для подписи длинного сообщения его придется разбить на блоки и подписывать каждый блок, что занимает большое количество времени.Атаки цифровой подписи RSAАтака на основе известного открытого ключа. Перехватив пару 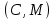 и зная открытый ключ отправителя, криптоаналитик подпирает другое сообщение и зная открытый ключ отправителя, криптоаналитик подпирает другое сообщение 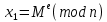 . По сложности решения оно эквивалентно дискретному логарифмированию. . По сложности решения оно эквивалентно дискретному логарифмированию. Атака на основе известных подписанных сообщений Криптоаналитик имеет две пары сообщений 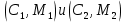 полученные на открытом ключе. Если полученные на открытом ключе. Если 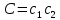 , то , то 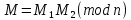 . Криптоаналитик получает новую пару . Криптоаналитик получает новую пару 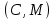 , получатель может посчитать ее, посланной истинным владельцем ключей. Атака называется мультипликативной. , получатель может посчитать ее, посланной истинным владельцем ключей. Атака называется мультипликативной.Атака по выбранным сообщениям Криптоаналитик подбирает два открытых текста 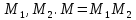 будет текстом для нового документа. Далее криптоаналитик получает подписи у законного отправителя, а потом конструирует пару будет текстом для нового документа. Далее криптоаналитик получает подписи у законного отправителя, а потом конструирует пару 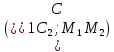 выдавая ее за подписанный документ отправителя. Атака называется селективной, так как создается для заранее подобранного сообщения выдавая ее за подписанный документ отправителя. Атака называется селективной, так как создается для заранее подобранного сообщенияОдин из способов противостоять атакам заключается в том, чтобы подписывать хешированное сообщение и вносить зашумление. Цифровая подпись по схеме RSA С помощью криптографической функции хеширования вычислить хэш сообщения 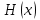 , далее необходимо вычислить подпись , далее необходимо вычислить подпись 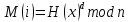 , передать пару , передать пару 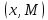 получателю. Для проверки подписи получателем на открытом ключе отправителя необходимо вычислить получателю. Для проверки подписи получателем на открытом ключе отправителя необходимо вычислить 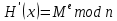 и для переданного сообщения и для переданного сообщения 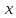 вычислить его хэш вычислить его хэш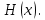 Если Если 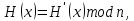 то сообщение верное и подпись закона, в противном случае – подпись не законна. Если криптоаналитик подготовит коллизию то сообщение верное и подпись закона, в противном случае – подпись не законна. Если криптоаналитик подготовит коллизию 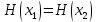 , то он может дать на подпись сообщение , то он может дать на подпись сообщение 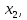 а затем подменить им а затем подменить им 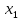 . Составив вместо пары . Составив вместо пары 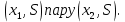 Подмена в схеме цифровой подписи RSA зависит от стойкости алгоритма хеширования к коллизиям. Подмена в схеме цифровой подписи RSA зависит от стойкости алгоритма хеширования к коллизиям.Несколько недостатков алгоритма RSA – при выборе ключей надо проверять дополнительные условия, что сделать затратно. Невыполнение условий делает возможным фальсификацию цифровой подписи со стороны того, кто обнаружит такое невыполнение. Чтобы обеспечить такую же криптостойкость ЭЦП необходимо использовать числа порядка 2512 (или 10154) каждое, это требует больших вычислительных затрат, также ЭЦП RSА уязвима к мультипликативной атаке. Алгоритм цифровой подписи файла DSAСтандарт устанавливает алгоритм DSA цифровой подписи для приложений, которые требуют именно цифровую, а не рукописную подпись. Цифровая подпись DSA – это пара больших чисел, в компьютерном представлении они являются бинарными строками. Для создания цифровой подписи используется закрытый ключ, а для проверки созданной подписи – открытый ключ, который соответствует, но не равен закрытому ключу. Каждая сторона обладает парой открытого и закрытого ключа. Любой может проверить подпись пользователя с использованием открытого ключа данного пользователя. Саму подпись может создать только обладатель закрытого ключа. Подписывается не все сообщение, а дайджест сообщения, который является сжатой версией подписываемых данных – хэш-значение. Дайджест сообщения является входным параметром алгоритма DSA. Цифровая подпись отправляется предназначенному верификатору вместе с подписанными данными (сообщением). Верификатор проверяет подпись сообщения, используя открытый ключ отправителя. Процесс проверки истинности подписи должен использовать ту же хеш-функцию, что и отправитель. Также стоит отметить, что алгоритм RSA не предназначен для шифрования DSA включает в себя два алгоритма (S, V): для создания подписи сообщения (S) и для ее проверки (V). Оба алгоритма изначально вычисляют хеш сообщения, используя определенную хеш-функцию. Алгоритм S использует хеш и секретный ключ для создания подписи, а алгоритм V использует хеш сообщения, подпись и открытый ключ для проверки подписи. В алгоритме подписывается не сообщение, а его хеш, поэтому неизбежны коллизии и одна подпись может быть действительна для нескольких сообщений с одинаковым хешем. Для построения системы цифровой подписи нужно выполнить следующие шаги: Выбор криптографической хеш-функции 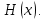 Выбор простого числа 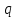 , размерность которого , размерность которого 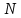 в битах совпадает с размерностью в битах значений хеш-функции в битах совпадает с размерностью в битах значений хеш-функции 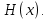 Выбор простого числа 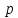 , такого, что , такого, что 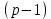 делится на делится на 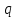 . . Выбор числа 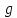 , его мультипликативный порядок по модулю , его мультипликативный порядок по модулю 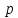 равен равен 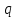 . То есть . То есть 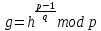 , где , где 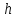 является некоторым произвольным числом является некоторым произвольным числом 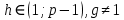 . Обычно . Обычно 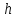 принимают в качестве значения равное 2. принимают в качестве значения равное 2.Секретный ключ представляет собой число 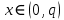 . Открытый ключ вычисляется по формуле . Открытый ключ вычисляется по формуле 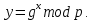 Открытыми параметрами являются числа Открытыми параметрами являются числа 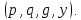 Закрытый параметр только один – число Закрытый параметр только один – число 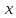 . При этом числа . При этом числа 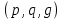 могут быть общими для пользователей, а числа могут быть общими для пользователей, а числа 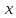 и и 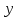 являются закрытым и открытым ключами конкретного пользователя. При подписывании сообщения используются секретные числа являются закрытым и открытым ключами конкретного пользователя. При подписывании сообщения используются секретные числа 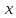 и и 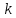 , число , число 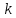 необходимо выбирать случайным образом при вычислении подписи сообщения. необходимо выбирать случайным образом при вычислении подписи сообщения.Подпись сообщения: Выбор случайного числа 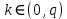 Вычисление 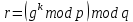 Выбор другого 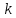 , если , если 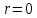 Вычисление 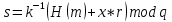 Выбор другого 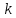 , если , если 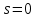 Подписью является пара 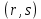 . Вычислительно сложными операциями является возведение в степень по модулю (вычисление { . Вычислительно сложными операциями является возведение в степень по модулю (вычисление {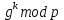 ) и нахождение обратного элемента ) и нахождение обратного элемента 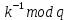 , используя, например, расширенный алгоритм Евклида или малую теорему Ферма в виде , используя, например, расширенный алгоритм Евклида или малую теорему Ферма в виде 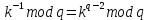 . .Проверка подписи: Вычисление 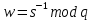 Вычисление 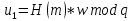 Вычисление 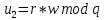 Вычисление 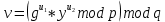 Подпись верна, если 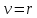 При проверке вычислительно сложные операции это два возведения в степень 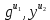 , вычисление хеша , вычисление хеша 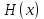 и нахождение обратного элемента и нахождение обратного элемента 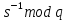 [6]. [6].Пример: 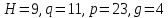 . В качестве секретного ключа . В качестве секретного ключа 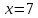 , тогда открытый ключ , тогда открытый ключ 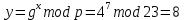 . . Для подписи сообщения: 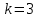 , тогда , тогда 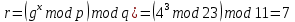 . . 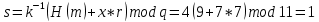 , где учтено, что , где учтено, что 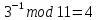 . Подписью является пара числе . Подписью является пара числе 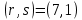 . . Для проверки подписи: 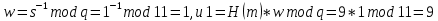 , , 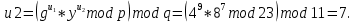 Получили, что Получили, что 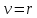 , значит подпись верна , значит подпись вернаАлгоритм DSA имеет следующие основные преимущества: При любом допустимом уровне стойкости, т.е. при любой паре чисел 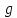 и и 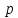 (от 512 до 1024 бит), числа (от 512 до 1024 бит), числа 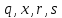 имеют длину по 160 бит, сокращая длину подписи до 320 бит. имеют длину по 160 бит, сокращая длину подписи до 320 бит.Большинство операций с числами 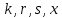 при вычислении подписи производится по модулю числа q длиной 160 бит, что сокращает время вычисления подписи. при вычислении подписи производится по модулю числа q длиной 160 бит, что сокращает время вычисления подписи.При проверке подписи большинство операций с числами 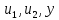 также производится по модулю числа также производится по модулю числа 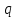 длиной 160 бит, что сокращает объем памяти и время вычисления. длиной 160 бит, что сокращает объем памяти и время вычисления.Недостатком алгоритма DSA является то, что при подписывании и при проверке подписи приходится выполнять сложные операции деления по модулю 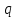 , это не позволяет получать максимальное быстродействие. , это не позволяет получать максимальное быстродействие.Оценка скорости алгоритмов RSA и DSAОба алгоритма RSA и DSA можно использовать для цифровой подписи файла. В качестве оценки скорости работы алгоритма выбирается критерий скорости создания и проверки подписи. Эти два алгоритма имеют различия в исходных файлах: Для создания цифровой подписи применяется один и тот же файл размерностью 962 слова. Алгоритм RSA шифрует данные в другой файл, результатом которого будут определенные цифры, алгоритм DSA, в свою очередь, не требует дополнительного файла, так как не является алгоритмом шифрования. Реализация двух алгоритмов произведена в среде Visual Studio, на языке программирования C#, технология пользовательского интерфейса – Windows Forms. Интерфейс программы находится в Приложение 1. Для начала работы алгоритма необходимо подключить соответствующие файлы. В интерфейсе RSA необходимо указать простые числа 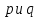 , в дальнейшей оценке , в дальнейшей оценке 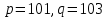 . После подписи файла получен открытый ключ . После подписи файла получен открытый ключ 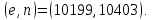 В результате этих действий получено время подписи файла – 0.0530577 мс и время проверки подлинности подписи – 0.0958516 мс. Как видно из результата, скорость проверки подлинности файла происходит медленнее, чем сама подпись. Результаты показаны в Приложение 2на рисунке 4. В результате этих действий получено время подписи файла – 0.0530577 мс и время проверки подлинности подписи – 0.0958516 мс. Как видно из результата, скорость проверки подлинности файла происходит медленнее, чем сама подпись. Результаты показаны в Приложение 2на рисунке 4.Для начала работы алгоритма DSA необходимо подключить файл, который будет подписан цифровой подписью и указать простые числа числа 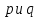 , в дальнейшей оценке , в дальнейшей оценке 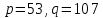 . После подписи файла получен открытый ключ . После подписи файла получен открытый ключ 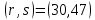 . В результате этих действий получено время подписи файла – 0.0022381 мс и время проверки подлинности подписи – 0.0014511 мс. Как видно из результата, скорость проверки подлинности файла происходит быстрее, чем сама подпись. Результаты показаны в Приложение 2 на рисунке 5. . В результате этих действий получено время подписи файла – 0.0022381 мс и время проверки подлинности подписи – 0.0014511 мс. Как видно из результата, скорость проверки подлинности файла происходит быстрее, чем сама подпись. Результаты показаны в Приложение 2 на рисунке 5.Для наглядности результаты скорости представлены в таблице 2. Таблица 2. Время работы алгоритмов
Исходя из данных в таблице 2 можно сделать вывод о том, что алгоритм DSA цифровой подписи файла работает на порядок быстрее, чем алгоритм шифрования RSA. Это связано с тем, что алгоритм RSA основан на трудности задачи факторизации больших чисел (возведение в степень), в свою очередь, операция деления по модулю  на ЭВМ происходит быстрее. DSA быстрее при генерации ключа, чем RSA. Также меньшая скорость алгоритма RSA связана с тем, что приходится записывать результат шифрования в новый файл и производить из него считывания для проверки подлинности подписи. на ЭВМ происходит быстрее. DSA быстрее при генерации ключа, чем RSA. Также меньшая скорость алгоритма RSA связана с тем, что приходится записывать результат шифрования в новый файл и производить из него считывания для проверки подлинности подписи.Рабочий код программы находится в Приложение 3. ЗаключениеПолитическая, экономическая, юридическая и другие сферы жизни общества в современное время не могут существовать без использования цифровых подписей. Их применение находит место в декларировании товаров, услуг, широко цифровые подписи используются в банковских системах, в электронной торговле и для обычного юридического электронного документооборота. Цифровые подписи файлов реализуются с помощью криптографических алгоритмов. В работе были рассмотрены два разных по своей реализации алгоритма – алгоритм RSA и DSA. Обе эти системы шифрования эффективно используются при создании цифровой подписи данных. Название DSA определяет его основную функцию. Это программа, которая построена для подписания, и поэтому она довольно популярна среди цифровых подписей. RSA включает в себя шифрование и дешифрование содержащегося сообщения, и создание цифровой подписи. Целью исследования являлась сравнительная оценка быстродействия двух алгоритмов, а именно подпись и проверка подписи на подлинность. В результате использования цифровых подписей использование DSA является предпочтительным и работает быстрее на порядок при подписи и проверки подписи на подлинность. Это связано с тем, что DSA быстро создает ключи и не шифрует в последовательность зашифрованное сообщение. Преимуществом RSA является то, что этот алгоритм может использоваться как для шифрования, так и для цифровых подписей, в отличии от алгоритма DSA, который можно использовать только для цифровой подписи. Все поставленные задачи в ходе исследования были выполнены, сравнительный анализ двух алгоритмов проведен. Список литературыЧан Тхюи Зунг. Электронная цифровая подпись файлов PDF // Информационные технологии в науке, управлении, социальное сфере и медицине. – 2015. – С. 229–231. [Электронный ресурс] – Режим доступа: http://yztm.ru/lekc2/l16/ [Электронный ресурс] – Режим доступа: https://articlekz.com/article/32280 Берсенев А.И., Никитенко А.В. Разработка программного обеспечения для создания цифровой подписи на базе алгоритма RSA // Постулат. – 2018. – С. 47. Макаревич А.И., Волошин Д.Д., Протченко Е.Д. Электронная цифровая подпись: суть явления и перспективы развития // Инновации. Наука. Образование. – 2021. – С. 395–399. [Электронный ресурс] – Режим доступа: https://ru.wikipedia.org/wiki/DSA Приложение 1Выбор алгоритма для создания цифровой подписи представлен на рис.1. 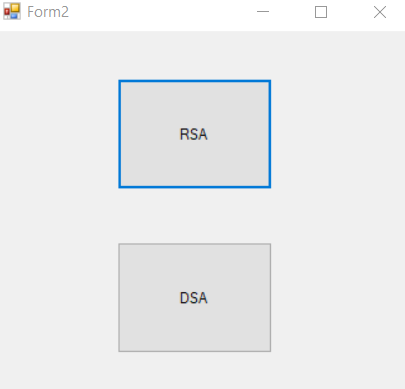 Рис.1. Интерфейс для выбора алгоритма Интерфейс создания и проверки цифровой подписи файла алгоритмом RSA представлен на рисунке 2. 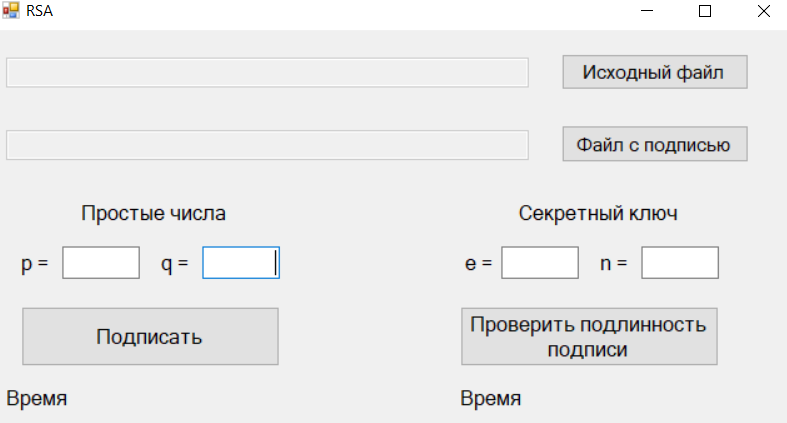 Рис.2. Интерфейс алгоритма RSA Рис.2. Интерфейс алгоритма RSAИнтерфейс создания и проверки цифровой подписи файла алгоритмом DSA представлен на рисунке 3. 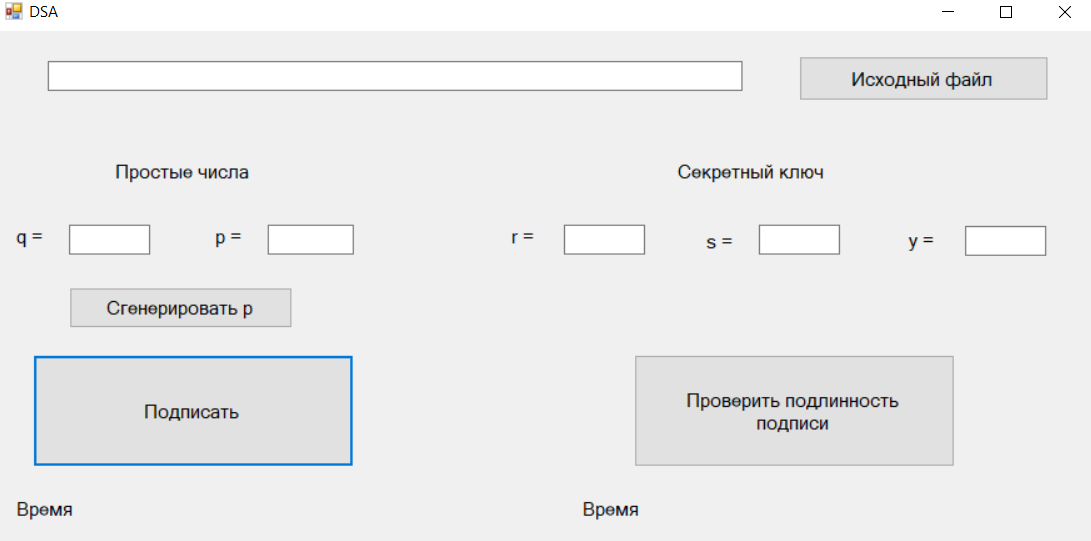 Рис. 3. Интерфейс алгоритма DSA Приложение 2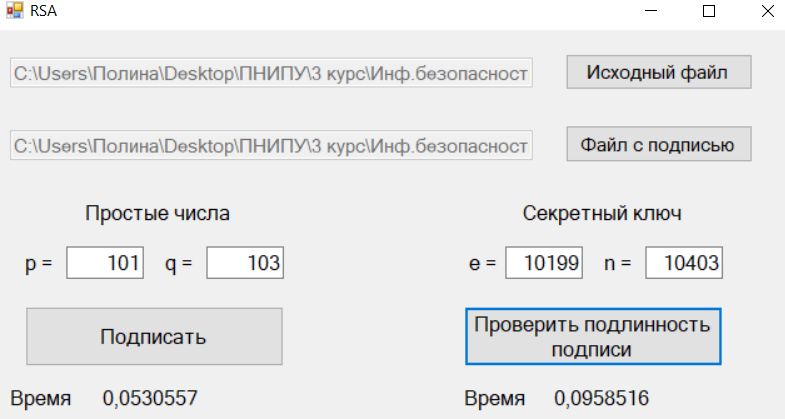 Рис. 4. Время работы алгоритма RSA 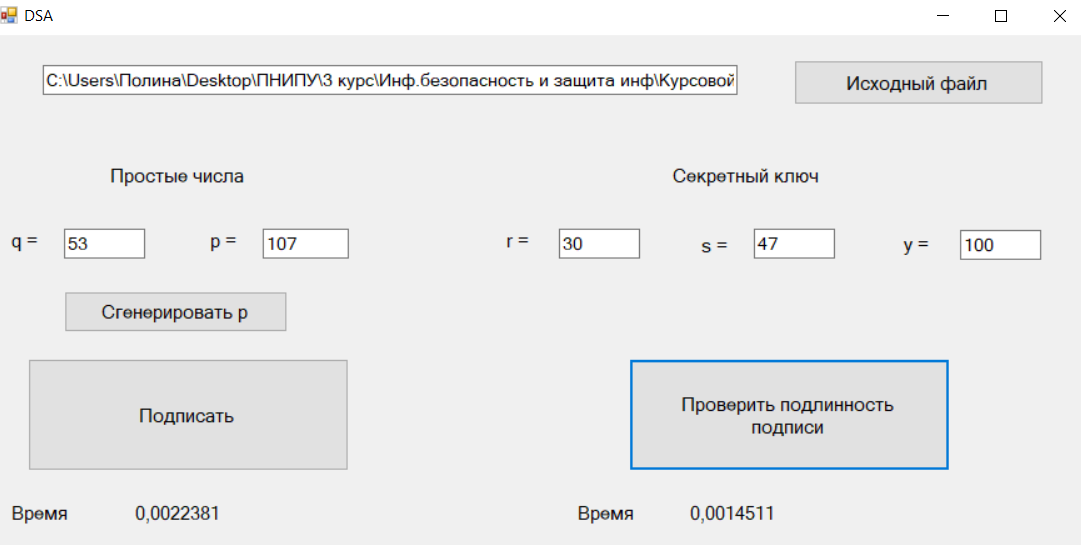 Рис. 4. Время работы алгоритма DSA Приложение 3{ public partial class Form1 : Form { char[] characters = new char[] { '#', '1', '2', '3', '4', '5', '6', '7', '8', '9', '0', '-' }; public Form1() { InitializeComponent(); } //зашифровать private void buttonEncrypt_Click(object sender, EventArgs e) { Stopwatch time = new Stopwatch(); time.Start(); if ((textBox_p.Text.Length > 0) && (textBox_q.Text.Length > 0) && (sourceFilePathTextBox.Text.Length > 0) && (signFilePathTextBox.Text.Length > 0)) { long p = Convert.ToInt64(textBox_p.Text); long q = Convert.ToInt64(textBox_q.Text); if (IsTheNumberSimple(p) && IsTheNumberSimple(q)) { string hash = File.ReadAllText(sourceFilePathTextBox.Text).GetHashCode().ToString(); long n = p * q; long m = (p - 1) * (q - 1); long d = Calculate_d(m); long e_ = Calculate_e(d, m); List StreamWriter sw = new StreamWriter(signFilePathTextBox.Text); foreach (string item in result) sw.WriteLine(item); sw.Close(); textBox_d.Text = d.ToString(); textBox_n.Text = n.ToString(); Process.Start(signFilePathTextBox.Text); } else MessageBox.Show("p или q - не простые числа"); } else MessageBox.Show("Введите p, q, пути к файлам"); time.Stop(); label7.Text = time.Elapsed.TotalSeconds.ToString(); } //расшифровать private void buttonDecipher_Click(object sender, EventArgs e) { Stopwatch time = new Stopwatch(); time.Start(); if ((textBox_d.Text.Length > 0) && (textBox_n.Text.Length > 0) && (sourceFilePathTextBox.Text.Length > 0) && (signFilePathTextBox.Text.Length > 0)) { long d = Convert.ToInt64(textBox_d.Text); long n = Convert.ToInt64(textBox_n.Text); List StreamReader sr = new StreamReader(signFilePathTextBox.Text); while (!sr.EndOfStream) { input.Add(sr.ReadLine()); } sr.Close(); string result = RSA_Dedoce(input, d, n); string hash = File.ReadAllText(sourceFilePathTextBox.Text).GetHashCode().ToString(); time.Stop(); label10.Text = time.Elapsed.TotalSeconds.ToString(); if (result.Equals(hash)) MessageBox.Show("Файл подлинный. Подпись верна."); else MessageBox.Show("Внимание! Файл НЕ подлинный."); } else MessageBox.Show("Введите секретный ключ и пути к файлам."); } //зашифровать private List { List BigInteger bi; for (int i = 0; i < s.Length; i++) { int index = Array.IndexOf(characters, s[i]); bi = new BigInteger(index); bi = BigInteger.Pow(bi, (int)e); BigInteger n_ = new BigInteger((int)n); bi = bi % n_; result.Add(bi.ToString()); } return result; } //расшифровать private string RSA_Dedoce(List { string result = ""; BigInteger bi; foreach (string item in input) { bi = new BigInteger(Convert.ToDouble(item)); bi = BigInteger.Pow(bi, (int)d); BigInteger n_ = new BigInteger((int)n); bi = bi % n_; int index = Convert.ToInt32(bi.ToString()); result += characters[index].ToString(); } return result; } //вычисление параметра d. d должно быть взаимно простым с m private long Calculate_d(long m) { long d = m - 1; for (long i = 2; i <= m; i++) if ((m % i == 0) && (d % i == 0)) //если имеют общие делители { d--; i = 1; } return d; } //вычисление параметра e private long Calculate_e(long d, long m) { long e = 10; while (true) { if ((e * d) % m == 1) break; else e++; } return e; } } } { public partial class Form3 : Form { double g; int y, w, u1, u2, v, s, x, r; int p, q; private void button4_Click(object sender, EventArgs e) { q = Convert.ToInt32(textBox3.Text); p = q + 1; while (true) { bool f = false; for (int i = 2; i < p - 1; i++) { if (p % i == 0) { f = true; break; } } if (!f && (p - 1) % q == 0) { break; } else { p++; } } textBox2.Text = p.ToString(); } private void button1_Click(object sender, EventArgs e) { Stopwatch time = new Stopwatch(); time.Start(); if ((textBox2.Text.Length > 0) && (textBox3.Text.Length > 0) && (textBox1.Text.Length > 0)) { if (num(q)) { int k; Random rand = new Random(); while (g < 1) { g = (Math.Pow(rand.Next(1, p - 1), (p - 1) / q)) % p; } x = rand.Next(0, q); y = fast(Convert.ToInt32(g), x, p); s = 0; r = 0; while (true) { k = rand.Next(0, q); r = fast(Convert.ToInt32(g), k, p) % q; int k1 = 0; while ((k1 * k) % q != 1) { k1++; } s = Convert.ToInt32(k1 * (hash(File.ReadAllText(textBox1.Text), q) + x * r)) % q; if (r != 0 && s != 0) { break; } } textBox6.Text = r.ToString(); textBox7.Text = s.ToString(); textBox8.Text = y.ToString(); } else MessageBox.Show("q - не простое число!"); } else MessageBox.Show("Введите p и q и пути к файлам!"); time.Stop(); label9.Text = time.Elapsed.TotalSeconds.ToString(); } private void button2_Click(object sender, EventArgs e) { Stopwatch time = new Stopwatch(); time.Start(); if (textBox1.Text.Length > 0) { r = Int32.Parse(textBox6.Text); s = Int32.Parse(textBox7.Text); y = Int32.Parse(textBox8.Text); int s1 = 0; while ((s1 * s) % q != 1) { s1++; } w = s1 % q; u1 = (hash(File.ReadAllText(textBox1.Text), q) * w) % q; u2 = (r * w) % q; double mp1 = fast(Convert.ToInt32(g), u1, p); double mp2 = fast(y, u2, p); double res = mp1 * mp2; res %= p; res %= q; v = Convert.ToInt32(res); time.Stop(); label11.Text = time.Elapsed.TotalSeconds.ToString(); MessageBox.Show(v.ToString() + "\n" + r.ToString()); if (v == r) MessageBox.Show("Файл подлинный"); else MessageBox.Show("Файл не подлинный"); } else MessageBox.Show("Введите пути к файлам!"); } } | |||||||||||||||||||||||||||
