Основы дискретно логических систем управления ТП. Фильтрация с 124. Алгоритмы первичной обработки информации в асутп

• Название: Алгоритмы первичной обработки информации в асутп
• Анкор: Основы дискретно логических систем управления ТП
• Дата: 17.09.2022
• Размер: 0.75 Mb.
• Имя файла: Фильтрация с 124.doc
• Тип: Документы; #681392
• страница: 3 из 4

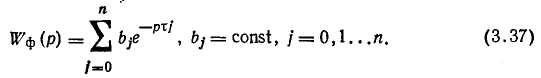Статистический фильтр нулевого порядка. Это простейший среди фильтров данной группы. Его передаточная функция по­лучается из формулы (3.37) при N=0, т. е. это просто усили­тельное звено, выходной сигнал которого



При непосредственном использовании формулы (3.38) сглажен­ная функция г/о (t) будет являться смещенной оценкой полезного сигнала у (t), т. е. ее математическое ожидание не будет равно m_g. Действительно, усредняя левую и правую части (3.38) с уче­том (3.3) и т_е = 0, получим:



Для получения несмещенной оценки к правой части (3.38) необ­ходимо прибавить постоянный член а, удовлетворяющий условию

откуда




Таким образом, формула (4.38) приобретает вид

где 6о — параметр настройки фильтра.

Погрешность! фильтрации, согласно (3.22) и (3.39) с учетом (3.3), равна

о

где y(t)=y(t) —tn(y) —центрированная функция y(t).

Возводя левую и правую части формулы (3.40) в квадрат и усредняя, получим следующее выражение для среднего квадра­та погрешности фильтрации:



Оптимальное значение параметра настройки Ь_о, полученное из необходимого условия минимума функции Б_ф (Ь_о), равно



Ему соответствует минимальная среднеквадратичная погреш­ность гЬи.ттьтпягтии-



Как видно из (3.42), статистический фильтр нулевого порядка

при оптимальной настройке снижает случайную погрешность сигнала измерительной информации в (1+&) раз.

При программной реализации статистического фильтра ну­левого порядка расчёт сглаженных значений производится по формуле:



Статистический фильтр первого порядка. Его передаточную функцию получают из (3.37) при JV = 1:

Во временной области уравнение этого фильтра имеет сле­дующий вид:



Усредняя левую и правую части этого выражения и учиты­вая (3.3), получим: М[у_ф(1)]= (b_o-\-bi)m_y.

Для выполнения условия несмещенности оценки y$(t), т. е. условия M[yy, коэффициенты Ь_о и Ь_и очевидно, должны удовлетворять соотношению Ь\ = \—Ь_о, с учетом которого форму­ла (3.43) приводится к виду:

где Ьо и х — параметры настройки статистического фильтра первого порядка.

Погрешность фильтрации e$(t), согласно (3.3), (3.21) и (3.44), равна



а дисперсия погрешности



Оптимальное значение параметра настройки Ьо получаем из ус-

^ловия _-*г^=0;



В большинстве случаев статистические фильтры реализуют­ся программно, поэтому второй параметр настройки т совпадает с периодом /о квантования по времени функции g(t).

Сравнительный анализ фильтров по совокупности показате­лей (точности, трудоемкости, потребному объему памяти УВМ и др.) показал [24], что для аналогового варианта целесообраз­но использовать экспоненциальный фильтр, а для программной реализации — экспоненциальный или статистический фильтр первого порядка.

3.4. АНАЛИТИЧЕСКАЯ ГРАДУИРОВКА ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ И КОРРЕКЦИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

В метрологии градуировкой называют операцию, с помощью которой делениям шкалы измерительного прибора придают оп­ределенные численные значения, выраженные в единицах изме­рения определяемой величины [27]. Аналогичный смысл вкла­дывают в понятие аналитической градуировки ИП: это опера­ция определения (восстановления) значения х измеряемой вели­чины по сигналу у измерительной информации на выходе ИГГ (см. рис. 3.1). Операцию аналитической градуировки выполняют с использованием градуировочной характеристики ИП, пред­ставляющей собой функцию, обратную его номинальной статиче­ской характеристике (3.2):

где к^т — значение измеряемой величины, соответствующее по градуировоч­ной характеристике ИП значению у сигнала измерительной информации.

Градуировочная характеристика или номинальная статиче­ская характеристика приводится в паспорте ИП в виде аналити­ческой функции или таблицы соответствия значений х^т; и у,-.

Рассмотрим несколько примеров ИП, для которых известно аналитиче­ское выражение характеристики /₀ или /о"¹. Гидростатический уровнемер жидкости преобразует значение измеряемого уровня L в перепад давлений ДР между точками отбора импульсов (в самой нижней _ точке аппарата и над уровнем жидкости):

где р — плотность жидкости, кг/м³; L — уровень жидкости, м; &i—масштаб­ный коэффициент, зависящий от выбора единиц измерения величины ДР (например, если АР выражено в МПа, то £i = 10-⁵).

Перепад ДР линейно преобразуется дифманометром в стандартный электрический сигнал у (например, 0—10 В на весь диапазон измерения). Таким образом, статическая характеристика данного ИП описывается урав­нением



где kz=y*l&P* — коэффициент усиления дифманометра; у*—значение вы­ходного сигнала дифманометра, соответствующее верхнему пределу измере­ния ДР* (для упрощения выкладок предполагается, что нижним пределом измерений является нуль).





Ей соответствует градуировочная характеристика:




Номинальную статическую характеристику получают из (3.49) при номи­нальном значении плотности p=po=const:

Для комплекта рН-метра, состоящего из чувствительного элемента и преобразователя э. д. с. чувствительного элемента в стандартный электри­ческий сигнал, статическая характеристика описывается уравнением [2]

тде £_и, рН_и, So и а — константы, значения которых зависят от типа элект­родов чувствительного элемента; 9 — температура анализируемого раствора, "С; й₃=




Ей соответствует градуировочная характеристика





Номинальная статическая характеристика расходомера переменного пе­репада давления описывается следующей нелинейной функцией:




Номинальную статическую характеристику рН-метра получают из (3.51) при номинальном значении температуры 9₀=20°С:

где у — стандартный выходной сигнал дифманометра (который рассматри­вается как линейный преобразователь перепада давления на сужающем устройстве в выходной сигнал у); k — коэффициент, зависящий от условий измерения; Q — измеряемая величина, т. е. объемный расход потока через сечение трубопровода.

Ей соответствует градуировочная характеристика



где ko —■ градуировочное значение коэффициента k.

Если градуировочная характеристика ИП задана аналити­чески, то операция аналитической градуировки сводится к вы­полнению расчета по формуле (3.47).



коэффициенты a_v которого определяют по методу наименьших квадратов, т. е. из условия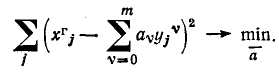



Для многих ИП с нелинейной градуировочной характеристи­кой последнюю определяют экспериментально и вносят в пас­портные данные в виде графика или таблицы соответствия зна­чений х^т и г//. В частности, в виде таблицы задают градуировоч-ные характеристики наиболее массовых ИП, применяемых в АСУТП химических производств — термопреобразователей со­противления (ТС) и термоэлектрических преобразователей тем­пературы (ТПТ). При табличном представлении градуировоч­ной характеристики применяют способ аналитической градуи­ровки, заключающийся в аппроксимации табулированной градуи­ровочной характеристики аналитическим выражением, которое в дальнейшем используют для вычисления значений х^г. Чаще всего в качестве аппроксимирующей функции используют мно­гочлен m-й степени:
Например, слабо нелинейные градуировочные характеристики ТС и ТПГ с достаточно высокой точностью аппроксимируются полиномами не выше третьей степени. В частности, градуировочная характеристика хромель-копе-левого ТПТ в диапазоне температур 0—600 ^СС аппроксимируется следую­щим полиномом второй степени [45]:

где х^с — значение температуры, °С; у — э. д. с. ТПТ, мВ. Максимальная от­носительная погрешность аппроксимации табличных данных не превыша­ет 0,5%.

Вычисления по формуле (3.53) целесообразно выполнять по так называемой схеме Горнера:

Блок-схема алгоритма, реализующего вычисление по схеме Горнера, представлена на рис. 3.10.

Операция аналитической градуировки ИП позволяет опреде­лить действительное значение х измеряемой величины по сигна­лу у измерительной информации только в том случае, если х преобразовано в у в соответствии с номинальной статической характеристикой ИП (3.2), т. е. при выполнении условия



Действительно, в этом случае



Однако в производственных условиях невозможно стабилизиро­вать значения всех влияющих величин на номинальном уровне, что приводит к нарушению условия (3.54). При этом



где Д£—■ вектор отклонений влияющих величин от номинальных значений.

Возникает так называемая дополнительная погрешность измере­ния, которая, очевидно, равна:



Если известна полная статическая характеристика ИП (3.1) и вектор Az, можно рассчитать погрешность Ах^г и внести соответ­ствующую поправку к расчетному значению х^г, полученному по градуировочной характеристике.

Истинное значение х при нарушении условия (3.54) находят при расчете по функции, обратной полной статической характе­ристике ИП:



Его можно найти, умножая значение х^т, полученное по форму­ле (3.47), на некоторый поправочный коэффициент k_n:



Откуда с учетом (3.56) и (3.47) получим:





В качестве примера найдем выражение для расчета поправочного коэф­фициента для гидростатического уровнемера. Статическую характеристику (3.49) гидростатического уровнемера преобразуем так, чтобы сделать явной ее зависимость от температуры жидкости, которая является главной влияю­щей величиной. Для этого заменим плотность р соотношением, описываю­щим ее зависимость от температуры 6 при небольших отклонениях от номи­нального значения 6о:

где р — температурный коэффициент объемного расширения жидкости. По­сле подстановки (3.59) в (3.49) получим полную статическую характери­стику в виде



Обратная ей функция:

Поправочный коэффициент найдем, согласно (3.58), делением этого выра­жения на градуировочную характеристику (3.50):

Особенно часто в АСУТП корректируют результаты измере­ния расходов, поскольку обычно их используют для расчета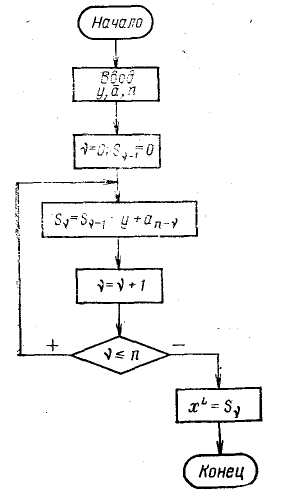


Рис. 3.10. Блок-схема алгоритма вычис лення полинома по схеме Горнера

fexHHKO-экономических показателен производства. В подавляющем боль­шинстве случаев расход газов, пара и жидкости, транспортируемых пс трубопроводам, измеряют с по­мощью расходомеров переменногс перепада давления [27]. При ис пользовании стандартных сужаю­щих устройств расходомеры этогс типа градуируют расчетным путем т. е. для определенных номинальны? условий измерения (температура давление и т. д.) рассчитывают гра дуировочную характеристику расхо домера. Коррекцию измеренных зна чений расхода производят при от клонении условий измерения от но минальных, а также с целью приве дения результатов к единым услови

ям (обычно температура 20 °С, давление 10⁵ Па), чтобы сделать их сопоставимыми.

. Для коррекции применяют общие соотношения (3.57) и (3.58). Формулы для расчета поправочных коэффициентов для разных возможных на практике случаев измерения расхода по­лучают подстановкой в (3.58) выражения (3.52), конкретизиро­ванного для каждого случая.

Для примера рассмотрим коррекцию результатов измерения массового расхода насыщенного пара на изменение давления в трубопроводе. В этом случае функция, обратная полной статической характеристике расходомера, описывается выражением [27].



где k — коэффициент, практически не зависящий от давления; р — плот­ность измеряемой среды.








Таким образом, £п=Ур/ро- В частности, для диапазона давлений 0,25— 0,85 МПа зависимость р от давления насыщенного пара аппроксимируется полиномом второй степени [45]:

Для насыщенного пара плотность зависит от давления, поэтому попра­вочный коэффициент получаем делением выражения (3.60) на градуировоч-ную характеристику (3.52), которую запишем в виде:

Задав номинальное значение Яо, можно по этой формуле рассчитать ро, а затем в процессе измерения рассчитывать фактическую плотность, соответ­ствующую текущему значению Р, и вносить поправку на изменение условий.

3.5. КОНТРОЛЬ И ПОВЫШЕНИЕ ДОСТОВЕРНОСТИ ИСХОДНОЙ ИНФОРМАЦИИ

Исходная информация о текущем состоянии объекта управле­ния поступает в УВМ по многим десяткам, а иногда и сотням ИИК. С увеличением их числа возрастает риск попадания в сис­тему недостоверной информации, поэтому одной из важнейших функций первичной обработки информации в АСУТП является контроль ее достоверности.

Недостоверная исходная информация появляется при отказах ИИК, которые делятся на полные и частичные (метрологичес­кие). Полный отказ наступает при выходе из строя ИП или по­вреждении линии связи ИП с УВМ. При частичном отказе тех­нические средства сохраняют работоспособность, однако по­грешность измерения соответствующего параметра превышает допустимое значение.

Обнаружение полных отказов ИИК является гораздо более простой задачей, чем выявление частичных отказов. Поэтому сначала рассмотрим алгоритмы контроля достоверности исход­ной информации, позволяющие обнаружить только полный от­каз ИИК. При этом недостоверное значение параметра должно быть заменено достоверной оценкой, в качестве которой может