Основы дискретно логических систем управления ТП. Фильтрация с 124. Алгоритмы первичной обработки информации в асутп

• Название: Алгоритмы первичной обработки информации в асутп
• Анкор: Основы дискретно логических систем управления ТП
• Дата: 17.09.2022
• Размер: 0.75 Mb.
• Имя файла: Фильтрация с 124.doc
• Тип: Документы; #681392
• страница: 2 из 4

Для оценки погрешности экстраполяции можно использовать выражение (3.15) с заменой в нем ^о на i_g.

Линейная интерполяция (рис. 3.7) является простейшим ме­тодом интерполяции, в основе которого лежит кусочно-линейная аппроксимация функции g(t) на интервале значений jto<-t<£

<(/+1)*о.

Уравнение прямой, проходящей через точки g(jto) и ё{(/+1)^о]. можно записать в виде:




Погрешность линейной интерполяции

Подставляя в это выражение значение г/ф(О из формулы (3.16), возводя его в квадрат и усредняя по множеству интервалов, а затем по т в пределах от 0 до to, получаем выражение для дис­персии погрешности линейной интерполяции:



В литературе описаны и другие, более сложные методы ин­терполяции и экстраполяции [24], однако на практике их при­меняют редко. Современные УВМ обеспечивают достаточно вы­сокую частоту опроса ИИК, поэтому обычно удается обеспе­чить требуемую точность восстановления измеряемых величин, используя простейший метод ступенчатой экстраполяции. Обыч­но среди десятков и даже сотен ИИК можно выделить несколь­ко групп параметров, близких по частотным спектрам. Тогда можно выбрать общий период опроса для каждой группы дат­чиков. Например, в производстве разбавленной азотной кислоты опрос группы датчиков, контролирующих малоинерционный про­цесс контактного окисления аммиака, проводится с периодом 15 с, а опрос датчиков на инерционном процессе абсорбции — с периодом 2 мин.

Выбор частоты опроса измерительных преобразователей через число нулей случайного процесса. Выбор частоты опроса t₀ по формуле (3.15) требует знания корреляционной функции R_s(r) случайного процесса g(t). Для получения оценки корреляцион­ной функции необходим значительный объем вычислений. Кро­ме того, часто проще и естественнее задать не дисперсию ошиб­ки Д» от замены непрерывного случайного процесса ступенча­тым, а отношение этой величины к дисперсии случайного про­цесса D. Учтем также важность гарантии того, что выбранная частота опроса не приведет к появлению большей относитель­ной погрешности, чем заданное значение, т. е. важно получить оценку сверху для периода опроса t₀.

Для решения поставленной задачи воспользуемся неравен­ством [22]:



Если бы продолжительность корреляционной функции можно было оценить без построения этой функции, то неравенство (3.17) позволило бы оценить интервал опроса /₀- Ниже получим оцен­ку величины А через среднее число нулей случайного процесса No, т. е. через среднее число пересечений им линии своего ма­тематического ожидания в единицу времени. Предварительно отметим, что рассмотрение процессов с корреляционной функ­цией конечной продолжительности более естественны, чем про­цессов со спектральной плотностью, ограниченной частотой среза, так как первые, в отличие от вторых, физически реали­зуемы.

Известна связь среднего числа нулей N_o со спектральной плотностью случайного процесса 5(ш):



Пользуясь этой формулой, попытаемся найти минимальную продолжительность корреляционной функции R_g, имеющей за­данное число нулей N_o. В силу свойств преобразования Фурье, произведение любых двух функционалов, однозначнскопределяе-мых корреляционной функцией R_g, один из которых имеет раз­мерность времени, а другой — частоты [последний выражается через преобразование Фурье от R_g(r)], не изменяется при сжа­тии или растяжении корреляционной функции, т. е. при измене­нии масштаба времени.

Анализ размерности правой части формулы для iV₀² показы­вает, что среднее число нулей имеет размерность частоты. В ка­честве функционала, имеющего размерность времени, примем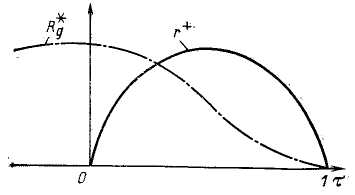



Рис. 3.8. Определение корреляци­онной функции минимальной про­должительности

продолжительность А кор­реляционной функции R_g (t). Таким образом, произведе­ние C=NqA зависит от фор-

мы R_g(x) и не зависит от выбора масштаба времени. Поэтому первоначально зафиксируем /А=1 и при этом условии будем-искать минимум N_o, а точнее JV₀². Чтобы учесть требование ко­нечной продолжительности корреляционной функции, перейдем во временную область. Представим 5(ю) в виде |s(«o) |², что соответствует представлению Rg(x) как свертки двух функций — г⁺(х) и /"(т), первая из которых определена на интервале (О, 1), а вторая — на интервале (0, —1). Формула для среднега числа нулей может быть теперь переписана в виде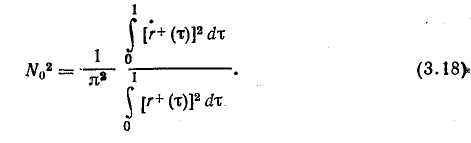


Чтобы найти минимум N\ потребуем, как обычно, минимума числителя при фиксированном значении знаменателя. Задача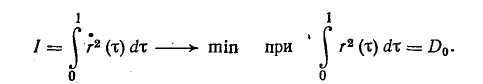



(индекс «+» для краткости записи опущен) решается с испольг-зованием уравнения Эйлера. Составим функционал Лагранжа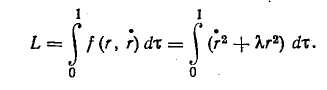



и запишем для него уравнение Эйлера


Его решение (а точнее — множество решений):



Подставив решение в условие для заданной дисперсии, получим-A²_Q=D₀/n.

Величина / на найденных решениях /=£>₀&²я²; тогда I/D₀=kn². Это отношение минимально для k = l. Соответствующее решение

т+(т) показано на рис. 3.8. Там же нанесена корреляционная функция R_g*(x), имеющая при заданном среднем числе нулей минимальную продолжительность.

При Д=1 величина С_тщ оказывается равной единице. Следо­вательно, если фиксировано среднее число нулей No, то мини­мальная продолжительность корреляционной функции Amm=l/Af₀.





Пример. Пусть относительная дисперсия, связанная с дискретностью опроса датчиков, не должна превышать пяти процентов. По формуле (3.19) имеем для t₀ оценку




Возвращаясь к неравенству (3.17) и подставляя вместо Д значение Amm, получим оценку сверху для интервала опроса:

Для получения N_o определяют среднее значение случайного процесса, выбирают реализацию такой длины, чтобы случайный процесс пересекал линию среднего значения приблизительно 100 раз, и подсчитывают отношение числа пересечений к длине реализации: No=N(T)/T.

Если число пересечений в точности равно 100, то, обозначив соответст­вующую продолжительность реализации через Г_1Оо, получим:



Таким образом, на реализации длиной Тюо нужно 500 раз отобрать по­казания измерительного преобразователя.

3.3. ФИЛЬТРАЦИЯ ИЗМЕРЯЕМЫХ ВЕЛИЧИН ОТ ПОМЕХ

Фильтрацией называют операцию выделения полезного сигнала измерительной информации y(t) из его суммы с помехой e(t) (см. рис. 3.1). Обычно методы фильтрации основаны на разли­чии частотных спектров функций y(t) и e(t): как правило, поме­ха бывает более высокочастотной. Для выполнения дальнейших выкладок примем следующие допущения:

1) функция y(t) является стационарным случайным процес­сом с известными статистическими характеристиками — матема­тическим ожиданием М_у, дисперсией D_y и автокорреляционной функцией, описываемой следующим выражением:



2) помеха e(t) также является стационарным случайным процессом, некоррелированным с полезным сигналом y(t); для нее известны статистические характеристики М_е = 0, D_e = kD_y:



В результате фильтрации получают оценку г/_ф (г) сигнала из­мерительной информации, к которой предъявляют следующие требования:

она должна быть несмещенной, т. е. должна удовлетворять условию



среднеквадратичная погрешность оценки должна быть мини­мальна, т. е.

Оценку уф(t) будем рассматривать как выходной сигнал ли­нейного динамического звена — фильтра с АФХ №ф(т), на вход которого поступает выходной сигнал ИИК g(t) =y(t)-{-e(t).

В разд. 1.5 сформулирована общая задача синтеза линейно­го оптимального фильтра и получены выражения для АФХ иде­ального (нереализуемого) и физически реализуемого фильтров. Однако синтез оптимального реализуемого фильтра является сложной задачей и, кроме того, требует достаточно точного за­дания характеристик полезного сигнала и помехи. Поэтому на практике обычно ограничиваются так называемым параметри­ческим синтезом фильтров, т. е. задают структуру функции Т^Ф^'со), а ее параметры определяют из условий (3.22) и (3.23).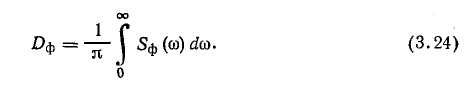




Спектральную плотность функции e$(t) рассчитывают по формуле



Расчет дисперсии погрешности фильтрации обычно выпол­няют в частотной области, используя выражение

Функции S_e(co) и S_y (ю) являются спектральными плотностями сигналов e(t) и у (t), которые получают в результате преобразо­вания по Фурье автокорреляционных функций (3.20) и (3.21):



На практике применяют несколько простых алгоритмов филь­трации, рассмотренных ниже. Следует отметить, что в АСУТП некоторые методы фильтрации могут осуществляться как аппа-ратурно (с использованием специальных аналоговых устройств), так и программно. Поэтому для каждого такого метода фильт­рации изложен аналоговый и дискретный варианты реализации. Экспоненциальный фильтр*. В аналоговом варианте экспонен-

Н азвание фильтра обусловлено тем, что импульсная характеристика апериодического звена описывается экспоненциальной функцией.
циальный фильтр представляет собой апериодическое звено и описывается дифференциальным уравнением



где у и &ф — параметры настройки фильтра. Уравнению (3.28) соответствует АФХ



где Гф=1./7 — постоянная времени фильтра.

Из условия (3.22) для статического режима определяют оп­тимальное значение параметра k& (коэффициента усиления):



Определение оптимального значения параметра у произво­дится из условия (3.23), для чего предварительно рассчитывают спектральную плотность погрешности экспоненциального филь­тра по формуле (3.25) с учетом (3.29) и (3.30):



Дисперсия погрешности экспоненциального фильтра, согласно (3.24) —(3.25) с учетом (3.29), равна



При вычислении этого интеграла оба слагаемых подынтеграль­ного выражения раскладывают на простые дроби, каждая из которых сводится к табличному интегралу вида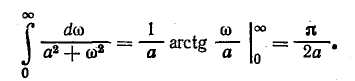



После выполнения соответствующих преобразований полу­чают следующее выражение для дисперсии погрешности филь­трации:



■Оптимальное значение параметра настройки у получают из не­обходимого условия экстремума функции Aj>(y)^:



откуда



Таким образом, функция О_ф(у) имеет единственную точку стационарности, тип которой зависит от знака второй произ­водной при v=Y°- Можно показать, что при выполнении условия



особая точка является минимумом функции Aj>(y)> а при выпол­нении условия kmy=Y° функция D&(y) достигает максимума. Таким образом, если сочетание характеристик по­лезного сигнала и помехи соответствует случаю (3.32а),то опти­мальное значение параметра настройки определяется по форму­ле (3.32). Если это условие не выполняется, то оптимальным является наибольшее допустимое значение параметра у.

При программной реализации экспоненциального фильтра дифференциальное уравнение (3.28) заменяют разностным урав­нением вида



где / — номер цикла расчета.

Отсюда получают следующее рекуррентное соотношение для вычисления сглаженного значения г/ф(/) в очередном /-том цикле

ПЯГЦЙТЯ¹



К достоинствам алгоритма экспоненциальной фильтрации отно­сятся малая трудоемкость расчетов и малый объем памяти УВМ, в которой должна храниться величина у и обновляемая в каждом цикле расчета величина г/ф(/—1).

Фильтр скользящего среднего в аналоговом варианте реализует вычисление среднего значения функции g(t)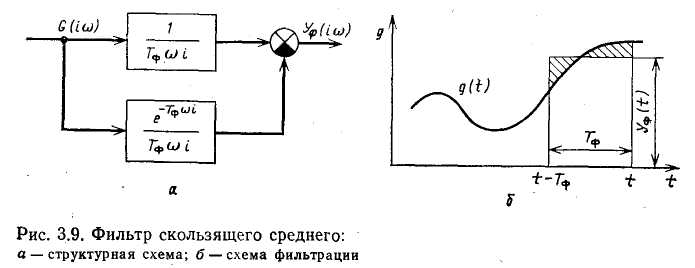



на интервале времени от t—Гф до t (рис. 3.9,6):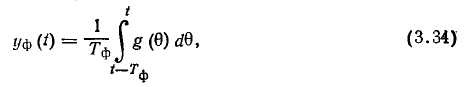



где Гф — параметр настройки фильтра (время усреднения).

Преобразуем правую часть выражения (3.34), представив

РГП R RH7ie^%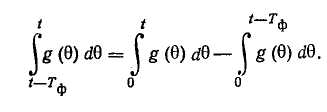



Отсюда видно, что фильтр скользящего среднего представляет собой параллельное соединение двух интегрирующих звеньев, одно из которых последовательно соединено со звеном запазды­вания (рис. 3.9а). Поэтому амплитудно-фазовая характеристи­ка фильтра описывается выражением



которое аналогично по структуре выражению (3.12) и может быть преобразовано к виду



Решая совместно (3.24) — (3.27) и (3.35), можно получить выражение для дисперсии погрешности А}> фильтра скользяще­го среднего и определить оптимальное значение Г°ф параметра настройки из необходимого условия минимума функции />ф(Г_ф). Получаемое при этом выражение очень громоздко, неудобно для практического использования. На его основе рассчитаны номо­граммы [24], по которым для заданных значений а, т, k можно определить 7"^о_ф.

При программной реализации фильтра скользящего средне­го расчет сглаженного значения #ф(/) в очередном /-том цикле проводится по формуле

А7



где N=T
Для расчета по формуле (3.36) требуется хранить в памяти УВМ (N-\-l) значение функции g(jt₀).

Статистические фильтры. Статистическими называют фильтры, которые в аналоговом варианте представляют собой параллель­ное соединение (я+1) цепочек, состоящих из усилительного зве-

на и звена чистого запаздывания. Передаточная функция такого фильтра