Основы дискретно логических систем управления ТП. Фильтрация с 124. Алгоритмы первичной обработки информации в асутп

• Название: Алгоритмы первичной обработки информации в асутп
• Анкор: Основы дискретно логических систем управления ТП
• Дата: 17.09.2022
• Размер: 0.75 Mb.
• Имя файла: Фильтрация с 124.doc
• Тип: Документы; #681392
• страница: 4 из 4

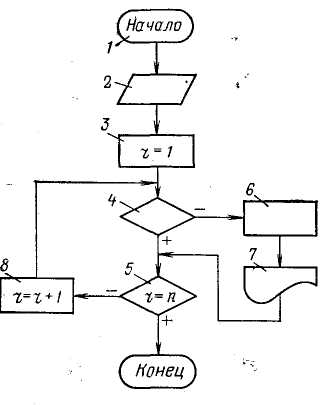Рис. 3.11. Блок-схема алгоритма допус-кового контроля достоверности исходной информации

быть использовано предыдущее достоверное значение этого пара­метра или его значение, усред­ненное за некоторый интервал времени, предшествующий мо­менту обнаружения отказа ИИК. Последний способ применяют для наиболее ответственных парамет­ров, например, расходов, значе­ния которых используют при рас­чете ТЭП.

Алгоритм допускового контроля параметра. Он основан на том, что при работе объекта значения

каждого из контролируемых технологических параметров дс,- не могут выходить за определенные границы:

Соответственно при исправном ИИК должен быть ограничен и сигнал измерительной информации г/,, поступающий в УВМ по этому каналу:

Контроль достоверности по этому алгоритму заключается в про­верке выполнения условия (3.61) для каждого значения сигна­ла измерительной информации, поступившего при очередном опросе ИИК. Блок-схема алгоритма представлена на рис. 3.11. Он работает следующим образом.

После инициации работы алгоритма (блок /) и ввода исход­ных данных (блок 2) организуется цикл проверки ИИК, каждо­му из которых присвоен свой номер г (блок 3); в блоке 4 прове­ряется условие (3.61), при выполнении которого проверяется ус­ловие окончания работы алгоритма (блок 5). Выполнение усло­вия г = п (где п — число контролируемых ИИК) останавливает работу алгоритма. Если это условие не выполняется, счетчик но­мера ИИК увеличивается на 1 (блок 8), и цикл повторяется. Если при проверке в блоке 4 условие (3.61) не выполняется, то в блоке 6 недостоверное значение y_r (jt₀) заменяется достовер­ным значением yj[(j—1)^₀] того же сигнала, полученным в пре­дыдущем цикле опроса ИИК. Затем на печать выводится сооб­щение о том, что обнаружен отказ t-того ИИК (блок 7), и рабо­ту алгоритма продолжает блок 5.

Этот алгоритм применим не только для стационарных про­цессов, но и для нестационарных, например периодических. В этом случае граничные значения у,* и у,* в условии (3.61) являются не константами, а функциями времени, отсчитываемо­го от начала процесса. Алгоритм допускового контроля скорости изменения сигнала

измерительной информации основан на том, что скорость изме­нения любого технологического параметра х_г ограничена усло­вием


где о)с—частота среза функции x_r(t)\ x, — среднее значение этой функции.

Соответственно должна быть ограничена и скорость измене­ния сигнала измерительной информации y_r(t)




Контроль достоверности по данному алгоритму заключается в проверке выполнения условия (3.63), причем оценку производ­ной dyijdt рассчитывают по формуле



Контроль достоверности исходной информации по условиям (3.61) и (3.63) часто совмещается. Тогда в блок-схему алгорит­ма на рис. 3.11 между блоками 4 и 5 вводится еще один блок, осуществляющий проверку выполнения условия (3.63). При на­рушении этого условия инициируется блок 6.

Алгоритмы контроля достоверности исходной информации, е помощью которых выявляются частичные отказы ИИК, основаны на использовании информационной избыточности, которая всег­да имеется в АСУТП. Избыточность прежде всего может быть создана искусственно при проектировании АСУТП за счет ап-' паратурной избыточности, например резервирования ИИК для контроля наиболее важных технологических параметров.

Другой вид информационной избыточности в АСУТП обусг ловлен тем, что информация о действительном значении некото­рого технологического параметра содержится не только в изме­ренном значении этого параметра, но и в измеренных значениях других параметров, связанных с ним устойчивыми зависимостя­ми, например, уравнениями материального баланса.

При разработке алгоритмов контроля достоверности исход­ной информации на основе информационной избыточности при­нимают следующие допущения:

1) маловероятно одновременное появление в пределах рас­сматриваемой структуры более чем одного источника недосто­верной информации;

2. 
   маловероятно одновременное изменение характеристик двух независимых источников информации, при котором соот­ ношение между ними остается неизменным;
   
3. 
   маловероятен выход за допустимые пределы показателя, зависящего от нескольких независимых величин, при нормаль­ной вариации последних.
   

Алгоритмы, применяемые при аппаратурном резервировании И И К. Эти алгоритмы используют сигналы измерительной ин­формации j/_v, полученные в результате преобразования одной измеряемой величины с помощью п ИП, так что v=l,2,...п.

Если я>3 и погрешности ИП близки друг к другу, то опре­деление частичного отказа ИИК производится по нарушению условия


где у — среднее значение i/v; с=const — наибольшее допустимое значение модуля разности у\ и у; величина с может быть принята равной (2—3) а, где а — среднеквадратичная погрешность ИП.

Важное практическое значение имеет случаи, когда один из параллельных ИИК можно принять за эталонный, поскольку его погрешность существенно меньше, чем у других. В этом слу­чае признаком частичного отказа v-ro ИИК является нарушение условия



где c_v = (2—3)ct_v—допустимая погрешность v-ro ИИК; 0"v — среднеквадра­
тичная погрешность v-ro ИИК. J

Разновидностью данного алгоритма является метод тестовых (калиброванных) сигналов, позволяющий контролировать ис­правность ИИК без ИП. Метод заключается в том, что ИП на время отключают и вместо него к входу ИИК подключают источ­ник тестового сигнала, для которого с высокой точностью извест­но значение у_э- Если сигнал y_v на выходе проверяемого ИИК удовлетворяет условию (3.65), то канал признают исправным; его нарушение является признаком частичного отказа.

Если п = 2 и погрешности обоих ИИК близки, то признаком частичного отказа одного из них может служить нарушение ус­ловия:



При этом невозможно определить отказавший ИИК без привле­чения дополнительной информации.

Алгоритмы, использующие связи между измеряемыми величина­ми. Эти алгоритмы широко применяют для контроля достовер­ности исходной информации и диагностики частичных отказов ИИК. При этом связи могут быть функциональными (например, уравнения материального и энергетического баланса) или веро­ятностными. В последнем случае они описываются регрессион­ными уравнениями.

Рассмотрим общую методику контроля достоверности резуль­татов измерения п величин, связанных т уравнениями вида


Будем считать, что заданы функции f,(x) и дисперсии а<² погрешностей измерения, которые являются случайными вели­чинами с нормальным законом распределения и нулевым мате­матическим ожиданием.

Уравнения (3.66) выполняются только при подстановке в них истинных значений Xi измеряемых величин. Если же значе­ния измеряемых величин известны с погрешностями Д#,-, т. е.


то при их подстановке функции f/(x) не равны нулю:



где // — погрешность выполнения /-го уравнения связи (3.66), вызванная по­грешностями измерения.

Функции fi(x) обычно являются непрерывными и дифферен­цируемыми по всем аргументам, поэтому их можно разложить в ряд Тейлора по степеням величин А*,-: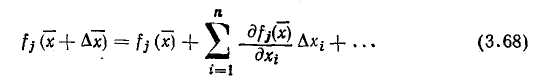

Поскольку при частичных отказах ИИК погрешности Axi малы, можно не принимать во внимание нелинейные члены ряда (3.68), содержащие в качестве сомножителей величины высших поряд­ков (Ах)^к, где k = 2,3,.... Тогда с учетом (3.66) из (3.68) полу­чим:


Подстановка уравнения (3.69) в (3.67) дает:




где

На практике расчет параметров ац проводят, используя не ис­тинные, а измеренные значения xi, так что



Система уравнений



является линеаризованной математической моделью объекта уп­равления или некоторой его части. Она служит для расчета оценок погрешностей А*,-, которые используют при контроле достоверности исходной информации и диагностике частичных отказов ИИК.

Метод расчета погрешностей Ах,- зависит от соотношения между числом измеряемых величин п и числом уравнений свя­зи т.

При п = т значения Axi определяют одним из численных ме­тодов решения системы т линейных уравнений (3.72). При л>т можно попытаться уменьшить число рассчитываемых оце­нок погрешностей с п до т. Для этого результаты измерений q = n—т параметров следует заранее рассматривать как досто­верные. Если такое допущение правомерно, задача сводится к рассмотренному выше варианту.

В общем случае при п>т оценки погрешностей Ax_h опреде­ляют, решая оптимизационную задачу



при выполнении соотношений (3.70). Весовые коэффициенты р₍-, позволяющие учесть различие в классе точности ИП, рассчиты­вают по формулам [24]

п



где £=const, oi — среднеквадратичная погрешность i-того ИП.

Для решения задачи нелинейного программирования (3.73) используют метод неопределенных множителей Лагранжа. Сос­тавляют функцию Лагранжа:



где X, = const — множители Лагранжа.

Для нее записывают необходимые условия оптимальности

—з— = 0 и-^г- =0 в виде следующей системы (п-\-т) уравне-

OXi OAj

ний: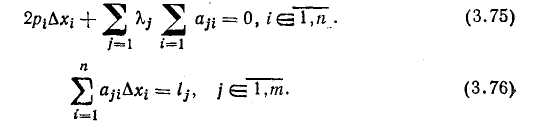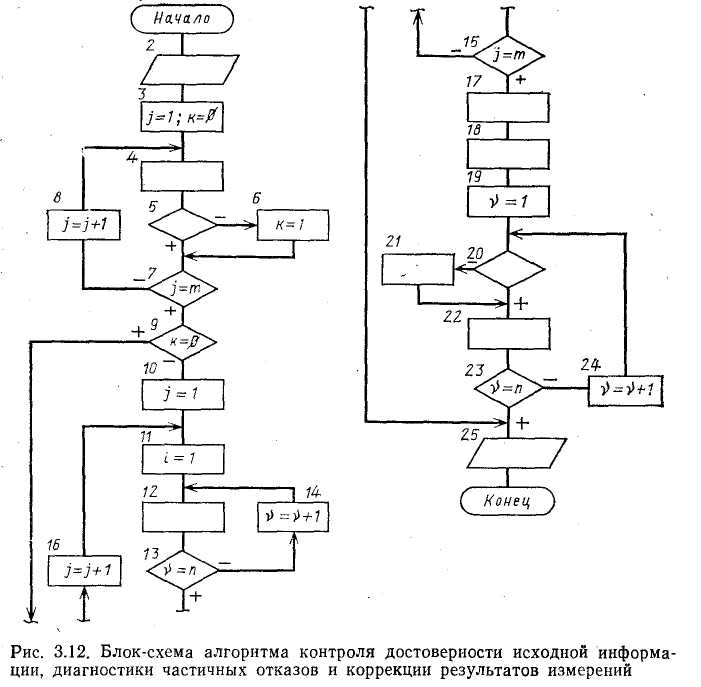





Искомые оценки погрешностей Axi являются решениями систе­мы линейных уравнений (3.75) — (3.76).

Рассчитанные значения оценок погрешностей используют для коррекции результатов измерений:

Xi = xi—Axi. (3.77)

Среднеквадратичная погрешность откорректированных зна­чений измеренных величин меньше среднеквадратичной погреш­ности измерений ИИК, причем увеличение точности оценок тем значительнее, чем меньше разность п—т.

На рис. 3.12 представлена блок-схема алгоритма контроля достоверности исходной информации, диагностики частичных отказов ИИК и коррекции результатов измерений, основанного на использовании функциональных связей между измеряемыми величинами. Он работает следующим образом.

После инициации (блок /) в оперативную память УВМ вво­дятся исходные данные (блок 2) и начинается циклический рас-

чет погрешностей // уравнений связи по формуле (3.67), для че­го служат блоки 4, 7 и 8. В блоке 5 рассчитанные значения срав­ниваются с наибольшими допустимыми значениями /_;*:

Если условие (3.78) выполняется для всех уравнений связи, то все результаты измерения признают достоверными, т.е. х, = л;,-, и работа алгоритма заканчивается, тах как логическая перемен­ная k сохраняет свое первоначальное значение k = 0.

Нарушение условия (3.78) хотя бы для одного уравнения связи служит признаком наличия частичных отказов. При этом в блоке 6 логическая переменная k приобретает значение 1, и после окончания цикла расчета погрешностей I] уравнений связи алгоритм переходит к расчету оценок Axt погрешностей измере­ний (блоки 10—25). Он начинается с циклического вычисления оценок коэффициентов а/,- линеаризованных уравнений связи в блоках 10—16. Коэффициенты рассчитываются по формуле (3.71) в блоке 12. В блоке 17 формируется матрица коэффици­ентов a,i системы линейных уравнений (3.72) и матрица-столбец погрешностей //. Если расчет выполняется для случая п = т, то на этом работа блока 17 заканчивается. Для случая п>т мат­рица, формируемая блоком 17, дополняется строками, соответ­ствующими уравнениям (3.75).

Блок 18 предназначен для решения одним из численных ме­тодов системы линейных уравнений (3.72) или (3.75) — (3.76). Эта часть алгоритма требует основных затрат машинного вре­мени и оперативной памяти ЭВМ. В результате работы блока 18 получают оценки погрешностей измерений Ах,-.

В блоках 19—23 производится диагностика частичных отка­зов ИИК, для чего оценки Axt сравнивают с наибольшими до­пустимыми значениями погрешностей измерений Ах₍*:



Нарушение условия (3.79), которое проверяется в блоке 20, является признаком частичного отказа t-того ИИК; сообщение об этом формируется блоком 21. В блоке 22 рассчитывается откорректированное значение Xi измеряемой величины по фор­муле (3.77). Блок 25 служит для вывода результатов расчета, после чего работа алгоритма завершается. Исходными данными для работы алгоритма являются массивы следующих величин: измеренных значений параметров хг, допустимых погрешностей /,•* уравнений связи; допустимых погрешностей А*,-* измерений; весовых коэффициентов р,- (если п>от).

Пример. Рассмотрим контроль достоверности результатов измерения расходов азотной кислоты, поступающей с производства на склад. Производство состоит из трех параллельно работающих агрегатов. На выхо­де каждого из них измеряется расход q_t (г'еТГЗ) продукционной кислоты. Затем кислота поступает в коллектор, в котором измеряется общий расход <74. Поскольку расход q_t является одним из основных отчетных параметров производства, для его измерения используют расходомер более высокого класса точности, чем для измерения расходов q\ — q% Исходные данные для алгоритма контроля достоверности исходной информации следующие:

измеренные значения параметров *i= 12,1 т/ч; х₂= 11,6 т/ч; £₃=12,4 т/ч; 2₄=34,5 т/ч;

допустимая погрешность выполнения уравнения связи 2*= 1,5 т/ч;

допустимые погрешности измерения отдельных параметров Ax_t* = &.x₂* = = Д*з*=0,45 т/ч; Д*₄*=0,65 т/ч;

среднеквадратичные погрешности измерения 01 = 0,3 т/ч; 02=0,2 т/ч; сг₃= = 0,35 т/ч; о₄=0,33 т/ч.

Действуем в соответствии с блок-схемой на рис. 3.12.

1. Определим погрешность / выполнения уравнения связи между изме­ряемыми параметрами, которое в данном случае имеет вид:

2. 
   Проверка условия (3.78) приводит к выводу, что среди результатов,
   измерения Xi имеются недостоверные.
   
3. 
   Исходное уравнение (3.80) является линейным, следовательно, коэф­
   фициенты линеаризованного уравнения (3.70) совпадают с коэффициентами
   уравнения (3.80):
   

Для дальнейшего формирования системы уравнений (3.75) — (3.76) не­обходимо рассчитать весовые коэффициенты pi. Запишем условие (3.74) для заданных значений ы: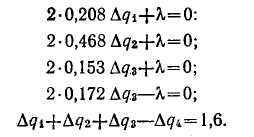

откуда £=0,0187; pi = 0,208; р₂=0,468; р₃=0,153; р₄=0,172. Теперь запишем систему уравнений (3.75) —(3.76):

Ее решениями являются следующие значения оценок погрешностей изме­рений:

4. Проверим выполнение условия (3.79). Как легко убедиться, оно не выполняется только для параметра <7з, из чего следует вывод о частичном отказе этого ИИК.

В заключение рассчитаем откорректированные оценки значений измеряе­мых величин:

<7i=ll,701 т/ч; ?2=11,423 т/ч; <7з=П,858 т/ч; «74=34,982 т/ч. При этих значениях удовлетворяется уравнение связи (3.80).

Изложенный выше алгоритм можно использовать не толь­ко для определения частичных отказов ИИК, но и для более глубокой диагностики погрешностей измерения. Для этого под­вергают статистической обработке расчетные значения погреш­ностей Axi, получаемые в последовательных циклах работы алгоритма. Оценка математического ожидания случайной вели-

чины Axi за N циклов расчета характеризует систематическую погрешность измерения t-того ИИК: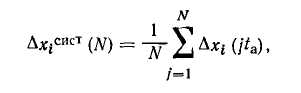



где t_a — период, с которым выполняются расчеты по алгоритму контроля до­стоверности исходной информации.

По формуле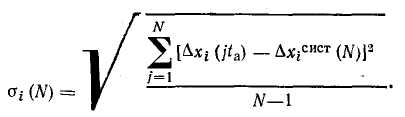



рассчитывают оценку среднеквадратичной погрешности изме­рения.