Алгоритмизации

• Название: Алгоритмизации
• Дата: 27.09.2022
• Размер: 1.15 Mb.
• Имя файла: 12_100229_1_124427 (1).docx
• Тип: Документы; #700459
• страница: 36 из 67

Бинарныедеревья

Бинарное дерево – это динамическая структура данных, в которой ка- ждый узел-родитель содержит, кроме данных, не более двух сыновей (левый и правый).

На рисунке приведен пример бинарного дерева (корень обычно изображается сверху, хотя изображение можно и перевернуть).

Корень дерева

Root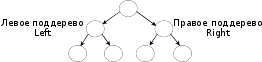


Такая структура данных организуется следующим образом (N– NULL):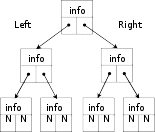





Высота дерева, как и раньше, определяется количеством уровней, на которых располагаются его узлы.

Если дерево организовано таким образом, что для каждого узла все ключи его левого поддерева меньше ключа этого узла, а все ключи его

правого поддерева – больше, оно называется деревом поиска. Одинаковые ключи здесь не допускаются.

Представление динамических данных в виде древовидных структур оказывается довольно удобным и эффективным для решения задач быстрого поиска информации.

Сбалансированными, или AVL-деревьями, называются деревья, для каждого узла которых высóты его поддеревьев различаются не более чем на

1. 
   Причем этот критерий обычно называют AVL-сбалансированностью в отличие от идеальной сбалансированности, когда для каждого узла дерева количество узлов в его левом и правом поддеревьях различаются не более чем на единицу [44].
   

Дерево по своей организации является рекурсивной структурой данных, поскольку каждое его поддерево также является деревом. В связи с этим действия с такими структурами чаще всего описываются с помощью рекурсивных алгоритмов.

2. Основныеалгоритмыработысбинарнымдеревом

В общем случае при работе с такими структурами необходимо уметь:

• 
  построить (создать) дерево;
  
• 
  вставить новый элемент;
  
• 
  обойти все элементы дерева, например, для просмотра или выполнения некоторой операции;
  
• 
  выполнить поиск элемента с указанным значением в узле;
  
• 
  удалить заданный элемент.
  

Обычно бинарное дерево строится сразу упорядоченным, т.е. узел левого сына имеет значение меньшее, чем значение родителя, а узел правого сына– большее.

3. Формированиедерева

Например, имеется последовательность ключей 17, 18, 6, 5, 9, 23, 12, 7, 8, тогда построенное по ним дерево будет выглядеть следующим образом: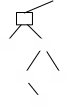

2: 6<17

6

1: 18>17

18

3: 5<17, 5<6

4: 9<17, 9>6

5: 23>17, 23>18

7: 7<17, 7>6, 7<9 6: 12<17, 12>6, 12>9


7


12




8: 8<17, 8>6, 8<9, 8>7