Алгоритмизации

• Название: Алгоритмизации
• Дата: 27.09.2022
• Размер: 1.15 Mb.
• Имя файла: 12_100229_1_124427 (1).docx
• Тип: Документы; #700459
• страница: 35 из 67

Алгоритмвставкиэлементавсписокпослеэлементас указанным ключом

Вставить в список элемент после элемента, значение информационной части (ключ) которого совпадает со значением, введенным с клавиатуры.

Решение данной задачи проводится в два этапа – поиск и вставка.

Первый этап аналогичен рассмотренному в алгоритме удаления, а второй проводится только при условии, что искомый элемент найден, т.е. указатель на него key не равен NULL.

Этапвторой– вставка

1. 
   Захватываем память под новый элемент
   

t = (Spis*) malloc(sizeof(Spis));

2. 
   Формируем информационную часть: scanf(“%d”, &t -> info);
   
3. 
   Связываем новый элемент с предыдущим
   

t -> Prev = key;

4. 
   Связываем новый элемент со следующим
   

t -> Next = key -> Next;

5. 
   Связываем предыдущий элемент с новым
   

key -> Next = t;

6. 
   Если элемент добавляется не в конец списка (как показано на схеме ниже), т.е. key != end, то
   

( t -> Next ) -> Prev = t;

7. 
   Иначе, еслиkey= end, то указательkey->NextравенNULL(в п. 4
   

установлено окончание списка) и новым последним становится t

end = t;

Общая схема вставки элемента: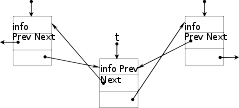

key

key->Next

. . .

. . .

Алгоритмосвобожденияпамяти,занятойсписком, аналогичен рассмотренному алгоритму для стека (см. разд. 15.2).

5. Нелинейныеструктурыданных

В предыдущих разделах мы рассмотрели линейные структуры динамических списковых данных.

Введение в динамическую переменную двух и более полей-указателей позволяет получить нелинейные структуры данных. Наиболее распространенными являются структуры с иерархическим представлением, которые хорошо изображаются следующим образом: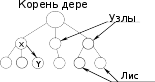




Такая конструкция данных получила название «дерево».

Дерево состоит из элементов, называемых узлами(вершинами). Узлы соединены между собой направленными дугами. В случае X→Y вершина X называется родителем, а Y – сыном (дочерью).

Дерево имеет единственный узел, не имеющий родителей (ссылок на этот узел), который называется корнем. Любой другой узел имеет ровно одного родителя, т.е. на каждый узел дерева имеется ровно одна ссылка.

Узел, не имеющий сыновей, называется листом.

Внутреннийузел – это узел, не являющийся ни листом, ни корнем.

Порядок узла равен количеству его узлов-сыновей. Степень дерева– максимальный порядок его узлов. Высота(глубина)узларавна числу его родителей плюс один. Высотадерева – это наибольшая высота его узлов.