Алгоритмизации
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
Алгоритм,использующийстекПолучение обратной польской записи с использованием стека может осуществляться весьма просто на основе алгоритма, предложенного Дейкстрой, который ввел понятие стекового приоритета операций:
Суть алгоритма в следующем. Просматривается исходная строка символов Sслева направо, операнды переписываются в выходную строку В, а знаки операций заносятся в стек, который первоначально пуст, на основе следующих правил: если в строке Sвстретился операнд, то помещаем его в строку В; если в Sвстретилась открывающая скобка, то помещаем ее в стек; если в Sвстретилась закрывающая скобка, то выталкиваем из стека в строку В все операции до открывающей скобки, саму отрывающую скобку также извлекаем из стека; обе скобки (открывающая и закрывающая) игнорируются; если в S встретилась операция Х, то выталкиваем из стека все операции, приоритет которых не ниже Х, после чего операцию Хзаписываем в стек; при достижении конца строки S, если стек не пуст, переписываем его элементы в выходную строку В. Обратная польская запись обладает рядом замечательных свойств, которые превращают ее в идеальный промежуточный язык при трансляции. Во-первых, вычисление выражения, записанного в обратной польской записи, может проводиться путем однократного просмотра, что является весьма удобным при генерации объектного кода программ. Например, вычисление полученного выражения (15.1) может быть проведено следующим образом:
Здесь R1 и R2 – вспомогательные переменные. ПримерреализацииПусть задано выражение a+b*c+(d*e+f)*g. Необходимо записать это выражение в постфиксной форме. Правильным ответом будет выражение abc*+de*f+g*+. Решаем эту задачу, используя стек. Пусть исходная информация хранится в строке S=”a+b*c+(d*e+f)*g”. Результат будем получать в строке В. Начинаем последовательно просматривать символы исходной строки, причем стек пуст и В – пустая строка. Букву «a» помещается в строку В, а операцию«+» помещаем в стек. Букву «b» помещаем в строку В. На этот момент стек и строка В выглядят следующим образом: В= ”ab” Операцию «*» помещаем в стек, т.к. элемент в вершине стека имеет более низкий приоритет. Букву «с» помещаем в строку В, после чего имеем
”abс” Следующий символ строки S«+». Анализируем стек и видим, что элемент в вершине стека «*» и следующий за ним «+» имеют приоритеты не ниже текущего, следовательно, обе операции извлекаем из стека и помещаем в строку В, а текущий элемент помещаем в стек. В итоге имеем В= ”abс*+” Далее в строке Sследует символ «(», его помещаем в стек, а букву «d» помещаем в строкуВ, в результате получается
”abс*+d” Следующий в строке S символ «*». Так как открывающую скобку нельзя извлечь из стека до тех пор, пока не встретилась закрывающая, то «*» помещаем в стек. Букву «e» помещаем в строку В:
”abс*+de” Следующий прочитанный символ «+», и т.к. элемент стека «*» имеет более высокий приоритет, то извлекаем его из стека и помещаем в строку В, а текущий символ «+» помещаем в стек. Символ «f» помещаем в строкуВ:
”abс*+de*f” Далее в строке S идет закрывающая скобка, все элементы стека до символа «)» помещаем в строку В(это элемент «+»), а сам символ «(» извлекаем из стека. Обе скобки игнорируются: В= ”abс*+de*f+” Операцию «*» помещаем в стек, а букву «g» – в строку В:
”abс*+de*f+g” Все символы строки S рассмотрены, следовательно, анализируем состояние стека, если он не пуст, то переписываем все его элементы в строку В:  В= ”abс*+de*f+g*+” В= ”abс*+de*f+g*+”Таким образом, просмотрев исходную информацию только один раз, мы решили поставленную задачу. Текст программы, реализующий рассмотренный алгоритм, может иметь следующий вид: . . . struct Stack { char c; // Символ операции Stack *Next; } ; int Prior (char); Stack* InS( Stack*,char); Stack* OutS( Stack*,char*); void main () { Stack *t, *Op = NULL; // Стек операций Op– пуст char a, In[50], Out[50]; // Входная Inи выходная Outстроки int k = 0, l = 0; // Текущие индексы для строк puts(" Input formula : "); gets(In); while ( In[k] != '\0') { // Анализируем символы строки In // Если символ «)», выталкиваем из стека в выходную строку все операции if ( In[k] == ')' ) { while ( (Op -> c) != '(' ) { // до открывающей скобки Op = OutS(Op,&a); // Считываем элемент из стека if ( !Op ) a = '\0'; Out[l++] = a; // и записываем в строку Out. } t = Op; // Удаляем из стека открывающую скобку Op = Op -> Next; free(t); } // Если символ строки In– буква, заносим ее в строку Out if ( In[k] >= 'a' && In[k] <= 'z' ) Out[l++] = In[k]; // Если символ – открывающая скобка, записываем ее в стек if ( In[k] == '(' ) Op = InS(Op,In[k]); /* Если символ – знак операции, переписываем из стека в строку Outвсе операции с большим или равным приоритетом*/ if ( In[k] == '+' || In[k] == '–' || In[k] == '*' || In[k] == '/' ) { while ( Op != NULL && Prior (Op -> c) >= Prior (In[k]) ) { Op = OutS(Op,&a); // Извлекаем из стека символ Out[l++] = a; // и записываем в строку Out } Op = InS(Op,In[k]); // Текущий символ – в стек } k++; } // Конец цикла анализа входной строки // Если стек не пуст, переписываем все операции в выходную строку while ( Op !=NULL) { Op = OutS(Op,&a); Out[l++] = a; } Out[l] = '\0’; printf("\n Polish = %s", Out); // Выводим на экран результат } //======= Функция реализации приоритета операций ========= int Prior ( char a ) { switch ( a ) { case '*': case '/': return 3; case '–': case '+': return 2; case '(': return 1; } return 0; } // ============== Добавление элемента в стек ============= Stack* InS( Stack *t, char s) { Stack *t1 = (Stack*) malloc(sizeof(Stack)); t1 -> c = s; t1-> Next = t; return t1; } // ============== Извлечение элемента из стека=============== Stack* OutS( Stack *t, char *s ) { Stack *t1 = t; *s = t -> c; t = t->Next; free(t1); return t; } ПонятиехешированияДля решения задачи поиска необходимого элемента среди данных большого объема был предложен алгоритм хеширования (hashing– перемешивание), при котором создаются ключи, определяющие данные массива и на их основании данные записываются в таблицу, названную хеш- таблицей. Ключи для записи определяются при помощи функции i = h(key), называемой хеш-функцией. Алгоритм хеширования определяет положение искомого элемента в хеш-таблице по значению его ключа, полученного хеш- функцией. Понятие хеширования–это разбиение общего (базового) набора уникальных ключей элементов данных на непересекающиеся наборы с определенным свойством. Возьмем, например, словарь или энциклопедию. В этом случае буквы алфавита могут быть приняты за ключи поиска, т.е. основным элементом алгоритма хеширования являетсяключ(key). В большинстве приложений ключ обеспечивает косвенную ссылку на данные. Фактически хеширование – это специальный метод адресации данных для быстрого поиска нужной информации по ключам. Если базовый набор содержит Nэлементов, то его можно разбить на 2 N различных подмножеств. Хеш-таблицаихеш-функцииФункция, отображающая ключи элементов данных во множество целых чисел (индексы в таблице – хеш-таблица), называется функцией хеширования, илихеш-функцией: i= h(key); где key– преобразуемый ключ, i– получаемый индекс таблицы, т.е. ключ отображается во множество целых чисел (хеш-адреса), которые впоследствии используются для доступа к данным. Однако хеш-функция для нескольких значений ключа может давать одинаковое значение позиции iв таблице. Ситуация, при которой два или более ключа получают один и тот же индекс (хеш-адрес), называется коллизиейпри хешировании. Хорошей хеш-функцией считается такая функция, которая минимизирует коллизии и распределяет данные равномерно по всей таблице, а совершенной хеш-функцией – функция, которая не порождает коллизий: (key) Хеш аблица   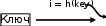 i i. . . 0 1 ...  m mРазрешить коллизии при хешировании можно двумя методами: методом открытой адресации с линейным опробыванием; методом цепочек. Хеш-таблицаХеш-таблица представляет собой обычный массив с необычной адресацией, задаваемой хеш-функцией. Хеш-структурусчитают обобщением массива, который обеспечивает быстрый прямой доступ к данным по индексу. Имеется множество схем хеширования, различающихся как выбором удачной функцииh(key), так и алгоритма разрешения конфликтов. Эффективность решения реальной практической задачи будет существенно зависеть от выбираемой стратегии. Примерыхеш-функцийВыбираемая хеш-функция должна легко вычисляться и создавать как можно меньше коллизий, т.е. должна равномерно распределять ключи на имеющиеся индексы в таблице. Конечно, нельзя определить, будет ли некоторая конкретная хеш-функция распределять ключи правильно, если эти ключи заранее не известны. Однако, хотя до выбора хеш-функции редко известны сами ключи, некоторые свойства этих ключей, которые влияют на их распределение, обычно известны. Рассмотрим наиболее распространенные методы задания хеш-функции. Метод деления. Исходными данными являются – некоторый целый ключ keyи размер таблицы m. Результатом данной функции является остаток от деления этого ключа на размер таблицы. Общий вид функции: int h(int key, int m) { return key % m; // Значения } Дляm= 10 хеш-функция возвращает младшую цифру ключа. Х ш таблица (m=10)
   Х ш адреса i: Х ш адреса i: key= 342 key= 756 Коллизия  key= 55556 key= 55556Для m= 100 хеш-функция возвращает две младшие цифры ключа. Хеш аблица ( 100)
   Х -адреса i: Х -адреса i: key= 3402 key= 7597 Коллизия  key= 55597 key= 55597Аддитивныйметод, в котором ключом является символьная строка. В хеш-функции строка преобразуется в целое суммированием всех символов и возвращается остаток от деления на m (обычно размер таблицы m = 256). int h(char *key, int m) { int s = 0; while(*key) s += *key++; return s % m; } Коллизии возникают в строках, состоящих из одинакового набора символов, например, abc и cab. Данный метод можно несколько модифицировать, получая результат, суммируя только первый и последний символы строки-ключа. int h(char *key, int m) { int len = strlen(key), s = 0; if(len < 2) // Если длина ключа равна0 или1, s = key[0]; // возвратить key[0] else s = key[0] + key[len–1]; return s % m; } В этом случае коллизии будут возникать только в строках, например, abcи amc. Методсерединыквадрата, в котором ключ возводится в квадрат (умножается сам на себя) и в качестве индекса используются несколько средних цифр полученного значения. Например, ключом является целое32-битное число, а хеш-функция возвращает средние 10 бит его квадрата: int h(int key) { key *= key; key >>= 11; // Отбрасываем11 младших бит return key % 1024; // Возвращаем 10 младших бит } Метод исключающего ИЛИ для ключей-строк (обычно размер таблицы m=256). Этот метод аналогичен аддитивному, но в нем различаются схожие слова. Метод заключается в том, что к элементам строки последовательно применяется операция «исключающее ИЛИ». В мультипликативном методе дополнительно используется случайное действительное число r из интервала [0,1), тогда дробная часть произведенияr*keyбудет находиться в интервале[0,1]. Если это произведение умножить на размер таблицы m, то целая часть полученного произведения даст значение в диапазоне от 0 до m–1. int h(int key, int m) { double r = key * rnd(); r = r – (int)r; // Выделили дробную часть return r * m; } В общем случае при больших значениях m индексы, формируемые хеш-функцией, имеют большой разброс. Более того, математическая теория утверждает, что распределение получается более равномерным, если m является простым числом. В рассмотренных примерах хеш-функция i= h(key) только определяет позицию, начиная с которой нужно искать (или первоначально – поместить в таблицу) запись с ключом key. Поэтому схема хеширования должна включать алгоритм решения конфликтов, определяющий порядок действий, если позиция i = h(key) оказывается уже занятой записью с другим ключом. СхемыхешированияВ большинстве задач два и более ключей хешируются одинаково, но они не могут занимать в хеш-таблице одну и ту же ячейку. Существуют два возможных варианта: либо найти для нового ключа другую позицию, либо создать для каждого индекса хеш-таблицы отдельный список, в который помещаются все ключи, преобразованные в этот индекс. Эти варианты и представляют собой две классические схемы: хеширование методом цепочек (со списками), или так называемое многомерное хеширование – chaining with separate lists; хеширование методом открытой адресации с линейным опробыванием – linear probe open addressing. Методоткрытойадресациислинейнымопробыванием.Изначально все ячейки хеш-таблицы, которая является обычным одномерным массивом, помечены как не занятые. Поэтому при добавлении нового ключа проверяется, занята ли данная ячейка. Если ячейка занята, то алгоритм осуществляет осмотр по кругу до тех пор, пока не найдется свободное место («открытый адрес»), т.е. либо элементы с однородными ключами размещают вблизи полученного индекса, либо осуществляют двойное хеширование, используя для этого разные, но взаимосвязанные хеш-функции. В дальнейшем, осуществляя поиск, сначала находят по ключу позицию iв таблице, и, если ключ не совпадает, то последующий поиск осуществляется в соответствии с алгоритмом разрешения конфликтов, начиная с позицииi по списку. Метод цепочек используется чаще предыдущего. В этом случае полученный хеш-функцией индекс i трактуется как индекс в хеш-таблице списков, т.е. ключkeyочередной записи отображается на позициюi = h(key) таблицы. Если позиция свободна, то в нее помещается элемент с ключомkey, если же она занята, то отрабатывается алгоритм разрешения конфликтов, в результате которого такие ключи добавляются в список, начинающийся в i-й ячейке хеш-таблицы. Например, обозачив N –NULL: 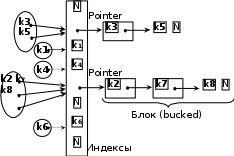 В итоге имеем таблицу массива связных списков или деревьев. Процесс заполнения (считывания) хеш-таблицы прост, но доступ к элементам требует выполнения следующих операций: вычисление индекса i; поиск в соответствующей цепочке. Для улучшения поиска при добавлении нового элемента можно использовать алгоритма вставки не в конец списка, а – с упорядочиванием, т.е. добавлять элемент в нужное место. При решении задач на практике необходимо подобрать хеш-функцию i= h(key), которая по возможности равномерно отображает значения ключа key на интервал [0, m–1], m– размер хеш-таблицы. И чаще всего, если нет информации о вероятности распределения ключей по записям, используя метод деления, берут хеш-функцию i = h(key) = key%m. При решении обратной задачи – доступ (поиск) к определенному подмножеству возможен из хеш-таблицы (хеш-структуры), которая обеспечивает по хеш-адресу (индексу) быстрый доступ к нужному элементу. ПримерыреализациисхемхешированияПримерреализацииметодапрямойадресациислинейным опробыванием. Исходными данными являются 7 записей (для простоты информационная часть состоит из целых чисел) объявленного структурного типа: struct zap { int key; // Ключ int info; // Информация } data; {59,1}, {70,3}, {96,5}, {81,7}, {13,8}, {41,2}, {79,9}; размер хеш-таблицы m = 10. Выберем хеш-функциюi= h(data) = data.key%10; т.е. остаток от деления на 10 – i�[0,9]. На основании исходных данных последовательно заполняем хеш- таблицу. Хеш-таблица (m=10)
Хеширование первых пяти ключей дает различные индексы (хеш- адреса): i = 59 % 10 = 9; i = 70 % 10 = 0; i = 96 % 10 = 6; i = 81 % 10 = 1; i = 13 % 10 = 3. Первая коллизия возникает между ключами 81 и 41 – место с индексом 1 занято. Поэтому просматриваем хеш-таблицу с целью поиска ближайшего свободного места, в данном случае – это i = 2. Следующий ключ 79 также порождает коллизию: позиция 9 уже занята. Эффективность алгоритма резко падает, т.к. для поиска свободного места понадобилось 6 проб (сравнений), свободным оказался индекс i = 4. Общее число проб – 1–9 проб на элемент. Реализацияметодацепочекдля предыдущего примера. Объявляем структурный тип для элемента однонаправленного списка: struct zap { } data; int key; // Ключ int info; // Информация zap *Next; // Указатель на следующий элемент в списке На основании исходных данных последовательно заполняем хеш- таблицу, добавляя новый элемент в конец списка, если место уже занято. Хеш-адреса i: key: info : Next : Хеш-таблица (m10) 0 1 2 3 4 5 6 7 8 9
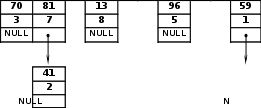 key: key: info: Next : Хеширование первых пяти ключей, как и в предыдущем случае, дает различные индексы (хеш-адреса): 9, 0, 6, 1, и 3. При возникновении коллизии новый элемент добавляется в конец списка. Поэтому элемент с ключом 41 помещается после элемента с ключом 81, а элемент с ключом 79 – после элемента с ключом 59. |
