Алгоритмизации

• Название: Алгоритмизации
• Дата: 27.09.2022
• Размер: 1.15 Mb.
• Имя файла: 12_100229_1_124427 (1).docx
• Тип: Документы; #700459
• страница: 40 из 67

Функцияпросмотра

Приведем простой пример функции вывода элементов (ключей)

дерева, использующий правила обхода 2.

void View ( Tree *t, int level ) { if ( t ) {

View ( t -> Right , level+1); // Вывод правого поддерева

for ( int i=0; i printf(" "); printf(“ %d\n”, t -> info);

View( t -> Left , level+1); // Вывод левого поддерева

}

}

Обращение к функции Viewбудет иметь вид View(Root, 0);

Функция Viewрекурсивная, вторым ее параметром является

переменная, определяющая, на каком уровне (level) находится узел. Корень находится на уровне «0». Значения узлов выводятся по горизонтали так, что корень находится слева. Перед значением узла для имитации структуры дерева выводится количество пробелов, пропорциональное уровню узла.

Если закомментировать цикл печати пробелов, значения ключей будут выведены просто в столбик.

Для последовательно введенных ключей 10 (корень), 25, 20, 6, 21, 8, 1, 30, будет построено дерево, вывод которого на экран с помощью функции View будет иметь следующий вид: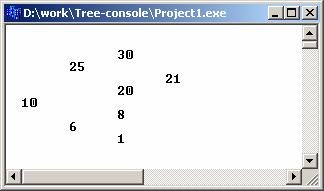

8. Освобождениепамяти

Функция освобождения памяти, занятой элементами дерева, может быть реализована аналогично рекурсивной функции View

void Del_All(Tree *t) { if ( t != NULL) {

Del_All ( t -> Left); Del_All ( t -> Right); free(t);

}

}

6. Построениеобратнойпольскойзаписи

Сложные вычислительные задачи обычно требуют больших объемов вычислений, поэтому к разработчикам языков программирования было предъявлено требование: максимально приблизить форму записи математических выражений в коде программы к естественному языку математики.

Одну из первых областей системного программирования составили исследования способов трансляции математических выражений.

В результате наибольшее распространение получил метод трансляции при помощи обратной польской записи, которую предложил польский математик Я. Лукашевич.

Рассмотрим алгоритмы получения обратной польской записи с использованием структур в виде дерева и стека.

1. Алгоритм,использующийдерево

Данный алгоритм основан на представлении математического выражения в виде дерева и использовании третьего способа его обхода (см. п. 15.5.6). Напомним его на примере арифметического выражения (A+B)*(C+D)–E.

Представим это выражение в виде дерева, в котором узлам соответствуют операции, а листьям – операнды. Построение начинается с корня, в качестве которого выбирается последняя выполняемая операция. Левой ветви соответствует левый операнд операции, а правой ветви – правый. Дерево выражения имеет вид: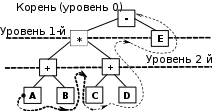




Совершим обход дерева, под которым понимается формирование строки из символов узлов и ветвей дерева. Обход будем совершать от самой левой ветви вправо и узел переписывать в выходную строку только после рассмотрения всех его ветвей. Обход совершаем строго по уровням:

1. 
   уровень 2: АВ+CD+
   
2. 
   поднялись на уровень 1: *Е
   
3. 
   и, наконец, корень: –
   

В результате такого обхода получили обратную польскую запись:

AB+CD+*E– (15.1)