кейс задача гидрогаз. КЗ 3 Шешера 018 Вариант 0 (1). Амурский государственный университет (фгбоу во АмГУ)
 Скачать 5.34 Mb. Скачать 5.34 Mb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования АМУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ (ФГБОУ ВО «АмГУ») Факультет инженерно-физический Кафедра физики Направление подготовки/специальность: 18.03.01 - «Химическая технология» кейс-задачА №3 по дисциплине «Гидрогазодинамика» номер варианта 0 Выполнила  (подпись, дата) студентка группы 018-об _________________________ В.А. Шешера Проверил  (подпись, дата) доцент, канд. физ.-мат. наук _________________________И.В. Верхотурова Благовещенск 2020 «Гизодинамический расчет сопла Лаваля» Исходные данные: Имеется сопло Лаваля (рисунок 1), имеющее конфузорную и диффузорную части с заданными углами раствора дозвуковой и сверхзвуковой частей. Заданы входные параметры газ и тип газа. 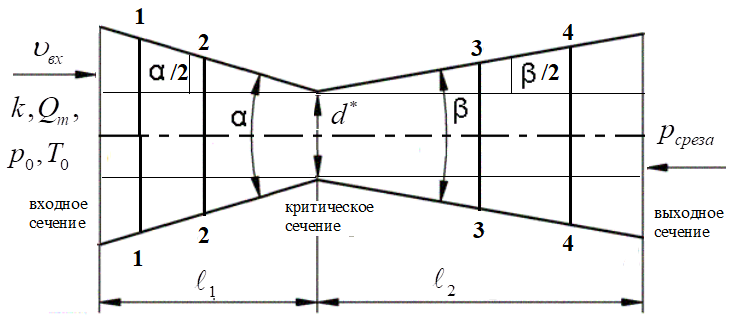 Рисунок 1 – Сопло Лаваля Таблица 1. Данные для решения задачи.
Определить: Необходимо провести газодинамический расчёт сопла Лаваля, обеспечивающего на расчётном режиме заданный расход газа. Для этого нужно провести расчёт параметров газа во входном, в критическом, в выходном и в дополнительных сечениях (1,2,3,4), определить профиль сопла и обобщить полученные результаты. Таблица 2. Физические характеристики газов.
Решение 1. Расчёт параметров газа в критическом сечении. 1.1 Рассчитаем универсальную газовую постоянную R для газа по формуле: 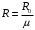 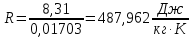 Молярную массу найдём в таблице 2. 1.2 Из уравнения Менделеева - Клайперона найдем плотность газа при полной остановке: 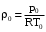 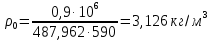 P0=0,9∙106 Па – давление торможения T0=590 К – температура торможения 1.3 Определим скорость звука в покоящемся газе а0 и скорость звука в критическом сечении, а*: Находим скорость звука при полной остановке газа: 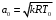 , где k – показатель адиабаты газа. , где k – показатель адиабаты газа.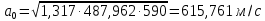 Определим скорость звука в критическом сечении: 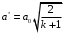 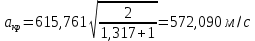 Показатель адиабаты найдём в таблице 2. 1.4 Задаваясь условием, что в критическом сечении число Маха М* = 1 и коэффициент скорости 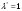 , находим скорость газового потока в критическом сечении υ*, а именно , находим скорость газового потока в критическом сечении υ*, а именно 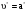 = =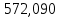 м/с. м/с.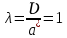 Откуда можно определить скорость газового потока в критическом сечении. Исходя из газодинамических функций параметры газа и канала в критическом сечении будут определяться по формулам: 1.5 Найдем в критическом сечении: - температуру газа 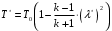 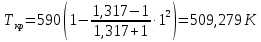 - давление газа 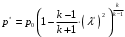 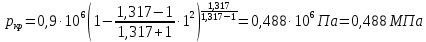 - плотность газа 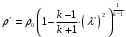 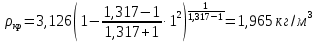 - площадь критического сечения 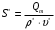 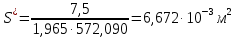 - диаметр критического сечения 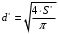 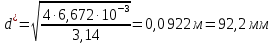 2. Расчёт параметров газа во входном сечении. 2.1 Найдем коэффициент скорости во входном сечении. 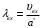 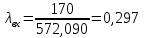 2.2. Найдем во входном сечении: - температуру газа  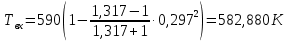 - давление газа  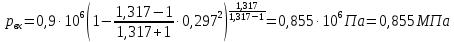 - плотность газа  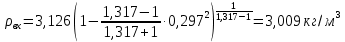 -скорость звука 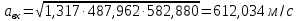 - число Маха  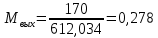 - площадь входного сечения  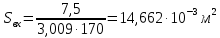 - диаметр входного сечения  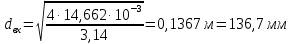 3. Расчёт параметров газа в выходном сечении. 3.1 Задаваясь условием, что давление газа в выходном сечении pвых равно давлению на срезе сопла pвых=pсреза=0,004 МПа, провести расчёт коэффициента скорости в выходном сечении 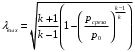 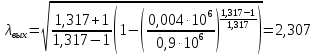 3.2 Найдем в выходном сечении - температуру газа 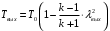 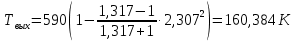 - давление газа 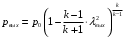 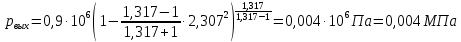 - плотность газа 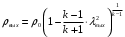 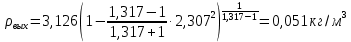 -скорость звука 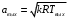 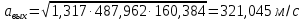 - значение скорости газа на выходе 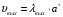 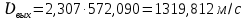 - число Маха 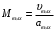 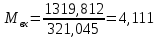 - площадь выходящего сечения 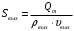 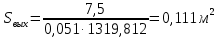 - диаметр критического сечения 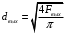 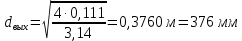 4. Геометрический профиль сопла. 4.1. Полученные значения диаметров в критическом, входном и выходном сечениях и заданные значения растворов углов сужающейся и расширяющейся частей сопла позволяют определить длины дозвуковой и сверхзвуковой частей сопла, необходимые для построения геометрического профиля сопла. Длина суживающейся (дозвуковой) части сопла определим по формуле: 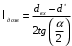 , ,где α – угол сужающейся части сопла. 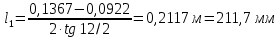 Длина расширяющейся (сверхзвуковой) части сопла определим по формуле: 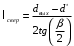 , ,где β – угол расширяющейся части сопла. 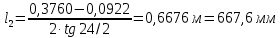 Общая длина сопла: 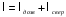 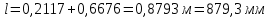 5. Расчёт дополнительных сечений. 5.1 Задаваясь условием для скорости газа в сечениях 1 и 2 υвх<υ1 < υ2 <υ* (170<υ1 < υ2 <572,090 ) проведем расчет основных параметров газа и канала в дополнительных сечениях. В сечении 1 - υ1= 400 м/с. Расчёт проводим аналогично пункту 2: Найдем коэффициент скорости в сечении. 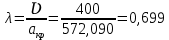 Найдем в сечении: - температуру газа 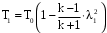 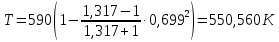 - давление газа 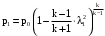 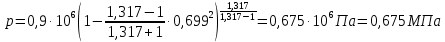 - плотность газа 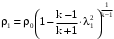 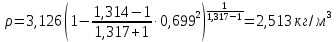 -скорость звука 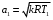 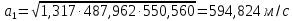 - число Маха 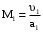 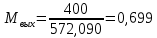 - площадь сечения 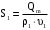 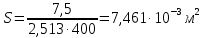 - диаметр сечения 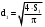 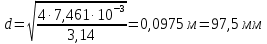 В сечении 2 – υ2= 500 м/с. Найдем коэффициент скорости в сечении. 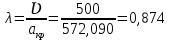 Найдем в сечении: - температуру газа 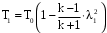 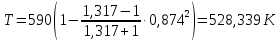 - давление газа 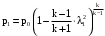 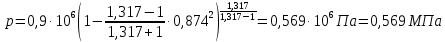 - плотность газа 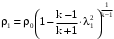 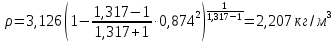 -скорость звука 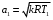 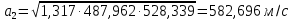 - число Маха 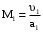 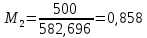 - площадь сечения 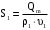 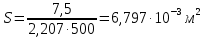 - диаметр сечения 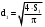 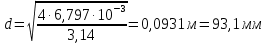 5.2 Определим расстояния между сечениями 1 и 2 и критическим сечением. 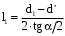 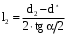 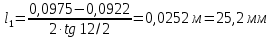 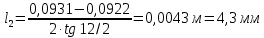 5.3 Задаваясь условием для скорости газа в сечениях 3 и 4 υ* <υ3 < υ4 <υвых (572,090<υ3 < υ4 <1319,812) проведем расчет основных параметров газа и канала в дополнительных сечениях. В сечении 3 – υ3= 1250 м/с. Найдем коэффициент скорости в сечении. 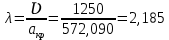 Найдем в сечении: - температуру газа 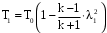 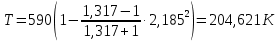 - давление газа 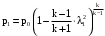 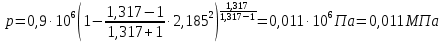 - плотность газа 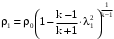 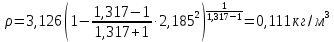 -скорость звука 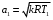 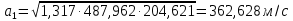 - число Маха 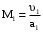 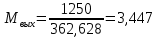 - площадь сечения 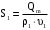 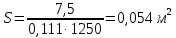 - диаметр сечения 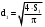 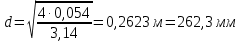 В сечении 4 – υ4= 1300 м/с. Найдем коэффициент скорости в сечении. 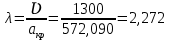 Найдем в сечении: - температуру газа 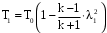 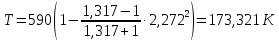 - давление газа 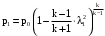 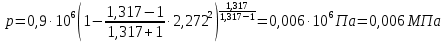 - плотность газа 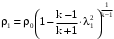 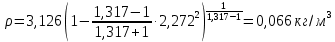 -скорость звука 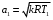 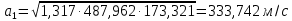 - число Маха 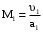 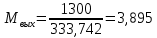 - площадь сечения 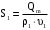 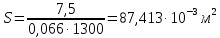 - диаметр сечения 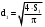 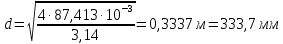 5.4 Определим расстояния между сечениями 3 и 4 и критическим сечением. 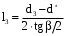 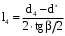 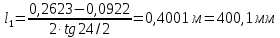 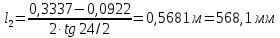 6. Результаты расчетов и выводы. Результаты расчетов представлены в таблице 3. Таблица 3.
Вывод: в ходе работы был проведён газодинамический расчёт сопла Лаваля, обеспечивающего на расчётном режиме расход газа – NH3 равный 7,5 кг/с. Для этого был произведён расчёт параметров газа во входном, в критическом, в выходном и в дополнительных сечениях (1,2,3,4). Произведя расчеты и проанализировав график зависимости параметров по длине сопла можно сделать вывод о том, что по мере движения газа по соплу: На входном сечении сохраняется максимальное давление 0,855 МПа при скорости потока 170 м/с, в выходном сечении мы имеем наименьшее давление 0,004 МПа, а скорость потока при этом возросла до 1319,812 м/с при том что площадь поперечного сечения на выходе - максимальная. Так же начальная температура уменьшилась приблизительно в 3,5 раза с 582,880 К до 160,384 К. Плотность уменьшается с 3,009 кг/м3 до 0,051 кг/м3. Скорость звука уменьшается с 612,034 м/с до 321,045 м/с. Внутренняя энергия преобразуется в кинетическую энергию направленного движения. Между числом Маха и скоростью звука в сечениях существует обратная зависимость: при уменьшении скорости звука число Маха возрастает. Давление на срезе сопла меньше давления окружающей среды (рср=0,004 МПа <ро=0,9 МПа), также в выходном сечение наблюдается повышение скорости, следовательно, наблюдается режим перерасширения. На графике это можно проследить по удлинению сверхзвуковой части сопла Лаваля по сравнению с дозвуковой. П  риложение 1. риложение 1. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
