Методика расчета. методика. Задача Подобрать площадь сечения ступенчатого бруса
 Скачать 1.14 Mb. Скачать 1.14 Mb.
|
|
Лекция для группы АДб-20Z1. Расчет на прочность и жесткость при растяжении-сжатии Задача: Подобрать площадь сечения ступенчатого бруса 1. По условию прочности определить площадь поперечного сечения согласно предложенной схемы; 2. По условию жесткости проверить полученное сечение. Из двух расчетов оставить наибольшую площадь. Исходные данные:  кН; кН;  м; м; 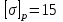 МПа; МПа;  МПа; МПа; 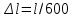 м; м; 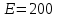 ГПа. ГПа. Рис.1. Расчетная схема ступенчатого бруса: эпюры сил; напряжений; деформаций Материал бруса – анизотропный, имеющий различные механические характеристики, выраженные в двух значениях напряжений: при растяжении и сжатии. Поэтому расчеты следует производить по двум условиям прочности (при растяжении и при сжатии). Алгоритм расчета 1. Условие прочности при данном виде загружения имеет вид  , (1) , (1)где 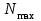 – значение максимальной продольной (нормальной) силы в опасном сечении, кН; – значение максимальной продольной (нормальной) силы в опасном сечении, кН;  – площадь поперечного сечения бруса, м2 ; – площадь поперечного сечения бруса, м2 ;  – допускаемое значение нормального напряжения материала. – допускаемое значение нормального напряжения материала.2. По условию прочности необходимо построить эпюру продольных сил и, для каждого вида нагружений, определить максимальные значения. 2.1. За точку отсчета примем свободный конец (консоль). 2.2. На каждом участке выберем произвольные сечения с координатами привязки от начала каждого участка. 2.3. Определим границы изменения отсеченных частей. 2.4. Запишем уравнения равновесия внутренних продольных усилий на отсеченных частях с учетом знаков. Первый участок.  ; ;  кН. кН.Второй участок.  ; ;  – отсеченная часть второго сечения; – отсеченная часть второго сечения;  кН. кН.Третий участок.  ; ;  – отсеченная часть третьего сечения; – отсеченная часть третьего сечения;  кН. кН.Эпюра продольных сил представлена на рис.1 под схемой. Для определения опасных сечений по напряжениям, строим эпюру напряжений, используя зависимость 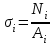 (2) (2)Здесь силы и площади на каждом участке.  МПа; МПа; МПа; МПа; МПа. МПа.Эпюра напряжений представлена на рис.1 под эпюрой сил. Анализ эпюры напряжений показывает, что первые два участка определяют область растяжения (+), третий – область сжатия (-). Производим два расчета на прочность. Первый – растяжение. Условие прочности при растяжении  (3) (3)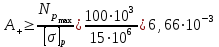 м2 . м2 .Второй – сжатие. Условие прочности при сжатии  (4) (4) м2 . м2 .Вывод: Оставляем площадь большую, полученную из условия прочности при растяжении –  м2 . м2 .Проверка принятого сечения по условию жесткости. Рассмотрим закон Гука при растяжении-сжатии  . .Нормальное напряжение – прямо пропорционально относительной деформации (в области упругости).  – коэффициент пропорциональности, модуль упругости первого рода, модуль Юнга. – коэффициент пропорциональности, модуль упругости первого рода, модуль Юнга.Относительная деформация – отношение абсолютной деформации к первоначальной длине тела (стержня)  и и 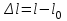 , ,где  – длина стержня после загружения внешней силой. – длина стержня после загружения внешней силой.Раскроем левую и правую части закона Гука  ; отсюда ; отсюда  . (5) . (5)Знаменатель представляет нормальную жесткость стержня, включающую механическую характеристику материала – модуль упругости и геометрическую характеристику – площадь сечения. Условие жесткости при растяжении-сжатии по условию задачи  (6) (6)3.1. Отсчет производим от защемления, принимая нулевую деформацию в защемлении. Координаты отсеченных частей на каждом участке примут вид. Третий участок   м; м;Второй отдельный участок   м; м;Первый отдельный участок   м. м.На рис. 1 под эпюрой напряжений изображена эпюра абсолютных несовместных деформаций – раздельных на каждом участке. Для создания полной картины совместных деформаций необходимо в начало третьего участка вставить эпюру второго и в начало совместного третьего-второго эпюру первого. Таким образом – алгебраическая сумма ординат эпюр от третьего к первого и определит эпюру совместных абсолютных деформаций. На рис.1 последняя эпюра и есть искомая. Тогда, наибольшая абсолютная деформация в данной задаче – сечение свободного конца  м. м.3.2. По условию жесткости, определим площадь опасного сечения 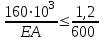 или или  м2 . м2 .Приведем к единой степени  м2 . м2 .Сравнивая две площади, принимаем решение. Оставить площадь  м2 как наибольшую, отвечающую условиям прочности и жесткости. м2 как наибольшую, отвечающую условиям прочности и жесткости.В задачах принять: модуль упругости  МПа; МПа;абсолютную деформацию 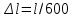 Исходные данные к задачам
Расчетные схемы  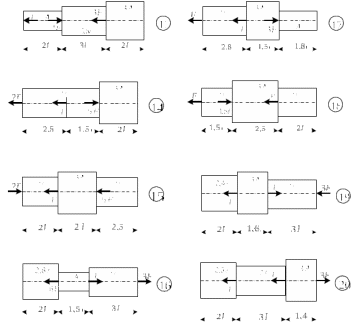 |


