РАСЧЁТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ По дисциплине: «Сопротивление материалов» Тема: «Простое сопротивление» СФУ. Расчетно-графические задачи, Петров Е.О. Простое сопротивление
 Скачать 309.82 Kb. Скачать 309.82 Kb.
|
|
Федеральное государственное автономное образовательное учреждение высшего образования «СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» Политехнический институт Кафедра «Прикладная механика» РАСЧЁТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ По дисциплине: «Сопротивление материалов» Тема: «Простое сопротивление» Вариант №19
Красноярск 2021 СОДЕРЖАНИЕЗадача №1: Подбор размеров сечения стержней стержневой системы Рисунок 1 — Схема приложения усилий
Решение: Принимаем все стержни растянутыми, направляем усилия в стержнях в сторону отброшенных связей (рис. Рисунок 1). Составим уравнения равновесия для определения усилий N1, N2, N3:  (1.1) (1.1) (Стержень растянут) (1.2) (Стержень растянут) (1.2)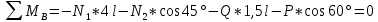 (1.3) (1.3) (Стержень сжат) (1.4) (Стержень сжат) (1.4) (1.5) (1.5) (Стержень сжат) (1.6) (Стержень сжат) (1.6)Проверка:  (1.7) (1.7)Определим площади поперечного сечения стержней, запишем условия прочности для растянутых и сжатых стержней:  (1.8) (1.8)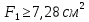 (Минимальная площадь первого стержня) (1.9) (Минимальная площадь первого стержня) (1.9)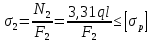 (1.10) (1.10) (Минимальная площадь второго стрежня) (1.11) (Минимальная площадь второго стрежня) (1.11) (1.12) (1.12)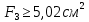 (Минимальная площадь третьего стержня) (1.13) (Минимальная площадь третьего стержня) (1.13)Назначим размеры стержней: 1-ый стержень круглый, тогда  (1.14) (1.14)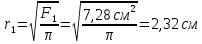 (1.15) (1.15)2-ой стержень круглый, тогда 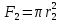 (1.16) (1.16) (1.17) (1.17)3-ий стержень квадратный, тогда 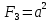 (1.18) (1.18)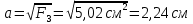 (1.19) (1.19)Вывод: В ходе решения задачи были определены: Продольные усилия в стержнях N1 = –2,23ql , N2 = 3,31ql, N3 = –1,54ql Минимально возможные площади поперечных сечений стержней: F1 ≥ 7,28 см2, F2 ≥ 3,24 см2, F3 ≥ 5,02 см2. Размеры стержней: r1 = 2,32 см, r2 = 1,03 см, a = 2,24 см. Задача №2: Проектный расчет ступенчатого бруса Рисунок 2 — Схема ступенчатого бруса и эпюры продольных сил и перемещений
Решение: Составим уравнение равновесия:  (2.1) (2.1)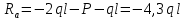 (2.2) (2.2)Для определения продольных сил используем метод сечений, составим выражения для определения N по участкам бруса: 1 участок:   (2.3) (2.3) , (2.4) , (2.4)При 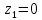 продольная сила продольная сила  , если , если 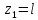 , то , то  2 участок: 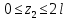 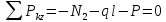 (2.5) (2.5)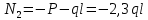 (2.6) (2.6)3 участок: 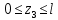 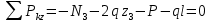 (2.7) (2.7)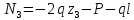 , (2.8) , (2.8)При 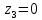 продольная сила продольная сила  , если , если  , то , то  Составим выражение для нормальных напряжений по участкам бруса:  , (2.9) , (2.9)При  нормальное напряжение нормальное напряжение 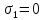 , если , если  , то , то 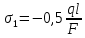  (2.10) (2.10) , (2.11) , (2.11)При  нормальное напряжение нормальное напряжение 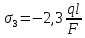 , если , если  , то , то 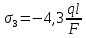 Подберем размеры сечений: Запишем условие прочности для наиболее опасного сечения: 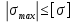 , где , где  , тогда (2.12) , тогда (2.12)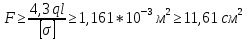 (2.13) (2.13)Назначим площади всех участков: 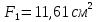 , , 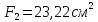 Определим абсолютные деформации участков бруса: 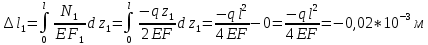 (2.14) (2.14)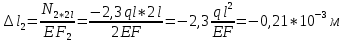 (2.15) (2.15)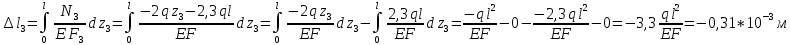 (2.16) (2.16)Определим продольные перемещения характерных участков бруса: 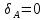 (2.17) (2.17)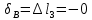 , , (2.18) (2.18) (2.19) (2.19)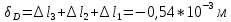 (2.20) (2.20)Выполним проверку на жесткость: 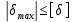 , где , где  , (2.21) , (2.21)Условие жесткости не выполняется, поэтому необходимо увеличить величины поперечных сечений бруса: 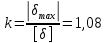 (2.22) (2.22)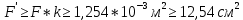 (2.23) (2.23)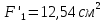 , , 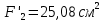 Вывод: В ходе решения задачи были построены эпюры продольных сил и перемещений, определена площадь поперечного сечения, удовлетворяющая условиям прочности и жесткости 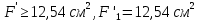 , , 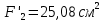 Задача №3: Проектный расчет ступенчатого статически неопределимого бруса Рисунок 3 — Схема ступенчатого бруса и эпюры продольных сил и перемещений
Решение: Составим уравнения равновесия и перемещений: 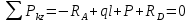 (3.1) (3.1)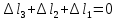 (3.2) (3.2)Для определения продольных сил используем метод сечений, составим выражения для определения N по участкам бруса: 1 участок:  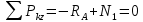 (3.3) (3.3) (3.4) (3.4) (3.5) (3.5)2 участок: 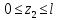  (3.6) (3.6)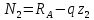 , (3.7) , (3.7)При  продольная сила продольная сила 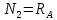 , если , если 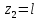 , то , то 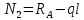 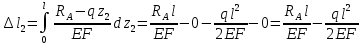 (3.8) (3.8)3 участок: 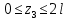  (3.9) (3.9)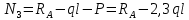 (3.10) (3.10)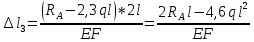 (3.11) (3.11)Подставим абсолютные деформации в формулу (3.2): 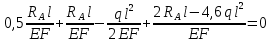 (3.12) (3.12)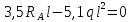 (3.13) (3.13)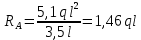 (3.14) (3.14)Из уравнения равновесия (3.1): 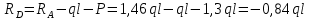 (3.15) (3.15)Зная RA, найдем продольные силы:  (3.16) (3.16)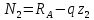 , (3.17) , (3.17)При  продольная сила продольная сила  , если , если 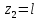 , то , то  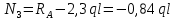 (3.18) (3.18)Составим выражение для нормальных напряжений по участкам бруса: 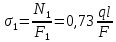 (3.19) (3.19)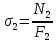 , (3.20) , (3.20)При  нормальное напряжение нормальное напряжение 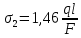 , если , если 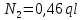 , то , то 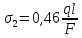  (3.21) (3.21)Подберем размеры сечений: Запишем условие прочности для наиболее опасного сечения: 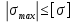 , где , где 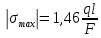 , тогда (3.22) , тогда (3.22) (3.23) (3.23)Назначим площади всех участков: 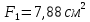 , , 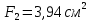 Определим абсолютные деформации участков бруса: 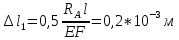 (3.24) (3.24) (3.25) (3.25)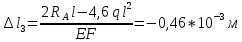 (3.26) (3.26)Определим продольные перемещения характерных участков бруса: 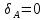 (3.27) (3.27)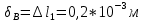 (3.28) (3.28) (3.29) (3.29) (3.30) (3.30)Выполним проверку на жесткость: 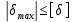 , где , где  , (3.31) , (3.31)Условие жесткости выполняется. Вывод: В ходе решения задачи были построены эпюры продольных сил и перемещений, определены величины реактивных сил, возникающих в жестких заделках:  , , 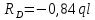 , а также площадь поперечного сечения, удовлетворяющая условиям прочности и жесткости , а также площадь поперечного сечения, удовлетворяющая условиям прочности и жесткости 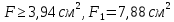 , , 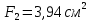 Задача №4: Вычисление геометрических характеристик несимметричных сечений из простых фигур Рисунок 4 — Схема несимметричного сечения
Решение: Выберем вспомогательные оси YOX (рис. Рисунок 4), определим координаты центра тяжести составного сечения, состоящего из трех фигур: прямоугольника и двух одинаковых кругов: Для прямоугольника: Центр тяжести в точке C1(x1;y1) = С1(0;0) относительно YOX Площадь: b = 9a, h = 6a  (4.1) (4.1)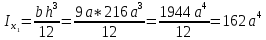 (4.2) (4.2) (4.3) (4.3)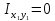 (4.4) (4.4)Для кругов: Центры тяжести в точке C2(x2;y2) = С2(–2,5a;–a) C3(x3;y3) = С3(2,5a;a) относительно YOX Площади: d = 2a  (4.5) (4.5) (4.6) (4.6) (4.7) (4.7)Определим координаты общего центра тяжести фигуры: 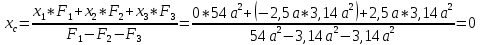 (4.8) (4.8) (4.9) (4.9)Cc(xc;yc) = Сc(0;0) Определим осевые и центробежный моменты инерции всего сечения: 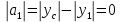 (4.10) (4.10) (4.11) (4.11)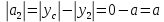 (4.12) (4.12)Будет отрицательным  (4.13) (4.13)Будет отрицательным 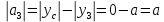 (4.14) (4.14)Будет положительным  (4.15) (4.15)Будет положительным  (4.16) (4.16) (4.17) (4.17)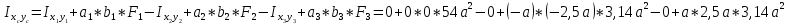 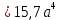 (4.18) (4.18)Вывод: В ходе решения задачи мы определили центр тяжести сечения 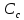 ( ( ) , мы определили осевые и центробежные моменты инерции сечения ) , мы определили осевые и центробежные моменты инерции сечения  , ,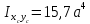 Задача №5: Вычисление геометрических характеристик несимметричных сечений из прокатных профилей |
