ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 2 по Механике 1.3 Вариант 66, 37 ТЕМА: Метод сечений в сопротивлении материалов.. Метод сечений в сопротивлении материалов
 Скачать 1.13 Mb. Скачать 1.13 Mb.
|
|
Национальный исследовательский Томский политехнический университет  ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 2 по Механике 1.3 Вариант 6/6, 3/7 ТЕМА: Метод сечений в сопротивлении материалов. Выполнил: _______________________________ (дата, подпись) Проверил: проф. Томилин А.К. _______________________________ (оценка, дата, подпись) Томск, 2022 Задача 1. Сжатие-растяжение ступенчатого стержня. Условие: Стальной стержень находится под действием продольных сил. Влиянием собственного веса стержня пренебречь. Дано: А1= 300 мм2, А2= 150 мм2, А3= 200 мм2, F1= 30 кН, F2= 10 кН, F3= 45 кН, l= 1 м, E= 2*105 МПа, P= 0 Н, G=0,8*104 кН/м2 Построить: эпюры внутренних продольных сил, нормальных напряжений и перемещений. 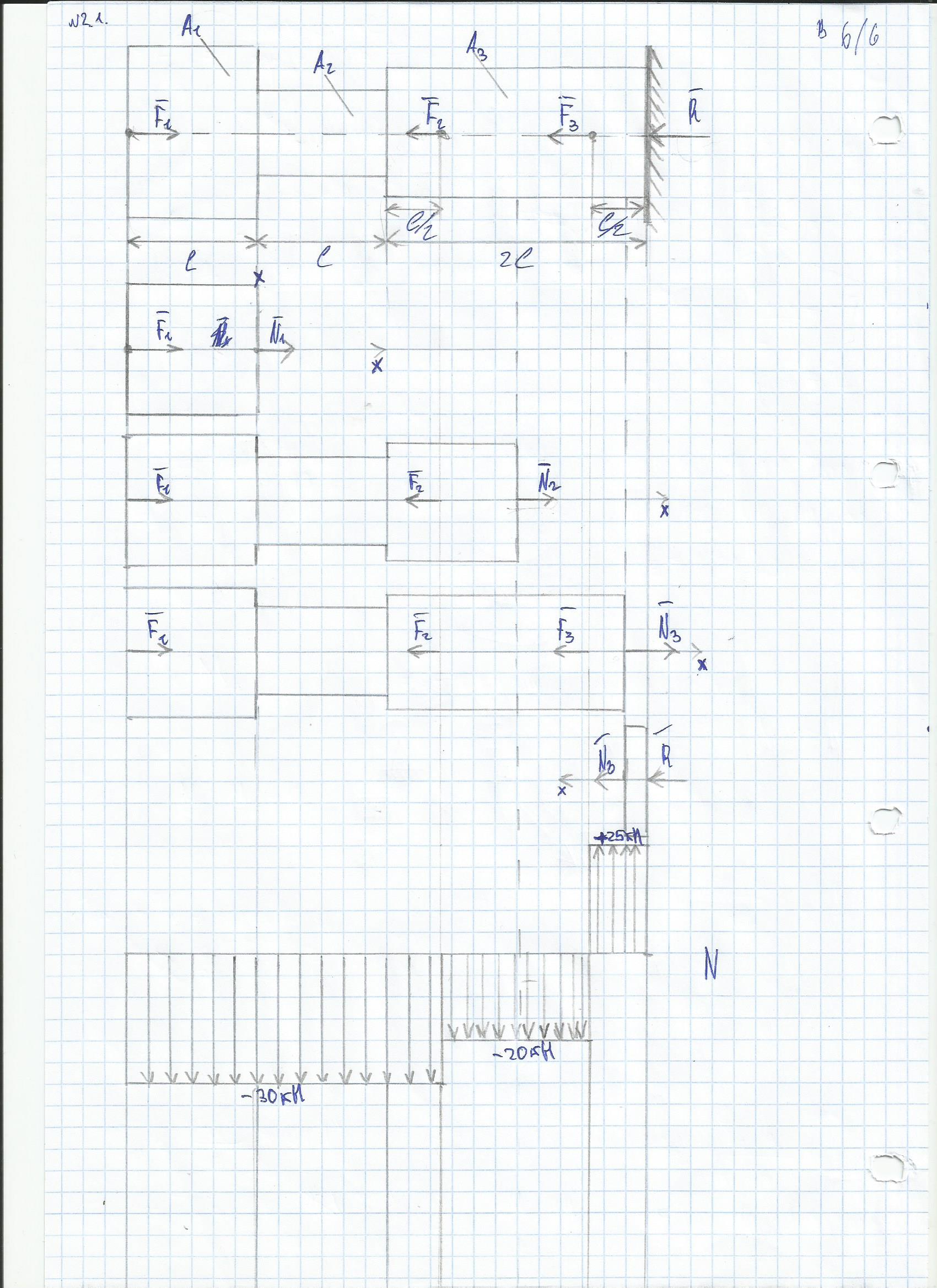 Рис. 1 Твердое тело представляет собой ступенчатый стальной стержень, закрепленный в стене. Поэтому возникает сила R. Решение: Ⅰ) Для начала определим реакцию заделки: - R -F3 – F2 + F1 = 0; Выразим и найдем из этого уравнения R: R = F1 - F2 – F3; R = -25кН Выполним разрезы в любых местах между участками действия сил, но не на границах действия самих сил. Начинаем от начала стержня слева направо. Определяем реакцию заделки: 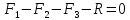 Или 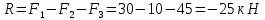 Первый участок: 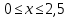 Условие равновесия первого левого участка: 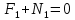 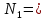 - -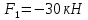 Первый участок испытывает сжатие. Второй участок:  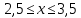 Условие равновесия второго участка: 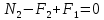 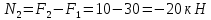 Второй участок испытывает сжатие. Третий левый участок:  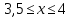 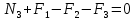 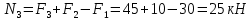 Третий левый участок испытывает растяжение. Третий правый участок:   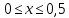 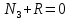 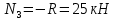 Третий правый участок испытывает растяжение. Ⅱ) Расчет нормальных напряжений. На участке 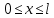 с сечением с сечением 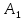 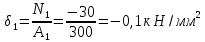 На участке 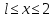 с сечением с сечением 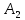 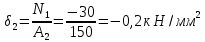 На участке 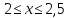 с сечением с сечением 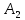 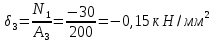 На участке 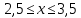 с сечением с сечением 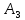 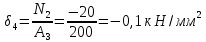 На участке 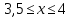 с сечением с сечением 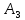 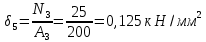 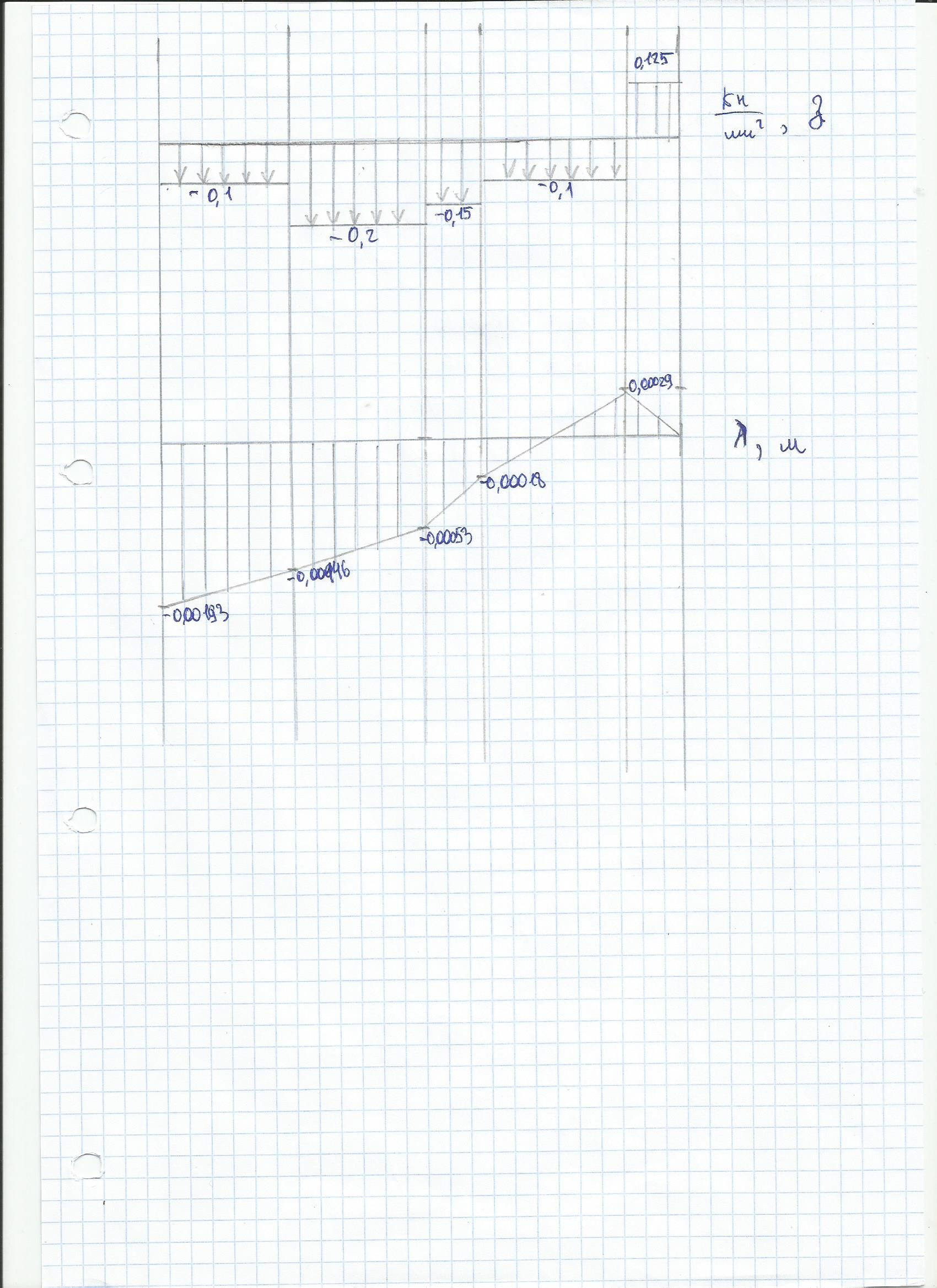 Рис.2 Ⅲ) Расчет смещений На первом справа участке: 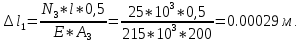 На втором справа участке 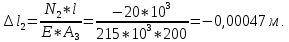 На третьем справа участке 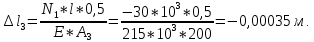 На четвертом справа участке 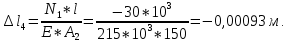 На пятом справа участке 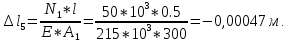 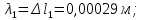 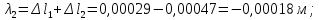 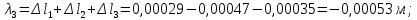 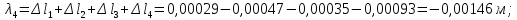 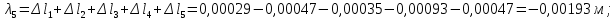 Задача 2. Кручение. Расчет вала на прочность и жесткость. Условие. К стальному валу постоянного поперечного сечения приложены четыре внешних скручивающих момента. Требуется построить эпюру крутящих моментов, определить диаметр вала при τ = 8 кН/см2 и построить эпюру углов закручивания поперечных сечений стержня. G = 0,8 * 104 кН/см2. Дано: М1 = 2,0 кН*м; М2 = 3,0 кН*м; М3 = 1,2 кН*м; М4 = 1,0 кН*м; а = 1,5 м; b = 1,5 м; с = 1,3 м; d = 1,3 м; G = 0,8 * 104 кН/см2; τ = 8 кН/см2.  Рис. 1 Тело представляет собой стальной вал постоянного поперечного сечения с закрепленным левым концом в стене. Из-за этого возникает крутящий момент МА. Решение: Определяем момент сил в заделке: 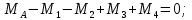 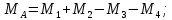 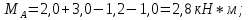 Разделив весь вал на четыре участка, применим метод сечений на каждом из них. В месте сечений возникают внутренние моменты T. Рассмотрим каждое сечение отдельно, начиная отсекать справа на лево: Сечение 1-1: T1 + M4 = 0; T1 = M4; T1 = -1,0 кН * м; Сечение 2-2: T2 + M4 + M3= 0; T2 = -M4 - M3 = -1-1,2 = -2,2 кН * м; Сечение 3-3: T3 + M4 + M3 - M2= 0; T3 = -M4 - M3 + M2 = -1,0 – 1,2 +3,0 = 0,8 кН * м; Сечение 4-4: T4 – MА = 0; T4 = MА = 2,8 кН * м; Определим диаметр вала: Условие прочности: τmax = 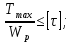 Полярный момент сопротивления: 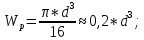 В нашем случае: Tmax = T4 = 280 кН * см; Требуемый диаметр вала: 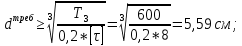 Диаметр вала равен d = 58 мм. Определяем углы закручивания: Полярный момент инерции для круглого сечения: 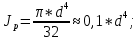 Вычисляем крутильную жесткость: G*Jp = 0,8 * 104 * 0,1*5,84 = 905319 кН * см2; . Находим углы закручивания на участках: Участок A-B: 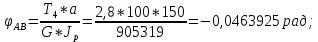 Участок B-C: 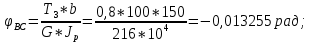 Участок C-D: 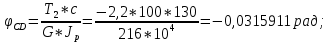 Участок D-E: 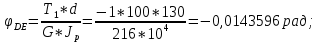 Определяем углы закручивания в точках: φB = φAB = 0,0463925 рад. φC = φB + φBC = 0,0463925 + 0,013255 = 0,0596475 рад. φD = φC + φCD = 0,0596475 - 0,0315911= 0,0280564 рад. φE = φD + φDE = 0,0280564 – 0,0143596= 0,0136968 рад. Ответ: d = 58 мм. |
