национальныйисследовательскийтомский политехнический университет

• Название: национальныйисследовательскийтомский политехнический университет
• Дата: 11.12.2022
• Размер: 0.62 Mb.
• Имя файла: MEKh_IDz_3.docx
• Тип: Документы; #838331

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«НАЦИОНАЛЬНЫЙИССЛЕДОВАТЕЛЬСКИЙТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»




«Растяжение-сжатие, кручение, изгиб»
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 3

Вариант 02303

по дисциплине:

Механика

Исполнитель:
студент группы	5А96	Акатьев Дмитрий Константинович	12.12.2020
Руководитель:		Коноваленко Игорь Сергеевич
преподаватель

Томск – 2020

1. РАСТЯЖЕНИЕ-СЖАТИЕ

Металлический ступенчатый стержень находится под действием сосредоточенных сил. Физико-механические характеристики материала стержня: Е=2·10⁵ МПа; [Δl] =3·10-4 мм; [σ]=160 МПа. Длину а, во всех вариантах принять равной 2м.

Для заданной схемы стержня требуется:

1. 
   В масштабе изобразить поперечные сечения и длины стержня.
   
2. 
   Определить реакцию опоры.
   
3. 
   Составить аналитические выражения и построить эпюры поперечных сил, продольных напряжений, изменения длины.
   

Исходные данные: схема стержня представлена на рисунке 1. Сосредоточенная сила Р₁=19 кН;

Сосредоточенная сила Р₂=20 кН;

Сосредоточенная сила Р₃=13 кН;

Площадь поперечного сечения стержня А =190 мм²;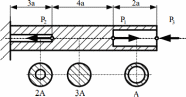




Рис. 1. Схема стрежня
Решение:

Изобразим расчётную схему стержня, соблюдая масштаб.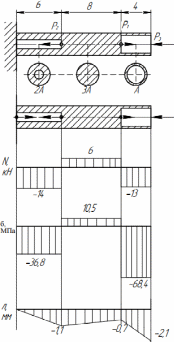


Рис. 2. – Стержень загруженный внешними продольными силами; эквивалентная схема нагружения стержня; эпюры продольных сил нормальных напряжений и перемещение свободного конца стержня.

Находим реактивную силу R из уравнения равновесия:

∑ 𝐹_𝑍 = 0;

𝑅 + 𝑃₁ − 𝑃₂ − 𝑃₃ = 0;

𝑅 = −𝑃₁ + 𝑃₂ + 𝑃₃ = −19 + 20 + 13 = 14 (кН);

*Знак «-» означает, что произвольное направление R выбрано верно.

Применяем метод сечений, оставляя левую и отбрасывая правую часть бруса. Для определения продольных сил разделим стержень на три участка.

1. 
   ыйучасток:
   

^{∑ 𝐹}𝑍 ^{= 0;}

𝑁₁ + 𝑅 = 0;

𝑁₁ = −𝑅 = −14 (кН);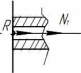

2. 
   ойучасток:
   

^{∑ 𝐹}𝑍 ^{= 0;}
𝑁₂ − 𝑃₂ + 𝑅 = 0;

𝑁₂ = −𝑅 + 𝑃₂ = −14 + 20 = 6 (кН);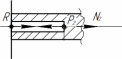

3. 
   ий участок:
   

^{∑ 𝐹}𝑍 ^{= 0;}
−𝑁₃ − 𝑃₃ = 0;

𝑁₃ = −𝑃₃ = −13 (кН);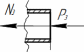



Определение нормальных напряжений.

Нормальные напряжения, действующие в сечениях каждого участка, определим из условия прочности:

𝑁₁ −14 ∙ 10³

σ₁ = _2𝐴 = _{2 ∙ 190 ∙ 10−6} = −36,8 (МПа);

𝑁₂ 6 ∙ 10³

σ₂ = _3𝐴 = _{3 ∙ 190 ∙ 10−6} = 10,5 (МПа);

σ₃ =

𝑁_{3 =}

𝐴

−13 ∙ 10³

_{190 ∙ 10−6} = −68,4 (МПа);

По полученным значениям строим эпюру нормальных напряжений.
Определение деформации стержня

При растяжении (сжатии) бруса его поперечные сечения перемещаются

в направлении сил. Перемещения являются следствием деформаций. Перемещение произвольного сечения бруса равно изменению длины участка,

заключенного между этими сечениями и заделкой.

𝐹 · 𝑧

𝜆 = 𝛥𝑙 = _{𝐸 · 𝐴} =

𝜎 · 𝑧


𝐸

Где E - модуль продольной упругости или модуль упругости I-го рода. Для стали E = (1,9…2,15)·10⁵ (МПа).

Примем E = 2·10⁵ (МПа),
^{𝜆 = ∑ 𝛥𝑙}𝑖^;
Перемещение равно алгебраической сумме перемещений всех участков стержня.

𝜆_в = 0;

−36,8 ∙ 10⁶ ∙ 6


2 ∙ 10
_{𝜆м = 𝜆в + 𝜆вм = 0 + ∆𝑙1 = 11} = −1,1 ∙ 10⁻³ (м)

10,5 ∙ 10⁶ ∙ 8

𝜆_с = 𝜆_м + 𝜆_см = ∆𝑙₁ + ∆𝑙₂ = −1,1 ∙ 10⁻³ +

2 ∙ 10

−68,4 ∙ 10⁶ ∙ 4

₁₁ = −0,7 ∙ 10⁻³ (м)

𝜆_к = 𝜆_с + 𝜆_кс = −0,7 ∙ 10⁻³ +

= −2,1 ∙ 10⁻³ (м)


11
2 ∙ 10

2. КРУЧЕНИЕ

Металлический ступенчатый вал находится под действием сосредоточенных скручивающих моментов.

Для заданной схемы вала, требуется:

1. 
   Составить аналитические выражения и построить эпюру крутящего момента.
   
2. 
   В масштабе изобразить длины и поперечные сечения вала на каждом силовом участке и построить эпюры распределения касательных напряжений.
   
3. 
   Построить эпюру абсолютных углов закручивания по длине вала.
   

Исходные данные: схема стержня представлена на рисунке

3. 
   Расстояние а=2 м;
   

внешний сосредоточенный момент М₁ =490 Нм; внешний сосредоточенный моментов М₂ =270 Нм; внешний сосредоточенный моментов М₃ = 250 Нм; внешний сосредоточенный моментов М₄ = 370 Нм; параметры поперечного сечения d=h=36 мм; соотношение параметров вала d/D=0,7;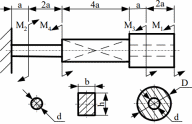


h/b=1,2;
Рис.3. Схема вала
Решение:

Изобразим расчетную схему стержня, соблюдая масштаб по длине.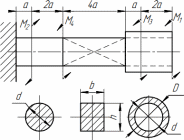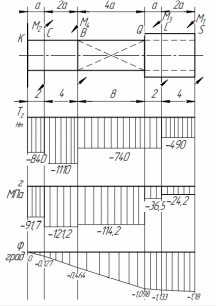






Рис. 4. – Расчетная схема вала в масштабе по длине, эпюры внутренних крутящих моментов, касательных напряжений и угла поворота свободного конца вала.

Из уравнения равновесия,находим величину и направление реактивного момента в опоре 𝑀_𝐾 .

^{∑ 𝑀}𝑖 ^{= 0;
−𝑀}𝐾 ^{+ 𝑀}2 ^{– 𝑀}4 ^−𝑀3 ^{– 𝑀}1 <sup>= 0;

𝑀</sup>𝐾 ^{= -𝑀}1 ^{- 𝑀}3 ^{+ 𝑀}2 ^{− 𝑀}4 ^{= - 370 - 250 - 490 + 270 = −840 (кНм);}

Определим геометрические размеры сечения вала:

𝐷 =
𝑏 =

𝑑

=

0,7

ℎ

=

1,2

36 · 10⁻³

0,7

36 · 10⁻³


1,2
= 51,4 · 10⁻³ (м);
= 30 · 10⁻³ (м);

Построим эпюру внутренних крутящих моментов, для этого разобьем вал на силовые участки:

𝑇_𝑧1 = 𝑀_𝐾 = −840 (Нм);

𝑇_𝑧2 = 𝑀_𝐾 − 𝑀₂ = −840 − 270 = −1440 (Нм);

𝑇_𝑧3 = 𝑀_𝐾 − 𝑀₂+𝑀₄ = −840 − 270 + 370 = −740 (Нм);

𝑇_𝑧4= 𝑀_𝐾 − 𝑀₂+𝑀₄ + 𝑀₃ = −840 − 270 + 370 + 250 = −490 (Нм);

Напряжения кручения находятся по формуле:

𝑇_𝑧

_𝜏𝑧 =

;

𝑊_𝜌

где 𝑊_𝜌 - полярный момент сопротивления или момент сопротивления сечения кручению.

Полярный момент сопротивления для прямоугольного сечения:

𝑏 · ℎ²

𝑊^П = ;

𝜌 ₆

Полярный момент сопротивления для кольцевого сечения:

_⊚ 𝜋 · 𝐷³

𝑑

)⁴| ;

𝑊_𝜌 =

|1 − (


16
𝐷

Полярный момент сопротивления для сплошного круга:

_◯ 𝜋 · 𝑑³

𝑊_𝜌 = ₁₆ ^;

_{τ =} ^𝑇𝑧1

^{1 𝑊}𝑝1

−840 ∙ 16

⁼ 3,14 ∙ (36 ∙ 10⁻³)³

= −91,7 (Мпа)

_{τ =} ^𝑇𝑧2

^{2 𝑊}𝑝1

_{τ =} ^𝑇3𝑧

−1110 ∙ 16

⁼ 3,14 ∙ (36 ∙ 10⁻³)³

₌ −740 ∙ 6
= −121,2 (Мпа)
= −114,2 (Мпа)

^{3 𝑊}𝑝2

_{τ =} ^𝑇𝑧3 ^{4 𝑊}𝑝3


30 ∙ 10⁻³ ∙ (36 ∙ 10⁻³)²

−740 ∙ 16

⁼ 3,14 ∙ (51,4 ∙ 10⁻³)³ ∙ (1 − (0,7)⁴)

= −36,5 (Мпа)

_{τ =} ^𝑇𝑧4

^{5 𝑊}𝑝3

−490 ∙ 16

⁼ 3,14 ∙ (51,4 ∙ 10⁻³)³ ∙ (1 − (0,7)⁴)
= −24,2 (Мпа)

Определим повороты сечения для каждой части стержня, где крутящие моменты и жесткости постоянны по длине:

_{𝜑 =} 𝑇_𝑧 · 𝑙 _;

𝐽
1

𝜌

• 
  𝐺
  

эта формула действительна только для части стержня постоянного сечения по длине l.

где G=8·10⁴ МПа – модули упругости II – рода;

𝐽_𝜌 - полярный момент инерции поперечного сечения стержня;

Полярный момент инерции для прямоугольного сечения:

𝜌
𝐽^П =

𝑏 · ℎ³ 12

30 · 10⁻¹² · 36³

=

12
= 116640 · 10⁻¹² (м⁴);

Полярный момент сопротивления для кольцевого сечения:

_⊚ 𝜋 · 𝐷<sup>4

𝑑</sup> 3,14 · 51,4⁴ · 10⁻¹²

30 · 10⁻³

𝐽_𝜌 =

|1 − (


32
𝐷

)⁴| =

|1 − (_{51,4 · 10−3} )⁴| =

32
= 520461,5 · 10⁻¹² (м⁴);
Полярный момент сопротивления для сплошного круга:

𝐽^◯=

𝜋 ·𝑑⁴

3,14 · 36⁴ · 10⁻¹²

=
= 164812 · 10⁻¹² (м⁴);

^𝜌 32 32

Поворот сечения C относительно K:

φ

𝐶/𝐾

₌ 𝑇_𝑍1 ∙ 2

𝐺 ∙ 𝐽_𝑝1

−840 ∙ 2

⁼ 8 ∙ 10¹⁰ ∙ 164812 ∙ 10⁻¹²
= −0,127;

Поворот сечения B относительно C:

φ

𝐵/𝐶

₌ 𝑇_𝑍2 ∙ 4

𝐺 ∙ 𝐽_𝑝1

−1110 ∙ 4

⁼ 8 ∙ 10¹⁰ ∙ 164812 ∙ 10⁻¹²
= −0,337;

Поворот сечения Q относительно B:

φ

𝑄/𝐵

₌ 𝑇_𝑍3 ∙ 8

𝐺 ∙ 𝐽_𝑝2

−740 ∙ 8

⁼ 8 ∙ 10¹⁰ ∙ 116640 ∙ 10⁻¹²
= −0,634;

Поворот сечения L относительно Q:

φ

𝐿/𝑄

₌ 𝑇_𝑍3 ∙ 2

𝐺 ∙ 𝐽_𝑝3

−740 ∙ 2

⁼ 8 ∙ 10¹⁰ ∙ 520461,5 ∙ 10⁻¹²
= −0,035;

Поворот концевого сечения S относительно L:

φ

𝑆/𝐿

₌ 𝑇_𝑍4 ∙ 4

𝐺 ∙ 𝐽_𝑝3

−490 ∙ 4

⁼ 8 ∙ 10¹⁰ ∙ 520461,5 ∙ 10⁻¹²
= −0,047;

По вычисленным значениям углов определяются повороты всех сечений относительно неподвижного сечения K.

^𝜑𝑆⁄𝐾 ^{= 𝜑}𝐶⁄𝐾 ^{+ 𝜑}𝐵⁄𝐶 ^{+ 𝜑}𝑄⁄𝐵 ^{+ 𝜑}𝐿⁄𝑄 ^{+ 𝜑}𝑆⁄𝐿 = −0,127 − 0,337 − 0,634 − 0,035 −

0,047 = −1,18;

3. ИЗГИБ

Металлическая балка находится под действием сосредоточенных внешних сил, распределенной нагрузки, сосредоточенного изгибающего момента. Величины нагрузок приведены в табл. 3.3. Длину а, во всех вариантах принять равной 2м.

Для заданной схемы балки, требуется:

1. 
   Составить аналитические выражения и определить реакции в опоре.
   
2. 
   Построить эпюры поперечных сил и изгибающих моментов.
   
3. 
   Подобрать размеры поперечного сечения: двутавровое; круглое – диаметром d.
   

В масштабе изобразить поперечные сечения балки.

Исходные данные: схема стержня представлена на рисунке 5. Расстояние а=2 м;

Изгибающий момент М=14 кНм; Сосредоточенная сила P₁=35 кН; Сосредоточенная сила P₂=30 кН; Распределенная нагрузка q=20 кН/м;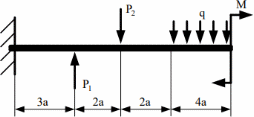




Решение:

^{Построить эпюры поперечных сил Q и изгибающих моментов M}и^.

Изобразим стержень, соблюдая масштаб его участков по длине.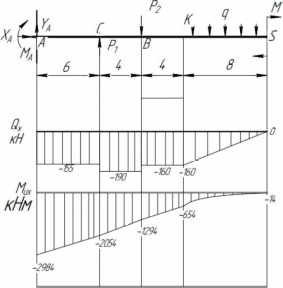


Определим реакции в опоре А:
^{∑ 𝑋 = 𝑋}𝐴 ^{= 0;
∑ 𝑚}𝐴 ^{= −𝑀}𝐴 ^{+ 𝑃}1^{∙ 6 − 𝑞 ∙ 8 ∙ (6 + 4+4+4) − 𝑃}2^{∙ (6 + 4) − 𝑀 = 0;
∑𝑚}𝐶 ^{= −𝑀}𝐴 ^{− 𝑌}𝐴^{∙ 6 − 𝑞 ∙ 8 ∙ 12 − 𝑃}2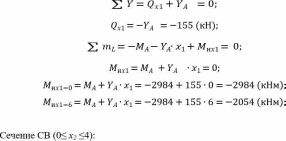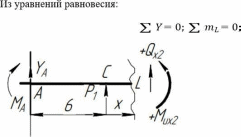<sup>∙ 4 − 𝑀 = 0;










∑ 𝑌 = 𝑄</sup>𝑥2 ^{+ 𝑌}𝐴 ^{+ 𝑃}1 ^{= 0;
𝑄}𝑥2 ^{= −𝑌}𝐴^−𝑃1^{= −155 − 35 = −190 (кН);}

∑𝑚_L = −𝑀_𝐴 −Y_A∙ (6 + 𝑥₂) +𝑀_их2 − 𝑃₁· 𝑥₂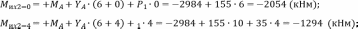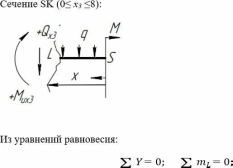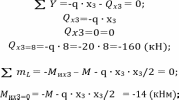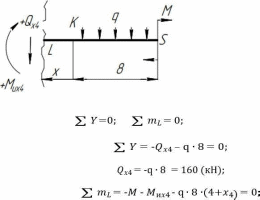