|
1 Математический анализ. Аn, то говорят, что задана числовая последовательность аn
Если по некоторому закону каждому натуральному числу поставлено в соответствие определенное число аn, то говорят, что задана числовая последовательность {аn}.
Число А называется пределом числовой последовательности {аn}, если для любого ε>0 найдется такой номер N, зависящий от ε, что для всех членов последовательности с номерами n>N верно неравенство
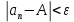
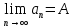
Число А называется пределом функции y=f(x) при х→∞, если для любого ε>0 найдется также число S>0, зависящее от ε, что для всех х таких, что 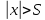 , будет верно неравенство , будет верно неравенство 
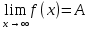
Число А называется пределом функции f(x) при х→х0, если для любого ε>0 найдется также число δ>0, зависящее от ε, что для всех х≠х0 и удовлетворяющих условию 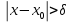 , будет выполняться неравенство , будет выполняться неравенство 
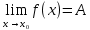
Функция α(х) называется бесконечно малой величиной при х→х0 (или х→∞), если 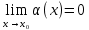 ( (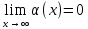 ) )
Функция f(x) называется бесконечно большой величиной при х→х0 , если для любого М>0 найдется также число δ>0, зависящее от М, что для всех х≠х0 и удовлетворяющих условию 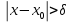 , будет выполняться неравенство , будет выполняться неравенство 

Свойства бесконечно малых величин:
- Если α(х) и β(х) – бесконечно малые величины при х→х0 (или х→∞), то будут бесконечно малыми величины: α(х) + β(х); α(х) - β(х); с∙ α(х), с – постоянная; f(x) ∙ α(х), f(x) – ограниченная функция; α(х) ∙ β(х); α(х) / f(х), 
Свойства бесконечно больших:
Если f(x) – бесконечно большая величина при х→х0 (или х→∞), то будут бесконечно большими величины: f(x) ∙ φ(x)  ; f(x) + φ(x), φ (x) – ограниченная функция; f(x) - φ(x), φ (x) – ограниченная функция; f(x) / φ(x), φ (x) – имеет предел ; f(x) + φ(x), φ (x) – ограниченная функция; f(x) - φ(x), φ (x) – ограниченная функция; f(x) / φ(x), φ (x) – имеет предел
Если функция α(х) есть бесконечно малая величина при х→х0 (или х→∞), то функция 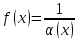 является бесконечно большой, и обратно, если f(x) бесконечно большая функция при х→х0 (или х→∞), то является бесконечно большой, и обратно, если f(x) бесконечно большая функция при х→х0 (или х→∞), то 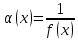 является бесконечно малой величиной является бесконечно малой величиной
Сравнение порядков бесконечно малых
Если α(х) и β(х) – бесконечно малые величины при х→х0 (или х→∞) и 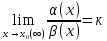
то при к=0 бесконечно малая α(х) называется бесконечно малой более высокого порядка малости, чем β(х)
при 0<к<∞ - одного порядка малости
при к=∞ - более низкого порядка малости, чем β(х).
Если к=1, то бесконечно малые α(х) и β(х) называются эквивалентными: α(х) β(х)
Примеры эквивалентно бесконечно малых величин при х→0: sin x
x, ex-1
x, ln(1+x)
x, (1+x)m
1+mx, arcsin x
x, arctg x
x, 1 – cos x
x2/2
Предел отношения двух бесконечно малых величин не изменится, если эти бесконечно малые заменить им эквивалентными
Теоремы о пределах:
 , С – постоянная , С – постоянная
Если 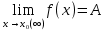 , , 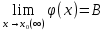 , то , то 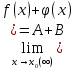 ; ; 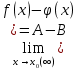 ; ; 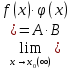 ; ;  , В≠0 , В≠0
Если  , , 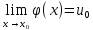 , то , то 
Первый замечательный предел 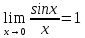
Второй замечательный предел (число е) 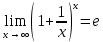
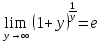
Для того чтобы найти предел элементарной функции, когда аргумент стремиться к значению, принадлежащему области определения этой функции, нужно в выражение функции вместо аргумента подставить его предельное значение.
Однако, далеко не всякая подстановка предельного значения в функцию вместо независимой переменной может сразу привести к нахождению предела.
Случаи, в которых подстановка предельного значения в функцию не дает значения предела, называют неопределенностями; к ним относятся неопределенности видов
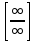 , , 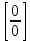 , ,  , ,  , ,  , , 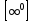 , , 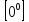
Устранить неопределенность удается часто с помощью алгебраических преобразований.
1-й тип.
Рассмотрим примеры вида  с неопределенностью вида с неопределенностью вида 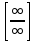 , где f(x) и φ(x) – сложные степенные или показательные функции. , где f(x) и φ(x) – сложные степенные или показательные функции.
В случае степенных функций необходимо выносить за скобку в числителе и знаменателе дроби х с наибольшим показателем степени среди всех слагаемых дроби; в случае показательных функций за скобку выносится наиболее быстро возрастающее слагаемое среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется.
2-й тип.
Рассмотрим примеры вида  с неопределенностью вида с неопределенностью вида 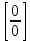 . .
В этом случае необходимо разложить на множители и числитель, и знаменатель дроби или домножить и числитель, и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.
3-й тип.
Рассмотрим примеры с неопределенностью вида  . .
Если функция, стоящая под знаком предела, представляет собой алгебраическую сумму дробей, то неопределенность устраняется или приводится ко 2-ому типу после приведения дробей к общему знаменателю. Если функция, стоящая под знаком предела, представляет собой алгебраическую сумму иррациональных выражений, то неопределенность или устраняется, или приводится к 1-му путем домножения и деления функции на одно и то же выражение, приводящее к формулам сокращенного умножения.
4-й тип.
Рассмотрим примеры с неопределенностью вида  . В этом случае выражение, стоящее под знаком предела, представляет собой степенно-показательную функцию. В основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи выделения «второго замечательного предела». . В этом случае выражение, стоящее под знаком предела, представляет собой степенно-показательную функцию. В основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи выделения «второго замечательного предела».
5-й тип.
К этому типу отнесем функции, сводящиеся к первому замечательному пределу: 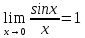
Эффективным средством вычисления пределов является применение эквивалентных бесконечно малых. Данный способ основан на том, что предел отношения двух бесконечно малых величин не изменится, если эти бесконечно малые заменить им эквивалентными.
Изучить и законспектировать самостоятельно тему «Непрерывность функции и точки разрыва»
Литература:
- Письменный Д. Т.Конспект лекций по высшей математике, часть 1, параграф 19, стр. 130-136
- Высшая математика для экономистов, под ред. Н. Ш. Кремера, глава 6, часть 6.7, стр. 161-165.
В наше время никакой прогноз развития какой либо реальной социально-экономической системы без применения математики уже не считается научно обоснованным, никакое предложение, касающееся управления такой системой, без его предварительно проведенного всестороннего математического анализа не воспринимается как серьезное – так как последствия управления должны соответствовать желаемым!
Накопленный человечеством опыт свидетельствует, что именно математика, помимо того, что содержит в себе мощный инструментарий для проведения количественных расчетов и решения прикладных задач самой разной природы, также является универсальным языком науки, образцом исследования четко поставленных проблем.
В соответствии с программой курса «Математика» предусмотрено изучение нескольких базовых разделов математики. Усвоение этих разделов необходимо чтобы, во-первых, правильно воспринимать другие нормативные и выборочные учебные дисциплины и, во-вторых, понимать постановки, методы исследования и методы решения типичных задач, возникающих в будущей профессиональной деятельности.
Математический анализ
Дискретная математика и математическая логика |
|
|
 Скачать 47.3 Kb.
Скачать 47.3 Kb.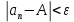
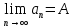
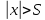 , будет верно неравенство
, будет верно неравенство 
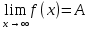
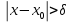 , будет выполняться неравенство
, будет выполняться неравенство 
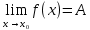
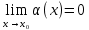 (
(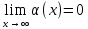 )
)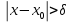 , будет выполняться неравенство
, будет выполняться неравенство 


 ; f(x) + φ(x), φ (x) – ограниченная функция; f(x) - φ(x), φ (x) – ограниченная функция; f(x) / φ(x), φ (x) – имеет предел
; f(x) + φ(x), φ (x) – ограниченная функция; f(x) - φ(x), φ (x) – ограниченная функция; f(x) / φ(x), φ (x) – имеет предел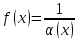 является бесконечно большой, и обратно, если f(x) бесконечно большая функция при х→х0 (или х→∞), то
является бесконечно большой, и обратно, если f(x) бесконечно большая функция при х→х0 (или х→∞), то 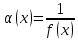 является бесконечно малой величиной
является бесконечно малой величиной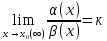

 , С – постоянная
, С – постоянная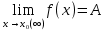 ,
, 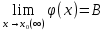 , то
, то 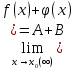 ;
; 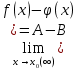 ;
; 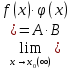 ;
;  , В≠0
, В≠0 ,
, 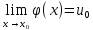 , то
, то 
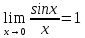
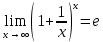
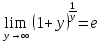
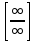 ,
, 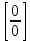 ,
,  ,
,  ,
,  ,
, 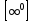 ,
, 
 с неопределенностью вида
с неопределенностью вида  с неопределенностью вида
с неопределенностью вида