отчет тарасова (1). Анализ инвестиционной привлекательности регионов и отраслей народного хозяйства в ms excel
 Скачать 385.28 Kb. Скачать 385.28 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Федеральное государственное бюджетное образовательное учреждение высшего образования «Уральский государственный университет путей сообщения» (ФГБОУ ВО УрГУПС) Факультет: Экономики и управления Кафедра: «Экономика транспорта» Отчет по дисциплине: Экономическая оценка инвестиций и управление проектами Тема: Анализ инвестиционной привлекательности регионов и отраслей народного хозяйства в MS EXCEL
Екатеринбург 2021 Регрессионный и корреляционный анализ – статистические методы исследования. Эти методы актуальны и на данный момент. Они необходимы для того, чтобы показать зависимость какого-либо параметра от одной или нескольких независимых переменных. Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения. Прежде чем говорить о количественной оценке результатов модернизации строительства, необходимо выполнить корреляционно-регрессионный анализ, который устанавливает связь между объемом инвестиций в строительство и числом действующих строительных организаций. Для установления зависимости переменных используется корреляционный анализ, а для выявления тренда данной зависимости проведен регрессионный анализ. Задачи корреляционно-регрессионного анализа включают установление формы зависимости между переменными, оценку функции регрессии, проверку достоверности построенной функции регрессии. В зависимости от количества факторов (независимых переменных), оказывающих влияние на зависимую переменную, корреляционно-регрессионный анализ можно классифицировать на парный и множественный. Основной гипотезой является то, что с увеличением числа строительных организаций, возрастает объём инвестиций в строительство, что приведет к увеличению числа организаций. Для установления зависимости переменных используется корреляционный анализ, а для выявления тренда данной зависимости проведен регрессионный анализ. Задачи корреляционно-регрессионного анализа включают установление формы зависимости между переменными, оценку функции регрессии, проверку достоверности построенной функции регрессии. Применяется парный корреляционно- регрессионный анализ, который позволяет определить зависимость между числом действ строительных организаций X (шт) и объёмом инвестиций в строительство Y (млн. руб.) за период, равный 10 годам. На основе данных аналитической группировки, полученных с сайта Росстат (таблица 1), построим эмпирическую линию связи (линию регрессии), вид которой позволит судить о возможном наличии связи и даст представление о форме корреляционной связи. Таблица 1 - Исходные данные для корреляционно-регрессионного анализа
У меня в качестве (У) выступает объём инвестиций в строительство, (Х)- число действ строительных организаций Уравнение регрессии предполагает наличие линейной статистической зависимости между числом действующих строительных организаций X и объемом инвестиций в строительство Y. Для определения степени тесноты парной линейной зависимости используем линейный коэффициент корреляции. 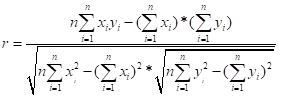 Одной из основных задач парного регрессионного анализа является установление вида функции регрессии . Значение коэффициента корреляции Пирсона лежит в интервале [–1; 1]. Чем больше абсолютное значение коэффициента, тем сильнее связаны переменные. Согласно принципу минимальной сложности для зависимости вели-чины действующих организаций от объема инвестиций была выбрана ли-нейная модель регрессии, которая имеет вид: (x) = a + bх , где a – свободный член (const); b – коэффициент регрессии (угловой коэффициент). Параметры уравнения определены с помощью метода наименьших квадратов (МНК), то есть найдены такие параметры модели, при которых сумма квадратов отклонений эмпирических (фактических) значений результирующего признака от теоретических, полученных по выбранному уравнению регрессии, будет стремиться к минимуму, то есть: 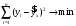 где yi – фактическое значение признака; ŷx – теоретическое значение результативного признака, найденное исходя из уравнения регрессии ((x)). Для определения коэффициентов a и b линейной регрессии решается следующая система нормальных уравнений: 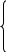  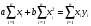 . .По результатам вычислений значения коэффициентов регрессии: a = 165487,7306 b = 0,033804309 Тогда уравнение парной регрессии для исследуемой зависимости следующее: f(x) =165487,7306 + 0,033804309*х. Для оценки адекватности уравнения регрессии был использован коэффициент детерминации R2, который показывает, какая доля вариации зависимой переменной обусловлена вариацией объясняющей переменной. Вычисляется коэффициент детерминации по формуле: 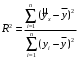  К Оценка значимости уравнения регрессии в целом производится на основе F-критерия Фишера. Фактическое значение F-критерия Фишера можно рассчитать по формуле: 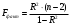 Фактическое значение F-критерия Фишера сравнивается с табличным значением. Если |tрасч|≥ tтабл, то коэффициенты регрессии признаются значимыми. Итоги корреляционно-регрессионного анализа представлены в таблице 2. Графически исследуемая зависимость величины объема инвестиций от числа организаций на рисунке 1. Рисунок 1 - Уравнение регрессии число организаций X на объема инвестиций Y 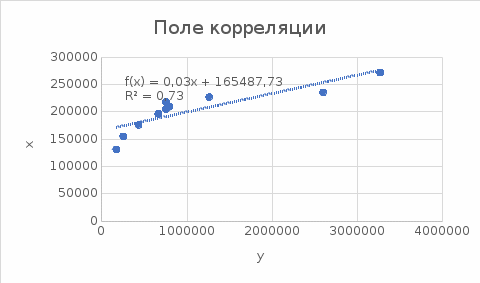 Линия тренда линейной регрессии представляет модель среднестатистической деградации технического состояния строительства. На графике две зоны, которые можно интерпретировать как зону «удовлетворительного состояния» (находится ниже линии тренда) и зону «неудовлетворительного состояния» (находится выше линии тренда). Таким образом, накладывая на график параметры величины объема инвестиций и числа организаций, можно судить о состоянии строительства. Таблица 2 - Итоги корреляционно-регрессионного анализа  В первую очередь обращаем внимание на R-квадрат и коэффициенты. R-квадрат – коэффициент детерминации. В моём примере 0,733, или 73,3%. Это означает, что расчетные параметры модели на 73,3% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо». То есть чем выше значение коэффициента детерминации, тем выбранная модель считается более применимой для конкретной задачи. Если F-статистика, называемая также критерием Фишера, используется для оценки значимости линейной зависимости, опровергая или подтверждая гипотезу о ее существовании. Коэффициент 165487,73 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели. Значение t-статистики (критерий Стьюдента) помогает оценивать значимость коэффициента при неизвестной либо свободного члена линейной зависимости. Если значение t-критерия > tкр, то гипотеза о незначимости свободного члена линейного уравнения отвергается. Коэффициент 0,0338 показывает весомость переменной Х на Y. То есть ущерб в пределах данной модели влияет на степень износа с весом 0,0338. Знак «+» указывает на положительное влияние: чем больше число строительных организаций, тем больше объём инвестиций. Ось линии статистической связи между фактором и результативным признаком, судя по модулю коэффициента корреляции, в соответствии со шкалой Чэддока тесная. Таким образом, проведенный анализ доказывает с вероятностью 95 %, что объем инвестиций в строительство существенно влияет на число действующих строительных организаций. Замена переменных X и Y. Таблица 3 - Исходные данные для корреляционно-регрессионного анализа)
Уравнение регрессии предполагает наличие линейной статистической зависимости между объемом инвестиций в строительство Y и числом действующих строительных организаций X. Для определения степени тесноты парной линейной зависимости используем линейный коэффициент корреляции. Для определения коэффициентов a и b линейной регрессии решается следующая система нормальных уравнений: 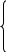 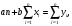 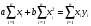 . .По результатам вычислений значения коэффициентов регрессии: a = -3295188; b = 21,67622. Тогда уравнение парной регрессии для исследуемой зависимости следующее: f(x) =-3295188+ 21,67622*х. Таблица 3 - Итоги корреляционно-регрессионного анализа  R-квадрат – коэффициент детерминации. У меня 0,733, или 73,3%. Это означает, что расчетные параметры модели на 73,3% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо». То есть чем выше значение коэффициента детерминации, тем выбранная модель считается более применимой для конкретной задачи. Если F-статистика, называемая также критерием Фишера, используется для оценки значимости линейной зависимости, опровергая или подтверждая гипотезу о ее существовании. Коэффициент -3295188 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели. Значение t-статистики (критерий Стьюдента) помогает оценивать значимость коэффициента при неизвестной либо свободного члена линейной зависимости. Если значение t-критерия > tкр, то гипотеза о незначимости свободного члена линейного уравнения отвергается. Коэффициент 21,67622 показывает весомость переменной Х на Y. То есть ущерб в пределах данной модели влияет на степень износа с весом 21,67622. Знак «+» указывает на положительное влияние: чем больше число строительных организаций, тем больше объём инвестиций. Ось линии статистической связи между фактором и результативным признаком, судя по модулю коэффициента корреляции, в соответствии со шкалой Чэддока тесная. Таким образом, проведенный анализ доказывает с вероятностью 95 %, что объем инвестиций в строительство существенно влияет на число действующих строительных организаций. Рисунок 2 - Уравнение регрессии объем инвестиций Y на числа организаций X 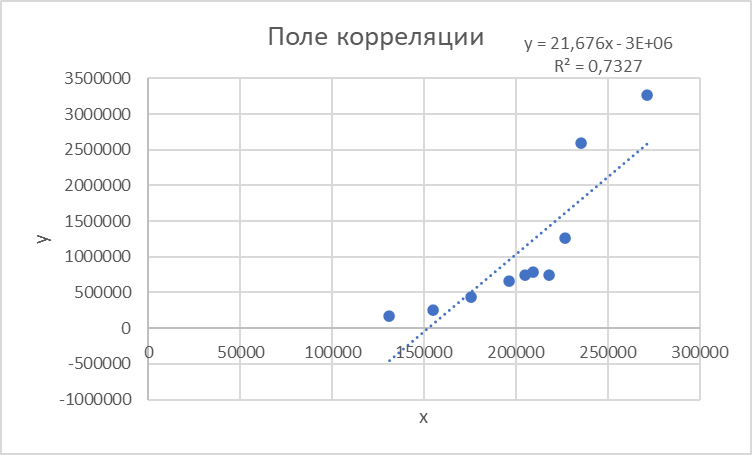 Заключение По проведённой работе я могу сделать вывод, что процесс модернизации является процессом необходимым и закономерным для повышения конкурентоспособности строительства, а значит, и методика расчета экономической эффективности данного процесса требует развития существующих методических подходов. Применение математических моделей позволит более точно оценить экономический эффект от внедрения определенных результатов современных разработок в практическое применение. Основная задача математического моделирования надежности и достоверности – это формирование математических моделей, адекватных вероятностным процессам функционирования исследуемых реальных технических систем. Исследование этих моделей позволяет выработать конкретные рекомендации по повышению надежности и достоверности полученной информации, необходимой для принятия управленческого решения в области внедрения современных технических разработок, т. е. приводит к разработке методов анализа и синтеза этих систем. Эффективность использования математических методов анализа и синтеза на этапах проектирования, разработки и эксплуатации, определяется сложностью используемой системы. Поэтому чем более сложным является принцип организации системы (структура соединения элементов, взаимосвязь при функционировании, характер технического обслуживания и материального обеспечения и т. д.), тем более сложной она должна быть. Хочется отметить, что понятия «корреляция» и «регрессии» тесно связаны между собой. В экономических исследованиях корреляционный и регрессионный анализ нередко объединяют в один – корреляционно-регрессионный анализ. Подразумевается, что в результате такого анализа будет построена регрессионная зависимость и рассчитаны коэффициенты ее тесноты и значимости (т.е. проведен корреляционный анализ). Список используемых источников. http://gks.ru/bgd/regl/B08_11/IssWWW.exe/Stg/d03/24-08-2.htm http://gks.ru/bgd/regl/b09_11/IssWWW.exe/Stg/d03/24-07.htm http://gks.ru/bgd/regl/b12_11/IssWWW.exe/Stg/d2/24-07.htm http://gks.ru/bgd/regl/b14_11/IssWWW.exe/Stg/d02/24-07.htm http://gks.ru/bgd/regl/b17_11/Main.htm 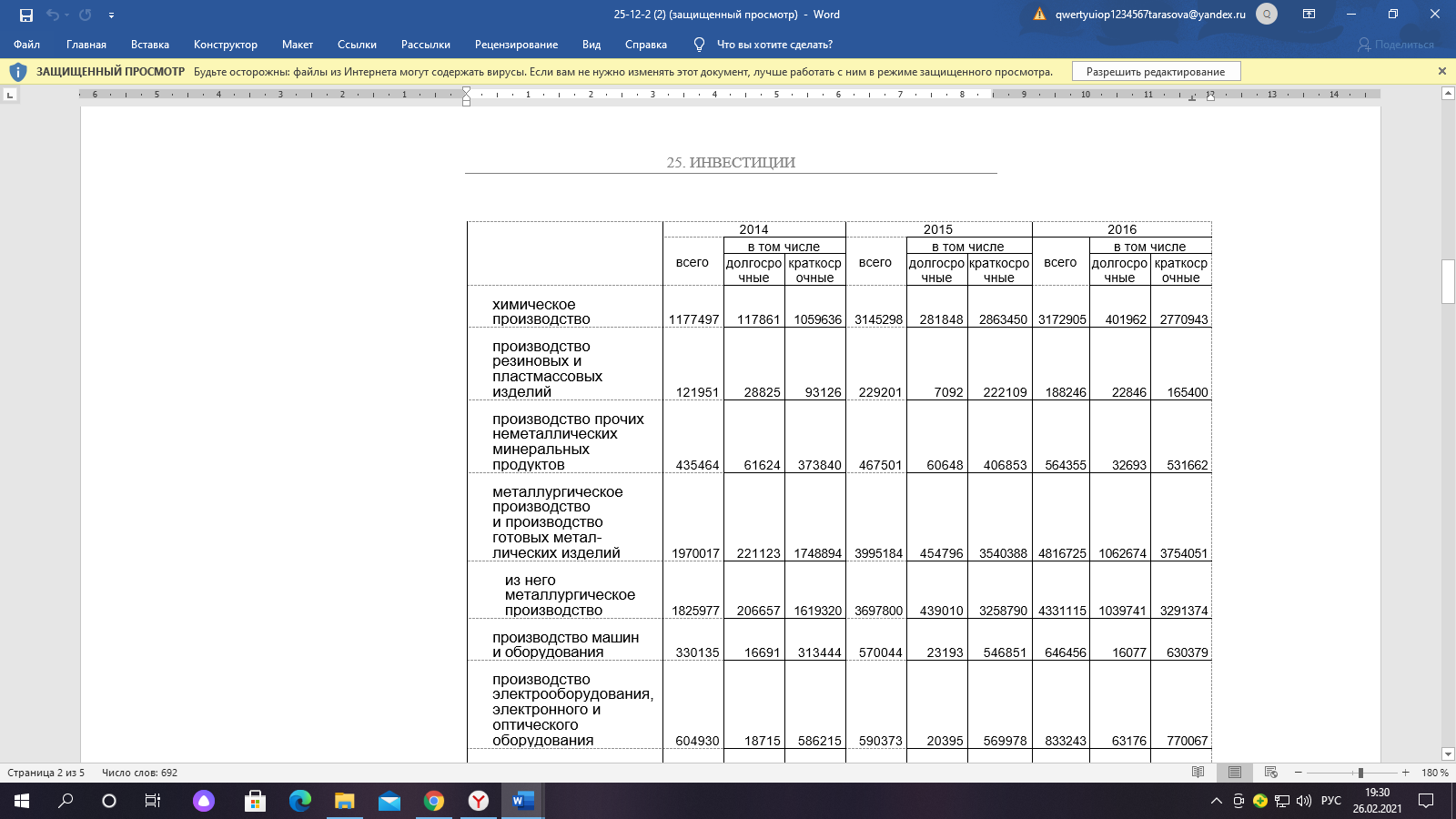 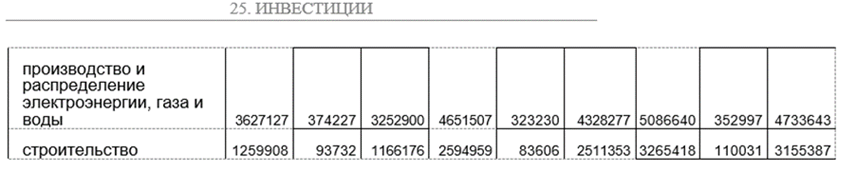 https://gks.ru/bgd/regl/b10_13/IssWWW.exe/Stg/d4/16-04.htm https://gks.ru/bgd/regl/b11_13/IssWWW.exe/Stg/d4/16-04.htmъ https://gks.ru/bgd/regl/b12_13/IssWWW.exe/Stg/d4/16-04.htm https://gks.ru/bgd/regl/b13_13/IssWWW.exe/Stg/d3/16-04.htm https://gks.ru/bgd/regl/b14_13/IssWWW.exe/Stg/d03/17-04.htm https://gks.ru/bgd/regl/b15_13/IssWWW.exe/Stg/d03/17-04.doc https://gks.ru/bgd/regl/b16_13/IssWWW.exe/Stg/d03/17-04.doc https://gks.ru/bgd/regl/b17_13/IssWWW.exe/Stg/d02/18-01-07.doc |
