Анализ результатов егэ за 2013 год
 Скачать 372.53 Kb. Скачать 372.53 Kb.
|
Задание С3Задание С3 относится к высокому уровню сложности. В данном проверяется умение строить дерево игры по заданному алгоритму и обосновывать выигрышную стратегию [15]. Теоретический материал для решения задания С3Теория игр — математический метод изучения оптимальных стратегий в играх. Под игрой понимается процесс, в котором участвуют две и более сторон, ведущих борьбу за реализацию своих интересов. Каждая из сторон имеет свою цель и использует некоторую стратегию, которая может вести к выигрышу или проигрышу — в зависимости от поведения других игроков. Стратегия игрока в игре – это полный план действий при всевозможных ситуациях, способных возникнуть. Стратегия определяет действие игрока в любой момент игры и для каждого возможного течения игры, способного привести к каждой ситуации. Дерево — это связный ациклический граф. Связность означает наличие путей между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути. Построить дерево игры – это значит рассмотреть для каждой позиции игры все возможные ходы игроков до тех пор, пока позиция не окажется выигрышной. Разбор задания С3Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в три раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 45 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 47. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 47 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤46. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. Выполните следующие задания. Во всех случаях обосновывайте свой ответ. 1. а) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S. б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани. 2. Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём (а) Петя не может выиграть за один ход и (б) Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для каждого указанного значения S опишите выигрышную стратегию Пети. 3. Укажите значение S, при котором: – у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и – у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход; в узлах — количество камней в куче [5]. Суть игры описана подробно, поэтому можно сразу переходить к заданиям и строить дерево игры. а) Все значения S, при которых Петя выиграет в один ход находятся в промежутке от 16 до 46 включительно. Увеличив любое из этих чисел в три раза Петя выиграет в один ход, получив больше 47 камней. б) Из пункта 1 а) следует, что все значения при которых Петя не сможет выиграть в один ход находятся в промежутке от 1 до 15 включительно. Для того, чтобы при любом ходе Пети первым ходом выиграл Ваня, утроив полученное число, S изначально должно быть равно 15. В этом случае дерево игры может выглядеть следующим образом: 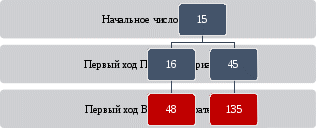 Для того, чтобы Петя гарантированно выиграл вторым ходом, независимо от того, как будет ходить Ваня, нужно, чтобы после первого хода Пети число камней в куче стало 15. После очередного хода Вани, Петя выиграет утроив число камней в куче. То есть изначально в куче должно быть 14 или 5 камней. В этом случае дерево игры может выглядеть следующим образом: 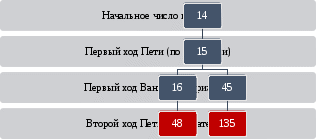 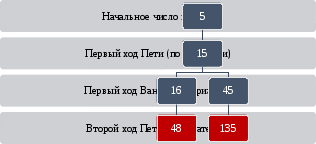 Ваня сможет гарантированно выиграть вторым ходом, если после хода Пети камней в куче будет 14. Соответственно, начальное количество камней в куче должно быть 13 для того, чтобы Петя своим первым ходом увеличил их либо до 14, либо до 39. Дальнейшие действия (для 14) описаны в п.2, а при 39 Ваня выиграет, увеличив число камней в куче в 3 раза. В этом случае дерево игры может выглядеть следующим образом: 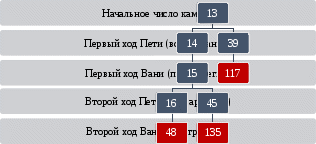 Рекомендации к решению заданий С3Для решения этого задания необходимо понимать, что представляет собой игра и правильно построить дерево игры. Решить задание – значит грамотно ответить на вопросы, которые расположены в порядке увеличения сложности. При ответе на каждый вопрос нужно показать, что число камней в куче найдено верно и объяснить почему та или иная позиция является проигрышной или выигрышной для каждого игрока. Нужно указать все возможные проигрышные ходы для того, чтобы убедиться, что выигрышный ход найден верно. Важно не перепутать порядок игроков. Каждый ответ должен быть обоснован. В этом задании при оценки не учитываются арифметические ошибки [14]. |
