Практическое задание 2
Проанализируйте данные зависимости успеваемости (балл в сессию) магистрантов группы ЭКмз-1501 в весеннюю сессию 2015–2016 учебного года по курсу «Статистика» от пропущенных ими занятий во 2-ом семестре (таблица 1). Изобразите графически зависимость успеваемости магистрантов, предварительно проранжировав значения х в порядке возрастания.
Таблица 1
Данные по магистрантам
Номер магистранта
|
Балл в сессию, у
|
Количество пропущенных занятий, х
|
1
|
5
|
1
|
2
|
3
|
8
|
3
|
4
|
3
|
4
|
4
|
5
|
5
|
3
|
8
|
6
|
2
|
10
|
7
|
5
|
2
|
8
|
4
|
4
|
9
|
5
|
2
|
10
|
3
|
6
|
Решение:
Факторный (независимый) признак х – количество пропущенных занятий. результативный (зависимый) признак у – балл в сессию. Выдвигаем гипотезу о том, что между количеством пропущенных занятий и баллом в сессию существует корреляционная зависимость.
Ранжируем данные в порядке возрастания фактора Х - количество пропущенных занятий (таблица 2) и получаем два параллельных ряда.
Графически зависимость между признаками изображаем в виде поля корреляции (рисунок 1).
Вывод. Сравнивая значения количества пропущенных занятий и баллом в сессию (таблица 2) можно заметить, что с увеличением количества пропущенных занятий практически по каждому магистранту происходит снижение балла в сессию. Это говорит о наличии обратной корреляционной связи между признаками.
Распределение облака точек на поле корреляции (рисунок 1) произошло из левого верхнего угла в правый нижний угол. Это подтверждает обратную корреляционную связь между признаками, т.е. с увеличением количества пропущенных занятий балл успеваемости в среднем снижается. По форме связи можно предположить линейную зависимость.
Таблица 2
Параллельные ряды
Номер магистранта
|
Количество пропущенных занятий,
х
|
Балл в сессию,
у
|
1
|
1
|
5
|
7
|
2
|
5
|
9
|
2
|
5
|
3
|
3
|
4
|
8
|
4
|
4
|
4
|
5
|
4
|
10
|
6
|
3
|
2
|
8
|
3
|
5
|
8
|
3
|
6
|
10
|
2
|
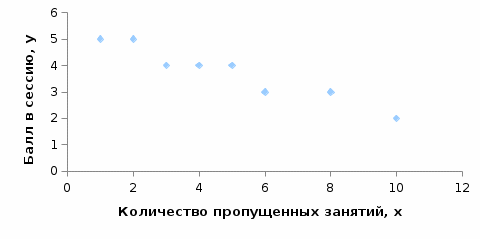
Рисунок 1 – Поле корреляции
| |
 Скачать 20.87 Kb.
Скачать 20.87 Kb.