Аппроксимация данных методом наименьших квадратов - Иванов. Аппроксимация данных методом наименьших квадратов

• Название: Аппроксимация данных методом наименьших квадратов
• Дата: 30.10.2022
• Размер: 1.15 Mb.
• Имя файла: Аппроксимация данных методом наименьших квадратов - Иванов.docx
• Тип: Реферат; #762618

Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования


РЕФЕРАТ


по дисциплине «Научно-исследовательский семинар»
на тему: «Аппроксимация данных методом
наименьших квадратов»


Студент гр. 2801б………………...……… /Иванов С.О./
Преподаватель (доц.)..………………………/Гришин С.Н./


Оценка:…………………….
Дата: ……………………..
Подписи: …………………..








Ханты-Мансийск
2022


Оглавление

Аппроксимация. Постановка задачи 2

Метод наименьших квадратов 6

Список литературы 11

Аппроксимация. Постановка задачи

Аппроксимация – построение приближённой функции, наиболее близко проходящей около данных точек или около данной непрерывной функции. Такая задача возникает, когда в исходных данных существует погрешность или желательно упростить сложную математическую зависимость.

В практике известны 3 способа задания функции: аналитический, графический, табличный. В инженерной практике наиболее распространенным является случай, когда вид связи между параметрами X и Y неизвестен, т.е. невозможно записать эту связь в виде некоторой зависимости y = f(x). Как правило, даже при известной зависимости y = f(x), она настолько громоздка, что ее использование в практических расчетах затруднительно. Чаще всего эта связь представлена в виде таблицы, т.е. дискретному множеству значений аргумента {xi} поставлено в соответствие множество значений функции {yi}(i = 1, 2, .., п). Эти значения – либо результаты расчетов, либо экспериментальные данные.

На практике нам могут понадобиться значения величины y и в других точках, отличных от узлов xi . Часто эти значения можно получить лишь путем сложных расчетов или проведением дорогостоящих экспериментов. Таким образом, необходимо использовать имеющиеся табличные данные для приближенного вычисления искомого параметра y при любом значении (из некоторой области) определяющего параметра х, поскольку точная связь y = f(x) неизвестна. Задачи исследования в большинстве случаев требуют установить определенный вид функциональной зависимости между характеристиками изучаемого явления. Этой цели и служит задача о приближении функции. Т.е. задача о приближении (аппроксимации) функции состоит в том, чтобы данную функцию f(x) приближенно заменить (аппроксимировать) некоторой функцией φ(х), значения которой в заданной области мало отличались от опытных данных – f(x) ≈ φ(х). Методы решения такой задачи относятся к категории численных методов или методов вычислительной математики. Один из способов аппроксимации функций – интерполяция. Он используется в тех случаях, когда основная информация о приближаемой функции дается в виде таблицы ее значений. В результате решения задачи интерполяции линия, соответствующая интерполирующей функции, будет обязательно проходить через все точки исходных данных. В этом случае точки являются узлами интерполяции.

При интерполяции от приближения требуется, чтобы оно имело ту же таблицу значений, что и приближаемая функция:

φ(хi) = f(xi), i = 0, 1, 2, …, n.

Это условие называется условием интерполяции. Функция, удовлетворяющая условиям интерполяции, называется интерполяционной, а точки х0, х1, х2, …, хп - узлами интерполяции.

Чаще всего в качестве интерполяционных функций выбирают алгебраические многочлены, так как их значения вычисляются проще всего. Таким образом, решается следующая задача определяется алгебраический многочлен n-й степени:



удовлетворяющий условиям интерполяции:

Р_п(x_i) = f(x_i), i = 0, 1, 2, …, n.

Алгебраический многочлен, удовлетворяющий этим условиям, называется интерполяционным многочленом. Геометрический смысл интерполяции состоит в том, что графики функции у = f(x) и интерполяционного многочлена у = Р_п(x) должны проходить через все табличные точки (x_i , у_i), i = 0, 1, 2,…, n. На рис. 1, а эти точки выделены. Именно это условие должно обеспечить близость графиков этих функций на рассматриваемом отрезке, чтобы можно было использовать интерполяционный многочлен Pn(x) в качестве приближения для функции f(x). Кроме построения интерполяционных зависимостей, можно использовать более общий вариант приближения функции – построение аппроксимирующих зависимостей на основе различных функциональных взаимосвязей между двумя рассматриваемыми величинами. Приближенная функциональная зависимость, полученная на основании экспериментальных данных, называется аппроксимирующей функцией или эмпирической формулой.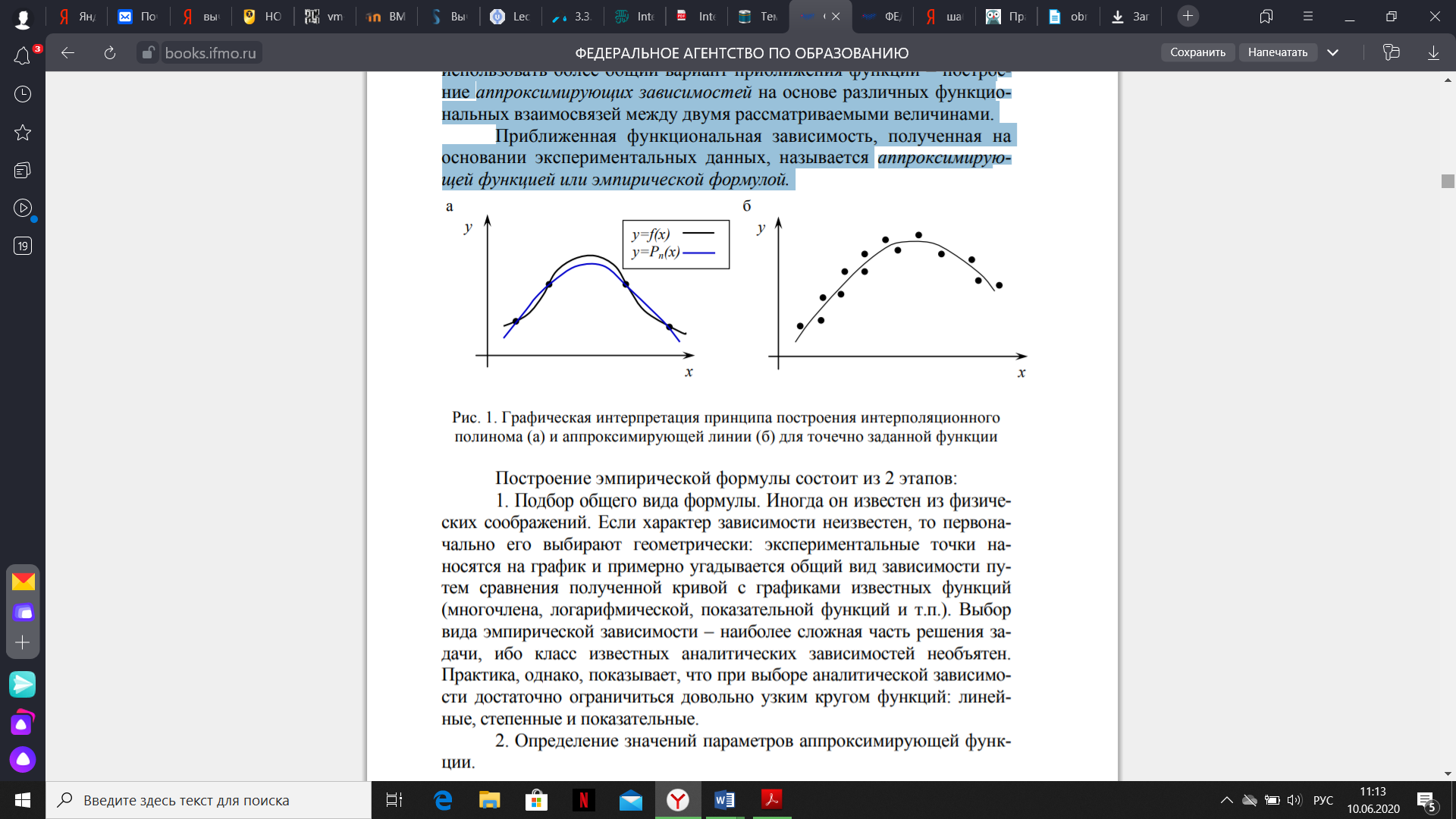



Построение эмпирической формулы состоит из 2 этапов:

1. Подбор общего вида формулы. Иногда он известен из физических соображений. Если характер зависимости неизвестен, то первоначально его выбирают геометрически: экспериментальные точки наносятся на график и примерно угадывается общий вид зависимости путем сравнения полученной кривой с графиками известных функций (многочлена, логарифмической, показательной функций и т.п.). Выбор вида эмпирической зависимости – наиболее сложная часть решения задачи, ибо класс известных аналитических зависимостей необъятен. Практика, однако, показывает, что при выборе аналитической зависимости достаточно ограничиться довольно узким кругом функций: линейные, степенные и показательные.

2. Определение значений параметров аппроксимирующей функции.
Метод наименьших квадратов


Ранее были рассмотрены две задачи восстановления функциональных зависимостей: первая – вычисление значений трансцендентных функций, вторая – интерполяция. Решения обеих этих задач представлялись в виде алгебраического многочлена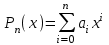

. (1)

Исходными данными для определения коэффициентов многочлена в первом случае были значения производных разных порядков, заданных в какой-то одной точке, а во втором случае значения самой функции, заданные в нескольких точках.

При решении задачи аппроксимации также задаются значения функции в разных точках в виде таблицы x_j, y_j, j=1,…,m. Однако в этом случае считается, что значения функции содержат значительную долю случайной погрешности. Самих значений задается, как правило, больше, чем при решении задачи интерполяции (рис.1). Поэтому в результате решения задачи аппроксимации полученная функция может не пройти ни через одну из заданных точек. Она должна пройти между ними наилучшим (в каком-либо смысле) образом.

Очевидно, что решать задачу интерполяции в случае, рассмотренном на рис.1, не имеет смысла.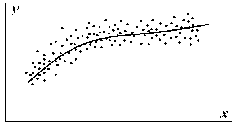


Рис. 1. К задаче аппроксимации функций
Переходим к математической постановке задачи. Для этого нужно математически определить критерий качества аппроксимации. Один из подходов к формированию критерия качества сводится к построению так называемой функции штрафа.

В начале необходимо решить, что является нарушением, которое может вызвать штрафование, и от чего зависит размер штрафа. Очевидно, что в данной задаче нарушением может быть непрохождение кривой, соответствующей аппроксимирующей функции, через одну из заданных точек. Причем, можно считать, что эти нарушения независимы, т.е. величины штрафов, накладываемые за каждое из нарушений в отдельности, не зависят друг от друга. Отсюда следует первый важный вывод, что функцию штрафа следует искать в виде суммы штрафов за каждое отдельное нарушение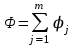

.

Остается найти вид функции локального штрафа. Нужно решить от какого параметра зависит величина штрафа. На этот вопрос ответить легко, поскольку взаимное расположение кривой и точки удобнее всего характеризовать расстоянием по оси ординат, то есть .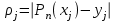

Теперь перейдем к построению зависимости 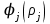, т.е. локальных штрафов.

При этом необходимо учитывать два условия:

- задача, которая получится в результате нашего выбора, должна иметь достаточно простое решение;

- полученное решение должно быть разумным с общей точки зрения, (например, кривая не должна проходить вне всей группы точек и т.п.).

В связи с этим поиск подходящей функциональной зависимости следует начинать с наиболее простых. Самыми простыми являются зависимости вида y=const, y=x. Первая нас, очевидно, не устраивает. Попытаемся представить функцию локального штрафа в виде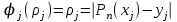

. (2)

Проанализируем последствия этого выбора.

Во–первых, наличие абсолютной величины в зависимости (2) приводит к ее негладкости (разрыву первой производной). Поэтому для минимизации штрафа невозможно применять методы, основанные на поиске стационарных точек 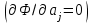. Это серьезно усложняет задачу.

Во вторых, рассмотрим ситуацию, изображенную на рис.2. Одному и тому же значению x=x_i=x_j соответствуют разные значения y_i и y_j. Такая ситуация очень часто случается при проведении повторных экспериментов с целью уменьшения влияния случайной составляющей погрешности. В данном случае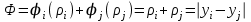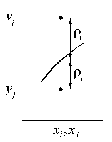

.


Рис. 2. Расположение кривой между точками
Таким образом, функция штрафа не зависит от положения кривой относительно этих двух точек. Мы пришли к некорректной задаче, что дополнительно осложняет ее решение. К тому же, исходя из здравого смысла, в этой ситуации наилучшим может быть только одно решение, когда кривая проходит точно посередине между двумя точками.

Значит, выбор 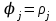следует отвергнуть.

Следующей по уровню сложности функциональной зависимостью является функция вида y=xx=x². Тогда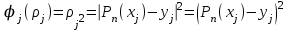

.

Данная функция является гладкой, и, следовательно, этот способ выбора _j(_j) не препятствует применению методов, связанных с дифференцированием.

Теперь найдем решение задачи в ситуации, показанной на рис.2.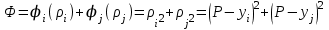

.

Продифференцируем это выражение по P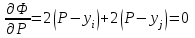

.

Отсюда имеем: 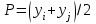, что соответствует решению, которое было получено из соображений здравого смысла.

В результате этого анализа мы приходим к заключению, что данный выбор удовлетворяет нашим требованиям.

Теперь окончательно сформулируем задачу в виде метода наименьших квадратов: минимизировать функцию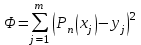

.

При этом значение Ф зависит только от значений коэффициентов многочлена (1), то есть Ф=Ф(a₀,a₁,…,a_n). Тогда с учетом (1)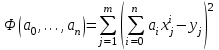

.

Для минимизации этой функции необходимо найти решение системы уравнений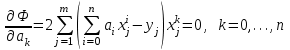

.

Преобразуем это выражение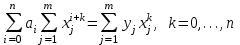

.

Эта система уравнений имеет вид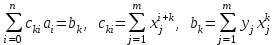

,

т. е. решение задачи методом наименьших квадратов сводится к решению системы линейных алгебраических уравнений.

Если число различных точек x_j m>n, то матрица системы не вырождена и решение системы существует и единственно. Это означает, что найденное решение доставляет функции Ф именно минимум, поскольку функция, имеющая вид суммы квадратов некоторых величин с положительными коэффициентами не может иметь единственной стационарной точки другого типа максимума.

При практическом применении метода наименьших квадратов степень многочлена n не следует выбирать слишком большой, так как это может привести к появлению осциллирующего характера у искомой функции P_n(x).

Поскольку, при постановке задачи предполагалось наличие значительной доли случайной погрешности (эта погрешность относится к погрешности исходных данных), то для оценки погрешности результата решения можно применить статистические способы, например, оценку среднеквадратичной погрешности .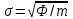

Список литературы

1. 
   Лекционный материал / Шерыхалина Н.М.
   
2. 
   Малышева Т.А. Численные методы и компьютерное моделирование. Лабораторный практикум по аппроксимации функций: Учеб.-метод. пособие. СПб.: Университет ИТМО, 2016. 33 с.
   
3. 
   http://libraryno.ru/3-3-approksimaciya-funkcii-matmodosipkina/